4.2: “Two Masses on a Spring” Model and Infrared (IR) Spectroscopy

Last updated
Save as PDF

Page ID: 398279

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

This Chapter presents a basic view of a classical physics model of “two masses on a spring” and shows how this model can help understand and interpret infrared (IR) spectroscopy data. This will be one of our examples of some theoretical foundation for a certain type of spectroscopy. This theory-experiment connection is important for every type of spectroscopy because spectroscopic data always need to be interpreted and it is not possible without a sufficiently accurate theory.

Learning Objectives

Understand the “mass on a spring” and “two masses on a spring” models and their capacity to predict the frequency of vibrations based on the mass and spring stiffness values
Develop an appreciation of the relationship between a model (“two masses on a spring”) and a physical process (“covalent bond atomic vibrations”)
Develop a sense how atomic masses and bond energy values define the resonance frequency (wavenumbers) in IR spectra

“One Mass on a Spring” Model

Figure IV.2.A shows an object of mass m attached to a massive wall via a classical spring of stiffness (spring force constant) k. In classical physics, the motion of the object is guided by the Newton’s 2nd law stating that an object of mass m moving under the influence of force F will be moving with acceleration such that: F= m•a. Based on Figure IV.2.A, we can apply tools of Calculus to calculate the trajectory, x(t), of the object.

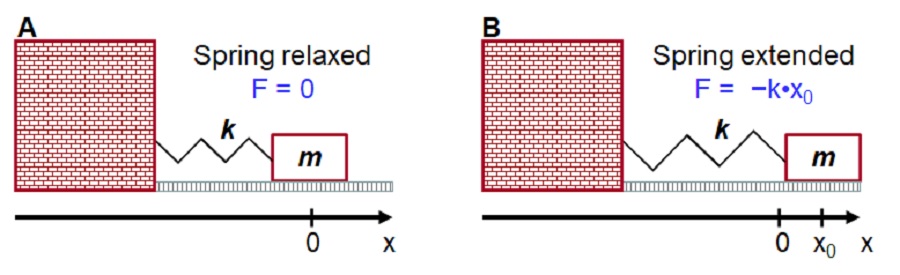
Figure_IV.2.A.jpg — Figure IV.2.A. “A mass on a spring” model. (A) a weightless spring of stiffness k connects an object of mass m to a wall of an infinitely large mass. The spring is initially relaxed (neither extended nor compressed) and thus it exerts zero force on the object of mass m. (B) The spring is extended by the initial value of x₀. The extended spring exerts initial force F=-k * x₀ on the object. Once the extended spring and mass are left alone, the system starts oscillatory motions driven by the force whose magnitude is directly proportional to the extension of the spring and direction is opposite to the spring compression or expansion. Equation IV.2.1 below describes the trajectory of the object of mass m.

The oscillation frequency \(\nu\) can be calculated from the Hooke’s law as a function of the object mass \(m\) and spring force constant \(k\) as follows:

\[\begin{eqnarray}F &=& -k \cdot x \\[4pt] m \cdot a &=& -k \cdot x \\[4pt] m \cdot \frac{d^2x}{d t^2} &=& -k \cdot x \\[4pt] x(t) &=& x_0 \cdot cos(\sqrt{\frac{k}{m}} \cdot t) \\\label{EQ:ms1}\end{eqnarray}\]

The obtained solution for the trajectory \(x(t)\) corresponds to a type of motion called harmonic oscillator (position depends on time as a cosine function). The mass on a spring model and its calculus-based treatment can be extended to any system, in which the restoring force is pulling in the direction opposite to the displacement from equilibrium and its absolute value is proportional to the displacement.

Big picture: The trajectory, x(t), of any system in which the absolute value of the restoring force is directly proportional to the value of the perturbation (displacement from equilibrium) and the direction of the restoring force is the opposite to the direction of the perturbation can be described by differential equations similar to Equation IV.2.3 above. For any such a system, its dynamics over time will be based on the harmonic oscillator model: x(t) = x₀⋅cos(ω ⋅ t). Moreover, for any system in which the second derivative of its coordinate is directly proportional to —coordinate, d²x/dt² = –ω²⋅x(t), the dynamics of its trajectory will be harmonic: x(t) = x₀⋅cos(ω⋅t + θ). In this equation, parameter ω defines the frequency of harmonic oscillations whereas parameters x₀ (initial amplitude or displacement) and θ (phase) are defined by the state of the system, x(t), at time t=0.

“Two Masses on a Spring” Model

Figure IV.2.B. Two masses connected by a compressible spring can undergo harmonic/oscillatory back-and-forth motions. Click on the image to see the action.

Two masses, m₁ and m₂, are connected by a spring with the force constant k (Figure IV.2.B). If the spring is compressed or extended and then let go, the two masses will be performing back-and-forth oscillatory motions.

The oscillation frequency ν can be calculated from the Hooke’s law as a function of reduced mass μ and spring force constant k as follows:

\[\begin{eqnarray}\nu &=& \frac{1}{2\pi} \cdot \sqrt{\frac{k}{\mu}} \\[4pt] \mu &=& \frac{m_1 \cdot m_2}{m_1 + m_2} \nonumber\label{EQ:mm2}\end{eqnarray}\]

The units of frequency is 1/s (the number of oscillations per second) or s^-1. This unit has a special name: Hertz or Hz.

Infrared (IR) Spectroscopy

Oscillations of two atoms connected by a covalent bond can be approximated by the model described with the “two masses on a spring” model shown above. The atoms have small but very specific mass values defined by the chemical type of the atoms corrected for their specific isotopic makeup (the number of neutrons). The bond energy values can be related to the stiffness of the spring (k value in equation IV.2.5 above).

Although this model lacks the capacity to describe some complicated cases, it is adequate to predict some trends in the IR signatures of a number of simple samples.

Infrared (IR) spectroscopy probes oscillations with wavelength values of 0.8 – 250 μm. The respective frequency values fall into the range of 1.20×10¹²– 3.75×10¹⁴ Hz. Note that the smallest frequency value corresponds to the longest wavelength and vice versa. This is because the irradiation wavelength λ (in meters) and oscillation frequency ν (in Hz or 1/sec) are inversely proportional via the speed of light constant c (300,000,000 m/s ):

\[\begin{eqnarray}\nu &=& c / \lambda \\\label{EQ:wf1}\end{eqnarray}\]

The characteristic oscillation frequency values measured by infrared spectroscopy are reported as so-called wavenumber, W, in units of cm^-1:

\[\begin{eqnarray}W &=& 1 / \lambda \\\label{EQ:wn1}\end{eqnarray}\]

Thus, the wavenumber values for the IR wavelengths (0.8 – 250 μm) cover the range 40-12,500 cm^-1.

Big picture: Infrared spectroscopy of small molecules allows calculation of the bond stiffness (k constant) for a great range of covalent bonds from the experimentally observed wavenumbers and atomic mass values known from the periodic table. The stiffness constant values obtained via such IR measurements then are used as bond stiffness parameters for the molecular dynamics force fields outlined in Chapter III.1 Potential Energy Surface and Bonding Interactions. Likewise, crystallographic structure of small molecules allow determination of the equilibrium covalent bond length and bond angle values, which are also used as corresponding force field parameters in molecular dynamics simulations.

IR Isotope Effect

Many types of atoms have several isotopic variants : ¹H, ²H and ³H for hydrogen, ¹²C and ¹³C for carbon etc. Isotopes of the same chemical type of an atom differ in the numbers of neutrons inside the nucleus: no (zero) neutrons in ¹H, one neutron in ²H and two neutrons in ³H. Therefore, the atomic mass values of isotopes of the same chemical type differ. This mass difference leads to different wavenumber values for IR bands when multiple isotopes of relevant atoms are present (the so-called IR “isotope effect”).

Examples

Example \(\PageIndex{1}\)

1. Two objects of 1.0 kg each are connected by a spring with stiffness value k = 5,000 N/m. What is the reduced mass μ of this system? What will be the frequency ν of free oscillations of this system if it gets excited and then left alone?

Answer: μ = 0.50 kg; ν = 15.9 Hz (oscillations per second)

Example \(\PageIndex{2}\)

2. Two objects of 4.0 kg each are connected by a spring with stiffness value k = 5,000 N/m. What is the reduced mass μ of this system? What will be the frequency ν of free oscillations of this system if it gets excited and then left alone?

Answer: μ = 2.0 kg; ν = 7.96 Hz

Note that quadrupling of both mass values (in comparison with problem 1 above) resulted in quadrupling of the reduced mass, which in turn resulted in decreasing by one-half of the oscillation frequency.

Practice Problems

Practice problem 1. Two objects of 1.0 kg each are connected by a spring with stiffness value k = 20,000 N/m. What is the reduced mass μ of this system? What will be the frequency ν of free oscillations of this system if it is excited and then left alone?

Practice problem 2. What is the approximate value of reduced mass μ on a system with one object having mass M much larger than the mass value m of the other object ?

Practice problem 3. An IR measurement of chemically pure carbon monoxide gas sample reported a stretch band (signal) with wavenumber of 2045 cm^-1. What is the vibration frequency of the carbon-oxygen bond in this sample?

Practice problem 4. Predict the IR wavenumber for carbon monoxide gas if all carbon atoms are of ¹³C isotope type.

Practice problem 5. Your colleague suggested that multiple stretch bands at various frequency (wavenumber) values and of possibly lower intensity could be detected for the sample described in Practice Problem 3 above. State how many stretch bands you would expect to register for this sample, explain what the reason for the multiple bands can be and predict their wavenumber values in units of cm^-1.