16.1: Spontaneity

Skills to Develop

• Distinguish between spontaneous and nonspontaneous processes
• Describe the dispersal of matter and energy that accompanies certain spontaneous processes

In this section, consider the differences between two types of changes in a system: Those that occur spontaneously and those that occur by force. In doing so, we’ll gain an understanding as to why some systems are naturally inclined to change in one direction under certain conditions and how relatively quickly or slowly that natural change proceeds. We’ll also gain insight into how the spontaneity of a process affects the distribution of energy and matter within the system.

Spontaneous and Nonspontaneous Processes

Processes have a natural tendency to occur in one direction under a given set of conditions. Water will naturally flow downhill, but uphill flow requires outside intervention such as the use of a pump. Iron exposed to the earth’s atmosphere will corrode, but rust is not converted to iron without intentional chemical treatment. A spontaneous process is one that occurs naturally under certain conditions. A nonspontaneous process, on the other hand, will not take place unless it is “driven” by the continual input of energy from an external source. A process that is spontaneous in one direction under a particular set of conditions is nonspontaneous in the reverse direction. At room temperature and typical atmospheric pressure, for example, ice will spontaneously melt, but water will not spontaneously freeze.

The spontaneity of a process is not correlated to the speed of the process. A spontaneous change may be so rapid that it is essentially instantaneous or so slow that it cannot be observed over any practical period of time. To illustrate this concept, consider the decay of radioactive isotopes, a topic more thoroughly treated in the chapter on nuclear chemistry. Radioactive decay is by definition a spontaneous process in which the nuclei of unstable isotopes emit radiation as they are converted to more stable nuclei. All the decay processes occur spontaneously, but the rates at which different isotopes decay vary widely. Technetium-99m is a popular radioisotope for medical imaging studies that undergoes relatively rapid decay and exhibits a half-life of about six hours. Uranium-238 is the most abundant isotope of uranium, and its decay occurs much more slowly, exhibiting a half-life of more than four billion years (Figure \(\PageIndex{1}\)).

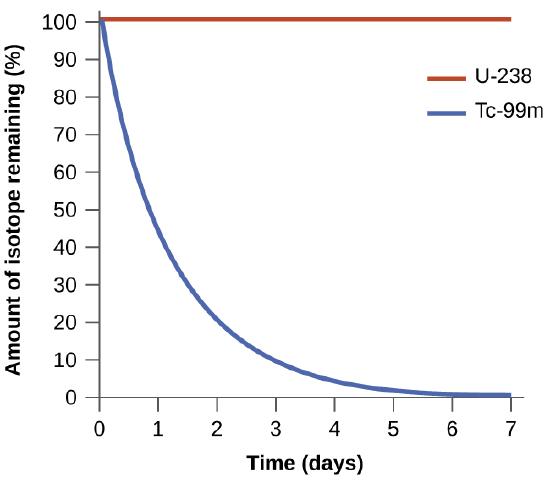
Figure \(\PageIndex{1}\): Both U-238 and Tc-99m undergo spontaneous radioactive decay, but at drastically different rates. Over the course of one week, essentially all of a Tc-99m sample and none of a U-238 sample will have decayed.

As another example, consider the conversion of diamond into graphite (Figure \(\PageIndex{2}\)).

\[\ce{C}_{(s,\textrm{ diamond})}⟶\ce{C}_{(s,\textrm{ graphite})} \label{Eq1}\]

The phase diagram for carbon indicates that graphite is the stable form of this element under ambient atmospheric pressure, while diamond is the stable allotrope at very high pressures, such as those present during its geologic formation. Thermodynamic calculations of the sort described in the last section of this chapter indicate that the conversion of diamond to graphite at ambient pressure occurs spontaneously, yet diamonds are observed to exist, and persist, under these conditions. Though the process is spontaneous under typical ambient conditions, its rate is extremely slow, and so for all practical purposes diamonds are indeed “forever.” Situations such as these emphasize the important distinction between the thermodynamic and the kinetic aspects of a process. In this particular case, diamonds are said to be thermodynamically unstable but kinetically stable under ambient conditions.

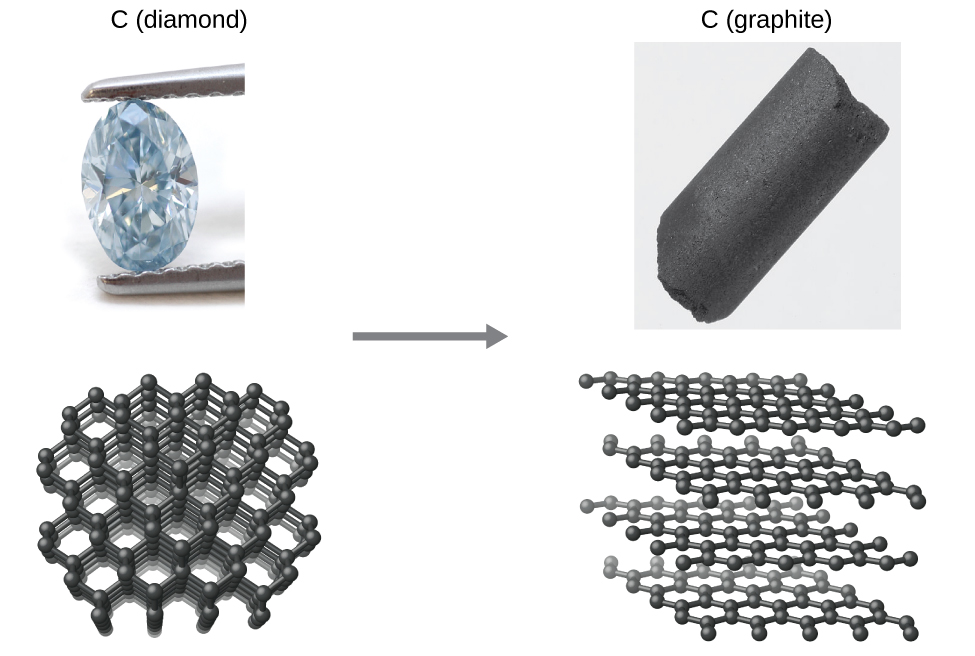
Figure \(\PageIndex{2}\):The conversion of carbon from the diamond allotrope to the graphite allotrope is spontaneous at ambient pressure, but its rate is immeasurably slow at low to moderate temperatures. This process is known as graphitization, and its rate can be increased to easily measurable values at temperatures in the 1000–2000 K range. (credit "diamond" photo: modification of work by "Fancy Diamonds"/Flickr; credit "graphite" photo: modificaton of work by images-of-elements.com/carbon.php)

Dispersal of Matter and Energy

As we extend our discussion of thermodynamic concepts toward the objective of predicting spontaneity, consider now an isolated system consisting of two flasks connected with a closed valve. Initially there is an ideal gas on the left and a vacuum on the right (Figure \(\PageIndex{3}\)). When the valve is opened, the gas spontaneously expands to fill both flasks. Recalling the definition of pressure-volume work from the chapter on thermochemistry, note that no work has been done because the pressure in a vacuum is zero.

\[w=−PΔV=0 \;\;\; \mathrm{(P=0\: in\: a\: vaccum)} \label{Eq2}\]

Note as well that since the system is isolated, no heat has been exchanged with the surroundings (q = 0). The first law of thermodynamics confirms that there has been no change in the system’s internal energy as a result of this process.

\[ΔU=q+w=0+0=0 \label{Eq3}\]

The spontaneity of this process is therefore not a consequence of any change in energy that accompanies the process. Instead, the driving force appears to be related to the greater, more uniform dispersal of matter that results when the gas is allowed to expand. Initially, the system was comprised of one flask containing matter and another flask containing nothing. After the spontaneous process took place, the matter was distributed both more widely (occupying twice its original volume) and more uniformly (present in equal amounts in each flask).

Figure \(\PageIndex{3}\):An isolated system consists of an ideal gas in one flask that is connected by a closed valve to a second flask containing a vacuum. Once the valve is opened, the gas spontaneously becomes evenly distributed between the flasks.

Now consider two objects at different temperatures: object X at temperature T_X and object Y at temperature T_Y, with T_X > T_Y (Figure \(\PageIndex{4}\)). When these objects come into contact, heat spontaneously flows from the hotter object (X) to the colder one (Y). This corresponds to a loss of thermal energy by X and a gain of thermal energy by Y.

\[q_\ce{X}<0 \hspace{20px} \ce{and} \hspace{20px} q_\ce{Y}=−q_\ce{X}>0 \label{Eq4}\]

From the perspective of this two-object system, there was no net gain or loss of thermal energy, rather the available thermal energy was redistributed among the two objects. This spontaneous process resulted in a more uniform dispersal of energy.

Figure \(\PageIndex{4}\):When two objects at different temperatures come in contact, heat spontaneously flows from the hotter to the colder object.

As illustrated by the two processes described, an important factor in determining the spontaneity of a process is the extent to which it changes the dispersal or distribution of matter and/or energy. In each case, a spontaneous process took place that resulted in a more uniform distribution of matter or energy.

Example \(\PageIndex{1}\): Redistribution of Matter during a Spontaneous Process

Describe how matter is redistributed when the following spontaneous processes take place:

1. A solid sublimes.
2. A gas condenses.
3. A drop of food coloring added to a glass of water forms a solution with uniform color.

Solution

Figure \(\PageIndex{5}\):(credit a: modification of work by Jenny Downing; credit b: modification of work by “Fuzzy Gerdes”/Flickr; credit c: modification of work by Sahar Atwa)

1. Sublimation is the conversion of a solid (relatively high density) to a gas (much lesser density). This process yields a much greater dispersal of matter, since the molecules will occupy a much greater volume after the solid-to-gas transition.
2. Condensation is the conversion of a gas (relatively low density) to a liquid (much greater density). This process yields a much lesser dispersal of matter, since the molecules will occupy a much lesser volume after the solid-to-gas transition.
3. The process in question is dilution. The food dye molecules initially occupy a much smaller volume (the drop of dye solution) than they occupy once the process is complete (in the full glass of water). The process therefore entails a greater dispersal of matter. The process may also yield a more uniform dispersal of matter, since the initial state of the system involves two regions of different dye concentrations (high in the drop, zero in the water), and the final state of the system contains a single dye concentration throughout.

Exercise \(\PageIndex{1}\)

Describe how matter and/or energy is redistributed when you empty a canister of compressed air into a room.

Answer

This is also a dilution process, analogous to example (c). It entails both a greater and more uniform dispersal of matter as the compressed air in the canister is permitted to expand into the lower-pressure air of the room.

Summary

Chemical and physical processes have a natural tendency to occur in one direction under certain conditions. A spontaneous process occurs without the need for a continual input of energy from some external source, while a nonspontaneous process requires such. Systems undergoing a spontaneous process may or may not experience a gain or loss of energy, but they will experience a change in the way matter and/or energy is distributed within the system.

Glossary

nonspontaneous process

process that requires continual input of energy from an external source

spontaneous change

process that takes place without a continuous input of energy from an external source

Contributors

• Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).