1.5: Resonance
- Page ID
- 204745
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objective
- Draw resonance forms and predict the relative contribution of each resonance form to the overall structure of the compound or ion
Recognizing resonance
Resonance contributors involve the ‘imaginary movement’ of pi-bonded electrons or of lone-pair electrons that are adjacent to (i.e. conjugated to) pi bonds. You can never shift the location of electrons in sigma bonds – if you show a sigma bond forming or breaking, you are showing a chemical reaction taking place. Likewise, the positions of atoms in the molecule cannot change between two resonance contributors.
Because benzene will appear throughout this course, it is important to recognize the stability gained through the resonance delocalization of the six pi electrons throughout the six carbon atoms. Benzene also illustrates one way to recognize resonance - when it is possible to draw two or more equivalent Lewis strucutres. If we were to draw the structure of an aromatic molecule such as 1,2-dimethylbenzene, there are two ways that we could draw the double bonds:
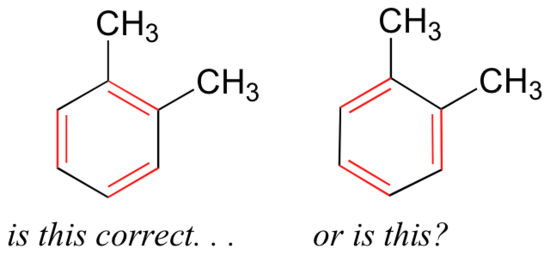
Which way is correct? There are two simple answers to this question: 'both' and 'neither one'. Both ways of drawing the molecule are equally acceptable approximations of the bonding picture for the molecule, but neither one, by itself, is an accurate picture of the delocalized pi bonds. The two alternative drawings, however, when considered together, give a much more accurate picture than either one on its own. This is because they imply, together, that the carbon-carbon bonds are not double bonds, not single bonds, but about halfway in between.
When it is possible to draw more than one valid structure for a compound or ion, we have identified resonance contributors: two or more different Lewis structures depicting the same molecule or ion that, when considered together, do a better job of approximating delocalized pi-bonding than any single structure. By convention, resonance contributors are linked by a double-headed arrow, and are sometimes enclosed by brackets:

In order to make it easier to visualize the difference between two resonance contributors, small, curved arrows are often used. Each of these arrows depicts the ‘movement’ of two pi electrons. A few chapters from now when we begin to study organic reactions - a process in which electron density shifts and covalent bonds between atoms break and form - this ‘curved arrow notation’ will become extremely important in depicting electron movement. In the drawing of resonance contributors, however, this electron ‘movement’ occurs only in our minds, as we try to visualize delocalized pi bonds. Nevertheless, use of the curved arrow notation is an essential skill that you will need to develop in drawing resonance contributors.
The depiction of benzene using the two resonance contributors A and B in the figure above does not imply that the molecule at one moment looks like structure A, then at the next moment shifts to look like structure B. Rather, at all moments, the molecule is a combination, or resonance hybrid of both A and B.
Caution! It is very important to be clear that in drawing two (or more) resonance contributors, we are not drawing two different molecules: they are simply different depictions of the exact same molecule. Furthermore, the double-headed resonance arrow does NOT mean that a chemical reaction has taken place.
Usually, derivatives of benzene (and phenyl groups, when the benzene ring is incorporated into a larger organic structure) are depicted with only one resonance contributor, and it is assumed that the reader understands that resonance hybridization is implied. This is the convention that will be used for the most part in this book. In other books or articles, you may sometimes see benzene or a phenyl group drawn with a circle inside the hexagon, either solid or dashed, as a way of drawing a resonance hybrid.

Curved arrows communicate electron flow (movement)
Curved arrows indicate electron flow. The base of the curved arrow is placed at the source of the electrons that are moving. The head of the arrow is placed at the destination of the electrons. A single barbed arrow represents one electron and a double barb represents two electrons. Electrons move from regions of relative high density to regions of low density or toward electronegative elements. It is important to use accuracy and precision when drawing curved arrows.
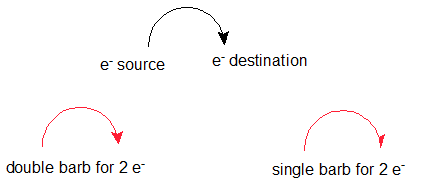
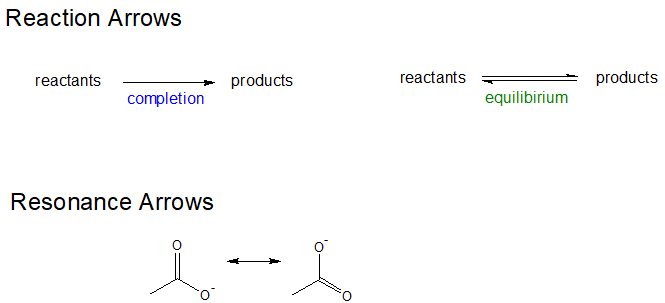
It is also important to consciously use the correct type of arrow. There are four primary types of arrows used by chemists to communicate one of the following: completion reaction, equilibrium reaction, electron movement, resonance forms. The three other types of arrows are shown below to build discernment between them.
Resonance Delocalizes Charge to Increase Stability
Resonance is most useful wen it delocalizes charge to stabilize reactive intermediates and products. Recognizing, drawing, and evaluating the relative stability of resonance contributors is essential to understanding organic reaction mechanisms.
Guidelines for drawing and working with resonance contributors
Learning to draw and interpret resonance structures, there are a few basic guidelines to help avoid drawing nonsensical structures. All of these guidellines make perfect sense as long as we remember that resonance contributors are merely a human-invented convention for depicting the delocalization of pi electrons in conjugated systems. When we see two different resonance contributors, we are not seeing a chemical reaction! We are seeing the exact same molecule or ion depicted in two different ways. All resonance contributors must be drawn as proper Lewis structures, with correct formal charges. Never show curved 'electron movement' arrows that would lead to a situation where a second-row element (ie. carbon, nitrogen, or oxygen) has more than eight electrons: this would break the 'octet rule'. Sometimes, however, we will draw resonance contributors in which a carbon atom has only six electrons (ie. a carbocation). In general, all oxygen and nitrogen atoms should have a complete octet of valence electrons.
1. There is ONLY ONE STRUCTURE for each compound or ion. This structure takes its character from the sum of all the contributors, not all resonance structures contribute equally to the sum.
2. Atoms must maintain their same position.
3. Only e- move !
4. All resonance contributors for a molecule or ion must have the same net charge.
5. Recognize which electrons can participate in resonance
a) unshared e- pairs or radicals
b) pi bond electrons
6. Recognize electron receptors
a) atoms with a positive (+) charge
b) electronegative atoms that can tolerate a negative charge
c) atoms which possess delocalizable electrons - see #4 above
7. Common electron flow patterns
a) move pi e- toward positive (+) charge or other pi bonds
b) move non-bonding e- pairs toward pi bonds
c) move single non-bonding e- toward pi bonds
Evaluating Resonance Contributors
1. Identical structures are equally important.
2. Structures will a greater number of bonds are more important.
3. Structures with charge separation are less important.
4. Pay attention to electronegativities.
5. Neutral atoms need to have complete octets.
Resonance Contributors for the Carboxylate Group
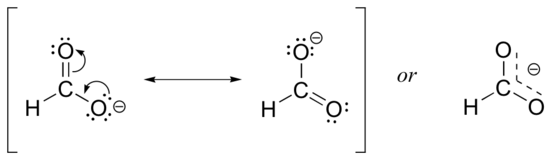
The convention of drawing two or more resonance contributors to approximate a single structure may seem a bit clumsy to you at this point, but as you gain experience you will see that the practice is actually very useful when discussing the manner in which many functional groups react. Let’s next consider the carboxylate ion (the conjugate base of a carboxylic acid). As our example, we will use formate, the simplest possible carboxylate-containing molecule. The conjugate acid of formate is formic acid, which causes the painful sting you felt if you have ever been bitten by an ant.
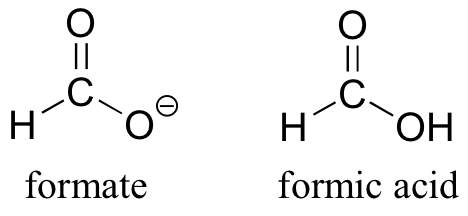
Usually, you will see carboxylate groups drawn with one carbon-oxygen double bond and one carbon-oxygen single bond, with a negative formal charge located on the single-bonded oxygen. In actuality, however, the two carbon-oxygen bonds are the same length, and although there is indeed an overall negative formal charge on the group, it is shared equally between the two oxygens. Therefore, the carboxylate can be more accurately depicted by a pair of resonance contributors. Alternatively, a single structure can be used, with a dashed line depicting the resonance-delocalized pi bond and the negative charge located in between the two oxygens.
Let’s see if we can correlate these drawing conventions to a valence bond theory picture of the bonding in a carboxylate group. We know that the carbon must be sp2-hybridized, (the bond angles are close to 120˚, and the molecule is planar), and we will treat both oxygens as being sp2-hybridized as well. Both carbon-oxygen sigma bonds, then, are formed from the overlap of carbon sp2 orbitals and oxygen sp2 orbitals.
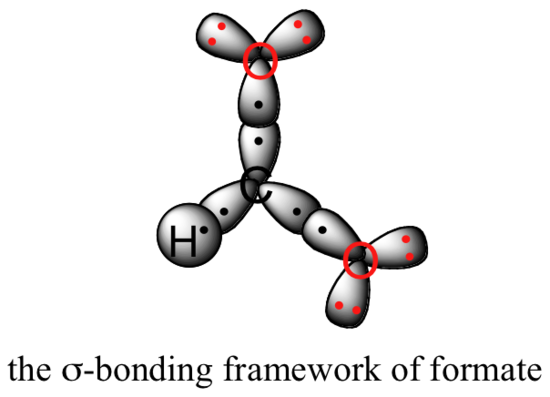
In addition, the carbon and both oxygens each have an unhybridized 2pz orbital situated perpendicular to the plane of the sigma bonds. These three 2pz orbitals are parallel to each other, and can overlap in a side-by-side fashion to form a delocalized pi bond.
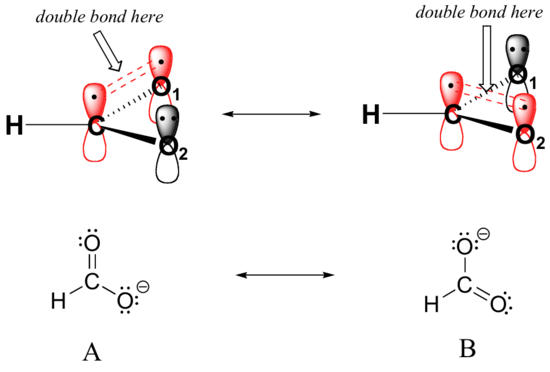
Resonance contributor A shows oxygen #1 sharing a pair of electrons with carbon in a pi bond, and oxygen #2 holding a lone pair of electrons in its 2pz orbital. Resonance contributor B, on the other hand, shows oxygen #2 participating in the pi bond with carbon, and oxygen #1 holding a lone pair in its 2pz orbital. Overall, the situation is one of three parallel, overlapping 2pz orbitals sharing four delocalized pi electrons. Because there is one more electron than there are 2pz orbitals, the system has an overall charge of –1. This is the kind of 3D picture that resonance contributors are used to approximate, and once you get some practice you should be able to quickly visualize overlapping 2pz orbitals and delocalized pi electrons whenever you see resonance structures being used. In this text, carboxylate groups will usually be drawn showing only one resonance contributor for the sake of simplicity, but you should always keep in mind that the two C-O bonds are equal, and that the negative charge is delocalized to both oxygens.
Exercise 2.13: There is a third resonance contributor for formate (which we will soon learn is considered a 'minor' contributor). Draw this resonance contributor.
Here's another example, this time with a carbocation. Recall from section 2.1 that carbocations are sp2-hybridized, with an empty 2p orbital oriented perpendicular to the plane formed by three sigma bonds. If a carbocation is adjacent to a double bond, then three 2p orbitals can overlap and share the two pi electrons - another kind of conjugated pi system in which the positive charge is shared over two carbons.

Exercise 2.14: Draw the resonance contributors that correspond to the curved, two-electron movement arrows in the resonance expressions below.
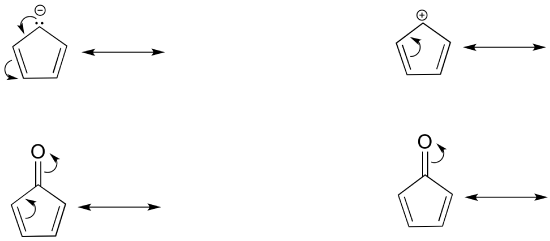
Exercise 2.15: In each resonance expression, draw curved two-electron movement arrows on the left-side contributor that shows how we get to the right-side contributor. Be sure to include formal charges.
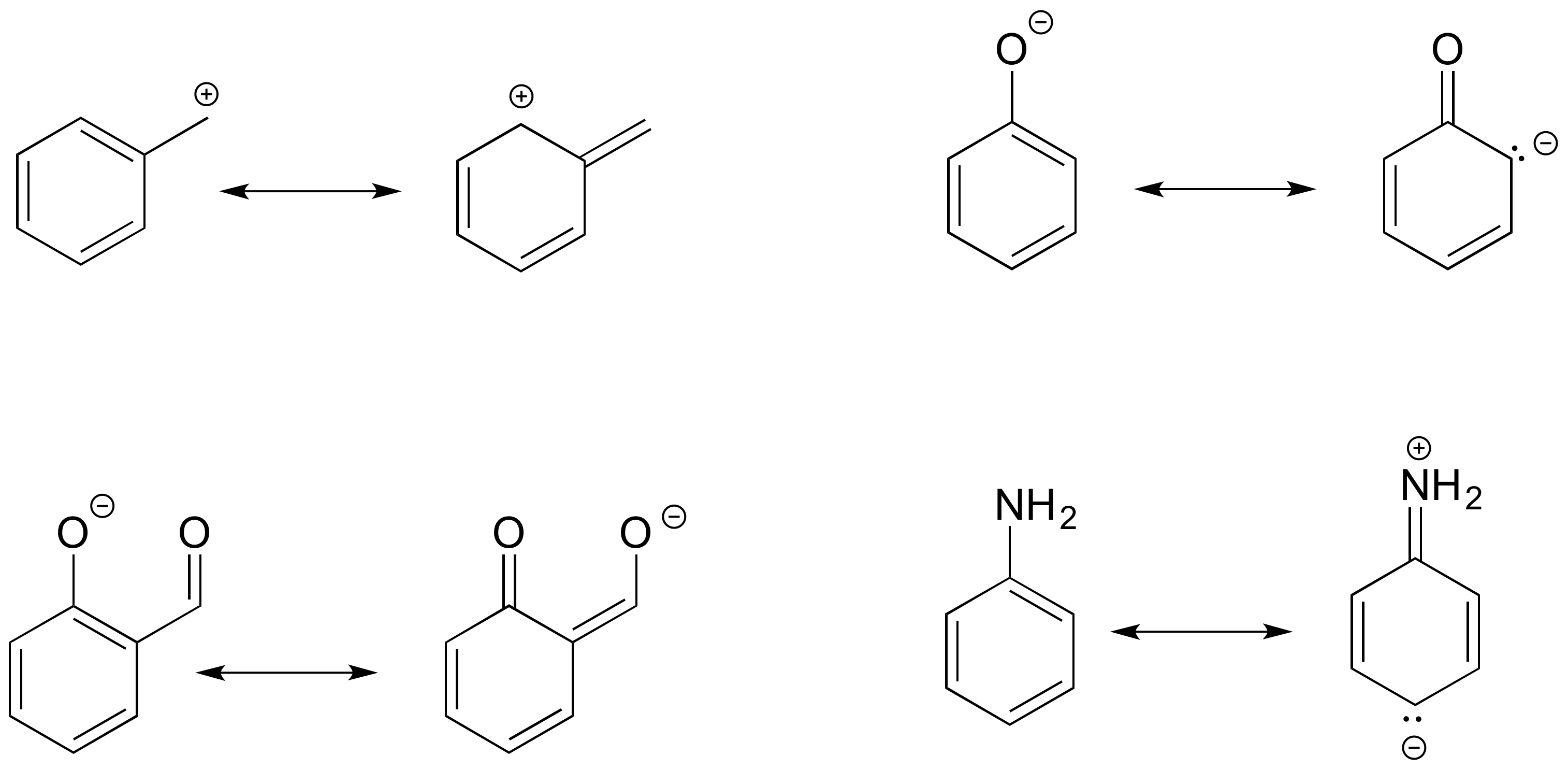
Solutions to exercises
Guided Resonance Practice
Below are a few more examples of 'legal' resonance expressions. Confirm for yourself that the octet rule is not exceeded for any atoms, and that formal charges are correct.
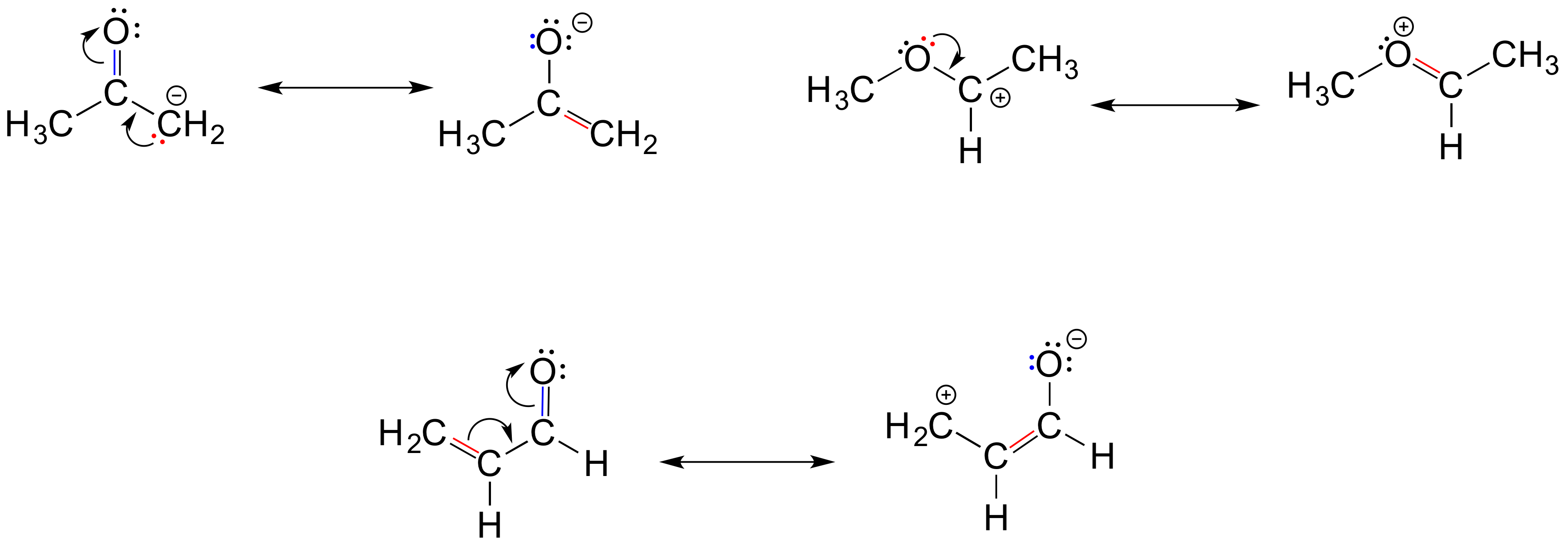
Exercise 2.16: Each of the 'illegal' resonance expressions below contains one or more mistakes. Explain what is incorrect in each.
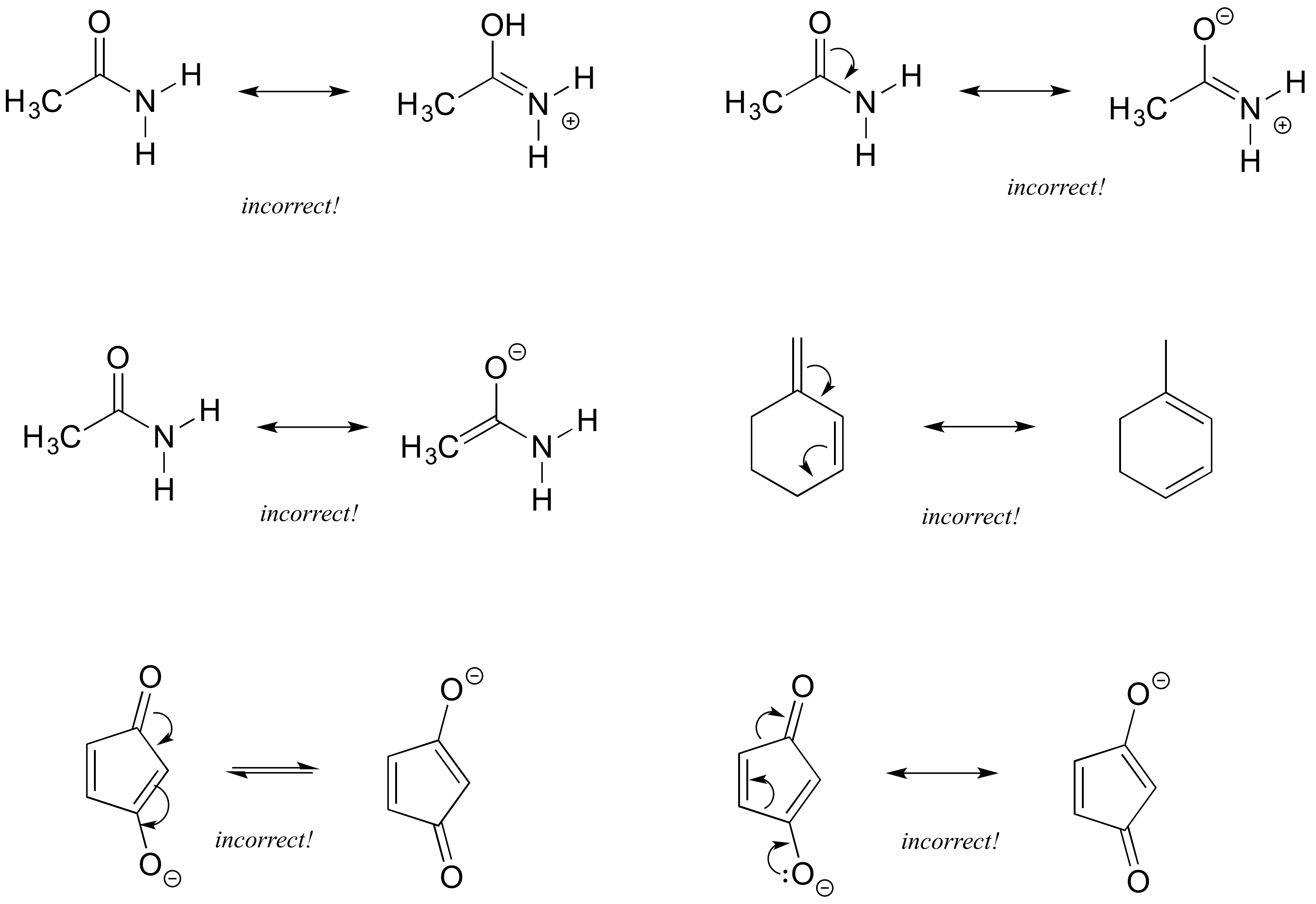
Solutions to exercises
Major vs minor resonance contributors
Different resonance contributors do not always make the same contribution to the overall structure of the hybrid - rather, in many cases one contributor comes closer to depicting the actual bonding picture than another. In the case of carboxylates, contributors A and B below are equivalent in terms of their relative contribution to the hybrid structure. However, there is also a third resonance contributor ‘C, in which the carbon bears a positive formal charge and both oxygens are single-bonded and bear negative charges.

Structure C makes a less important contribution to the overall bonding picture of the group relative to A and B. How do we know that structure C is the ‘minor’ contributor? There are four basic rules which you need to learn in order to evaluate the relative importance of different resonance contributors. We will number them 5-8 so that they may be added to in the 'rules for resonance' list earlier on this page.
Rules for determining major and minor resonance contributors:
- The carbon in contributor C does not have an octet – in general, resonance contributors in which a carbon does not fulfill the octet rule are relatively less important.
- In structure C, a separation of charge has been introduced that is not present in A or B. In general, resonance contributors in which there is a greater separation of charge are relatively less important.
- In structure C, there are only three bonds, compared to four in A and B. In general, a resonance structure with a lower number of total bonds is relatively less important.
- The resonance contributor in which a negative formal charge is located on a more electronegative atom, usually oxygen or nitrogen, is more stable than one in which the negative charge is located on a less electronegative atom such as carbon. An example is in the upper left expression in the next figure.
Below are some additional examples of major and minor resonance contributors:
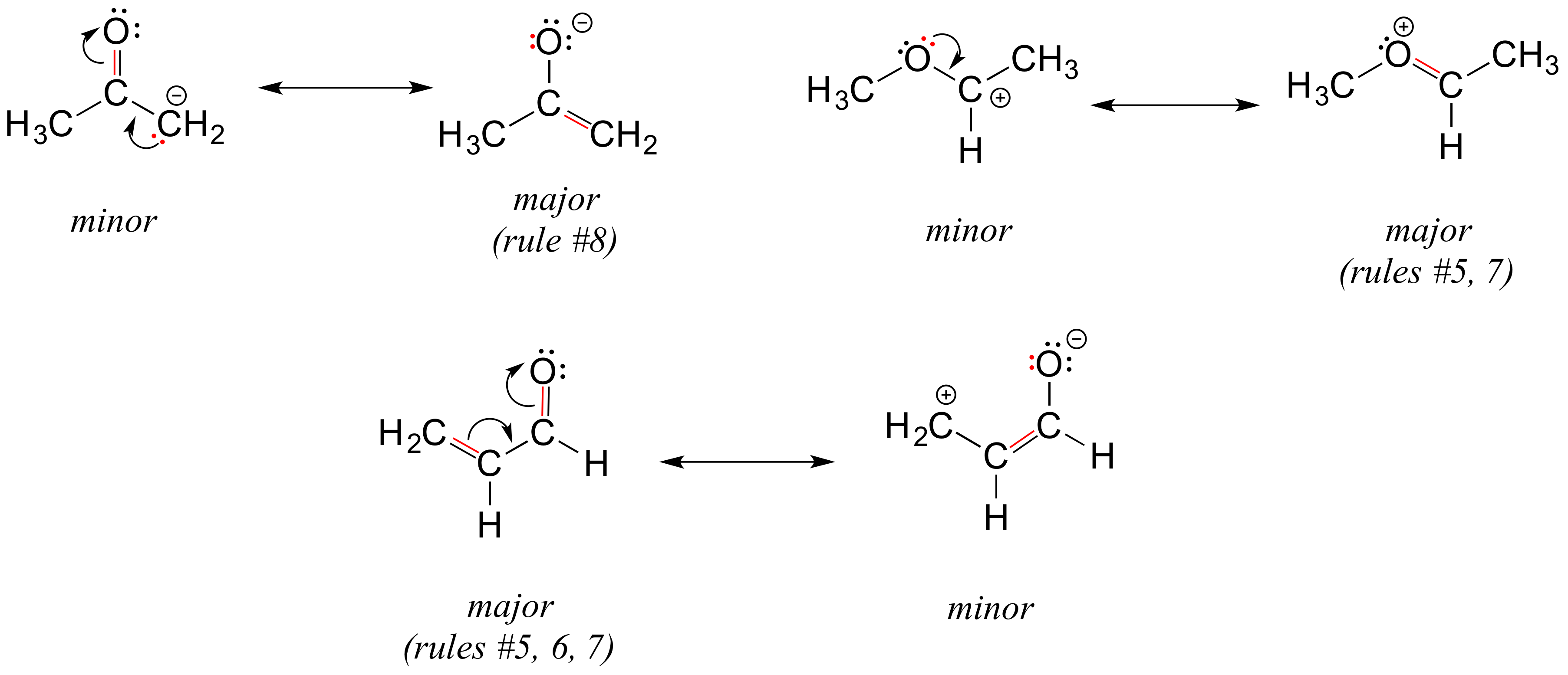
Why do we worry about a resonance contributor if it is the minor one? We will see later that very often a minor contributor can still be extremely important to our understanding of how a molecule reacts.
Exercise 2.17:
- Draw a minor resonance structure for acetone (IUPAC name 2-propanone). Explain why it is a minor contributor.
- Are acetone and 2-propanol resonance contributors of each other? Explain.
Exercise 2.18: Draw four additional resonance contributors for the molecule below. Label each one as major or minor (the structure below is of a major contributor).
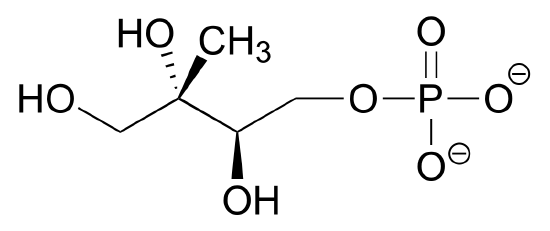
Exercise 2.19: Draw three resonance contributors of methyl acetate (IUPAC name methyl methanoate), and order them according to their relative importance to the bonding picture of the molecule. Explain your reasoning.
Solutions to exercises
Resonance and peptide bonds
What is the hybridization state of the nitrogen atom in an amide? At first glance, it would seem logical to say that it is sp3-hybridized, because, like the nitrogen in an amine, the Lewis structure shows three single bonds and a lone pair. The picture looks quite different, though, if we consider another resonance contributor in which the nitrogen has a double bond to the carbonyl carbon: in this case, we would have to say that applicable hybridization is sp2, and the bonding geometry trigonal planar rather than tetrahedral.

In fact, the latter picture is more accurate: the lone pair of electrons on an amide nitrogen are not localized in an sp3 orbital, rather, they are delocalized as part of a conjugated pi system, and the bonding geometry around the nitrogen is trigonal planar as expected for sp2 hybridization. This is a good illustration of an important point: conjugation and the corresponding delocalization of electron density is stabilizing, thus if conjugation can occur, it probably will.
One of the most important examples of amide groups in nature is the ‘peptide bond’ that links amino acids to form polypeptides and proteins.
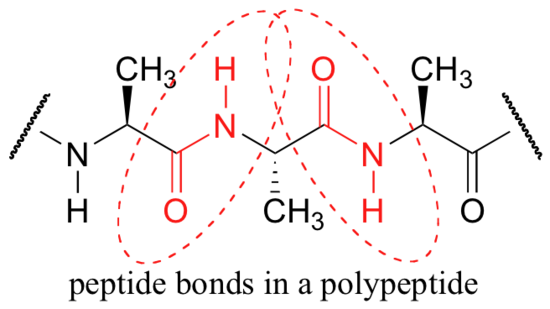
Critical to the structure of proteins is the fact that, although it is conventionally drawn as a single bond, the C-N bond in a peptide linkage has a significant barrier to rotation, indicating that to some degree, C-N pi overlap is present - in other words, there is some double bond character, and the nitrogen is sp2 hybridized with trigonal planar geometry.
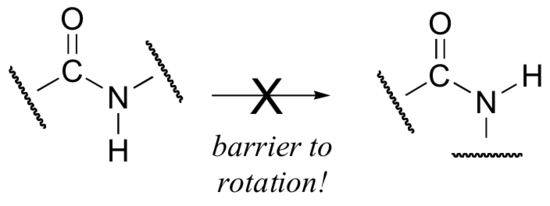
The barrier to rotation in peptide bonds is an integral part of protein structure, introducing more rigidity to the protein's backbone. If there were no barrier to rotation in a peptide bond, proteins would be much more 'floppy' and three dimensional folding would be very different.
Exercise 2.20: Draw two pictures showing the unhybridized 2p orbitals and the location of pi electrons in methyl amide. One picture should represent the major resonance contributor, the other the minor contributor. How many overlapping 2p orbitals are sharing how many pi-bonded electrons?
Exercise 2.21: Draw two pictures showing the unhybridized 2p orbitals and the location of pi electrons in the 'enolate' anion shown below. One picture should represent the major resonance contributor, the other the minor contributor. How many overlapping 2p orbitals are sharing how many pi-bonded electrons?
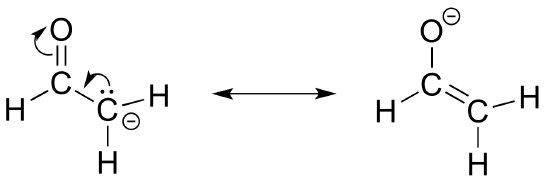
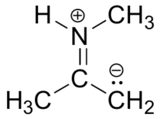
Exercise 2.22: Below is a minor resonance contributor of a species known as an 'enamine', which we will study more in chapter 12. Draw the major resonance contributor for the enamine, and explain why your contributor is the major one (refer to resonance rules #5-8 from this section).
Solutions to exercises
Solved example: Draw the major resonance contributor of the structure below. Include in your figure the appropriate curved arrows showing how you got from the given structure to your structure. Explain why your contributor is the major one. In what kind of orbitals are the two lone pairs on the oxygen?
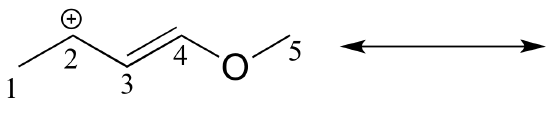
Solution: In the structure above, the carbon with the positive formal charge does not have a complete octet of valence electrons. Using the curved arrow convention, a lone pair on the oxygen can be moved to the adjacent bond to the left, and the electrons in the double bond shifted over to the left (see the rules for drawing resonance contributors to convince yourself that these are 'legal' moves).
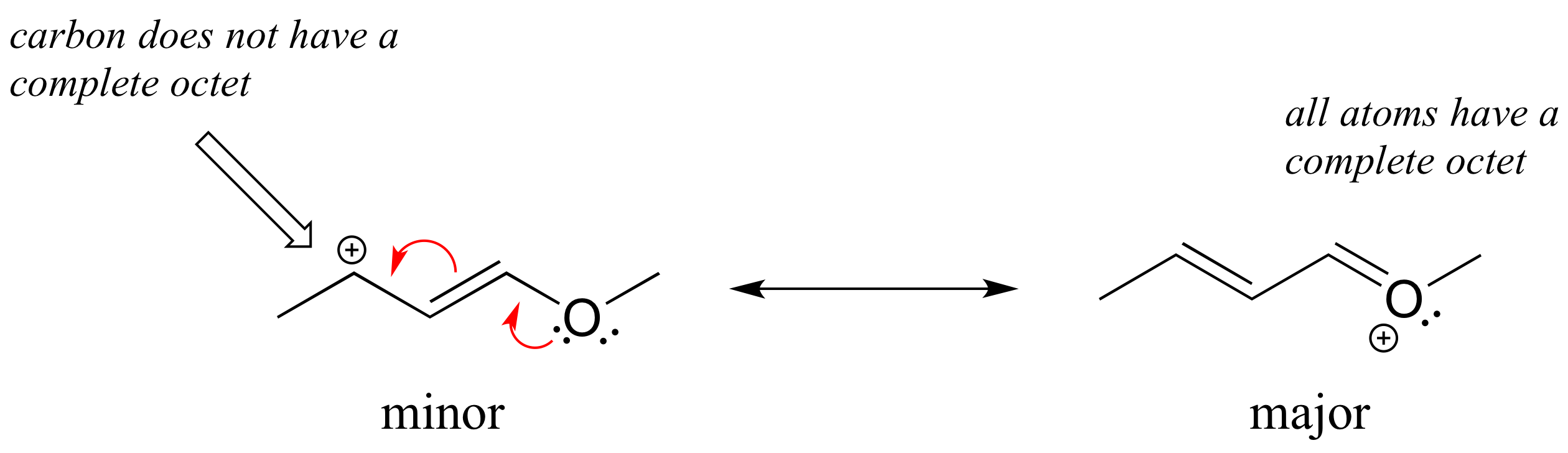
The resulting resonance contributor, in which the oxygen bears the formal charge, is the major one because all atoms have a complete octet, and there is one additional bond drawn (resonance rules #5 and #7 both apply). This system can be thought of as four parallel 2p orbitals (one each on C2, C3, and C4, plus one on oxygen) sharing four pi electrons. One lone pair on the oxygen is in an unhybridized 2p orbital and is part of the conjugated pi system, and the other is located in an sp2 orbital.
Also note that one additional contributor can be drawn, but it is also minor because it has a carbon with an incomplete octet:
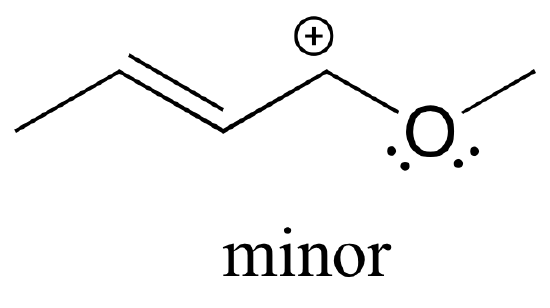
Exercise 2.23:
a) Draw three additional resonance contributors for the carbocation below. Include in your figure the appropriate curved arrows showing how one contributor is converted to the next.

b) Fill in the blanks: the conjugated pi system in this carbocation is composed of ______ 2p orbitals sharing ________ delocalized pi electrons.
Exercise 2.24: Draw the major resonance contributor for each of the anions below.
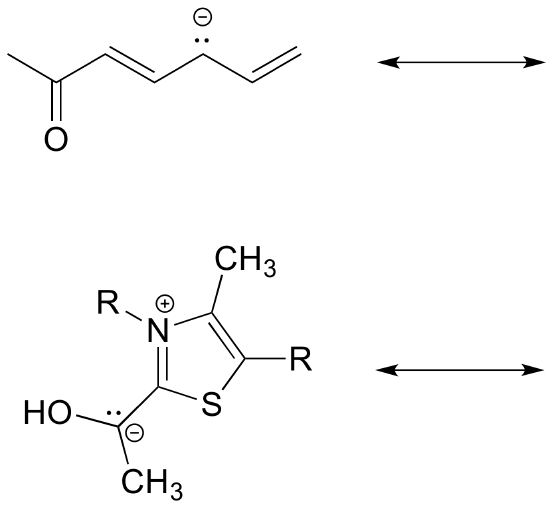
c) Fill in the blanks: the conjugated pi system in part (a) is composed of ______ 2p orbitals containing ________ delocalized pi electrons.
Exercise 2.25: The figure below shows how the negative formal charge on the oxygen can be delocalized to the carbon indicated by an arrow. More resonance contributors can be drawn in which negative charge is delocalized to three other atoms on the molecule.
a) Circle these atoms.
b) Draw the two most important resonance contributors for the molecule.
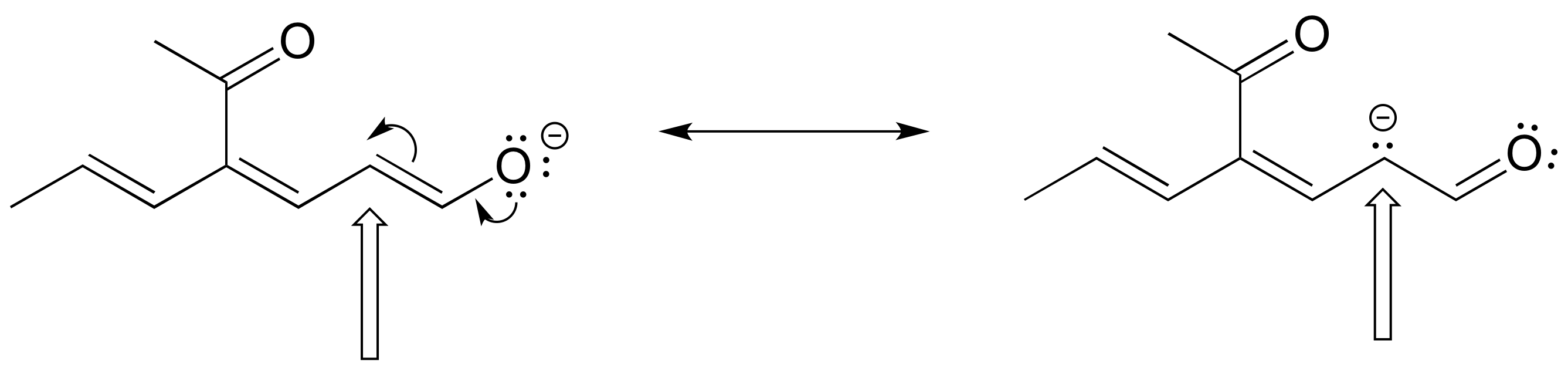
Solutions to exercises
A word of advice
Becoming adept at drawing resonance contributors, using the curved arrow notation to show how one contributor can be converted to another, and understanding the concepts of conjugation and resonance delocalization are some of the most challenging but also most important jobs that you will have as a beginning student of organic chemistry. If you work hard now to gain a firm grasp of these ideas, you will have come a long way toward understanding much of what follows in your organic chemistry course. Conversely, if you fail to come to grips with these concepts now, a lot of what you see later in the course will seem like a bunch of mysterious and incomprehensible lines, dots, and arrows, and you will be in for a rough ride, to say the least. More so than many other topics in organic chemistry, understanding bonding, conjugation, and resonance is something that most students really need to work on 'in person' with an instructor or tutor, preferably using a molecular modeling kit. Keep working problems, keep asking questions, and keep at it until it all makes sense!

