8.9: Multi-electron Considerations - A Closer Look at Helium
- Page ID
- 66729
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)If we have two identical fermions of spin \(1/2\), confined in the same region, what is the appropriate wavefunction? In the scattering case we could measure spins far from the interaction, and if we knew that the total spins is conserved, spins can be associated with each particle. In the bound state we cannot tell which particle we are measuring, so the ket must contain both spin and spatial wavefunctions of both particles.
Assuming the spins do not interact, we can separate the two-particle spin-only (ignoring the spatial part) wavefunction into \(σ(1, 2) = σ_1σ_2\). We also know the appropriate one particle basis states \(\{↑1, ↓1, ↑2, ↓2\}\), where \(↑1\) represents “particle 1” in spin up. The ONLY combinations for indistinguishable particles are then:
\[↑1↑2 \label{Trip1}\]
\[↓1↓2 \label{Trip2}\]
\[ \dfrac{1}{\sqrt{2}}(↑1↓2 + ↓1↑2) \label{Trip3}\]
\[ \dfrac{1}{\sqrt{2}} (↑1↓2 − ↓1↑2) \label{Sing1}\]
- Operating these four possible spin-only wavefunctions with \(\hat{P}_{12}\) yields the eigenvalues: 1, 1, 1 and -1 respectively.
- \(S^2 = S(S + 1)\) on yields: 2, 2, 2 and 0,
- \(S_z\) yields: 1, -1, 0 and 0.
Thus the demands of indistinguishability couples the spins of two identical particles into a triplet (\(S=1\)) and a singlet (\(S=0\)). The spin-1 vector (i.e., \(S=1\)) has three possible \(M_s\) component values (wavefunctions \(\ref{Trip1}\), \(\ref{Trip2}\), and \(\ref{Trip3}\)). This is reflected in its \(2S+1\) multiplicity and is why it is called a triplet state.
The overall wavefunction describing fermions must be antisymmetric with respect to exchange, i.e.
\[ \hat{P}_{12}|\psi \rangle = −|\psi \rangle \]
Therefore in an atom or molecule where \(Φ\) includes both spin and spatial parts, the spin and spatial parts of a fermionic wavefunction must have opposite exchange symmetry. Spin must be considered even if the energy (Coulomb potential) depends explicitly only on the spatial part. As discussed in the next section, the expectation value of the potential energy is different for symmetric and antisymmetric spatial combinations.
The Exchange Interaction
Since the overall wavefunction describing fermions must be antisymmetric with respect to exchange, i.e.
\[ \hat{P}_{12}|\psi \rangle = −|\psi \rangle ,\]
therefore in an atom or molecule where \(Φ\) includes both spin and spatial parts, the spin and spatial parts of a fermionic wavefunction must have opposite exchange symmetry. Spin must be considered even if the energy (Coulomb potential) depends explicitly only on the spatial part. However, the expectation value of the potential energy is different for symmetric and antisymmetric spatial combinations.
For helium, there asymmetric combination is
\[|Φ^{−} \rangle = \dfrac{1}{\sqrt{2}} |\phi_a(r_1)\phi_b(r_2) − \phi_a(r_2)\phi_b(r_1) \rangle \label{ASym}\]
and symmetric combination is
\[ |Φ^{+} \rangle = C_{ab} |\phi_a(r_1)\phi_b(r_2) + \phi_a(r_2)\phi_b(r_1) \rangle + C_{aa} |\phi_a(r_2)\phi_a(r_1) \rangle + C_{bb}|\phi_b(r_2)\phi_b(r_1) \rangle \label{Sym}\]
For convenience, let's consider only the \(|Φ^{\pm} \rangle\) combinations with \(C_{aa} = C_{bb}=1\)). The corresponding energy associated with the inter-electron interaction potential \(V\) can be expanded
\[ \langle \psi ^{\pm} |\hat{V} |\psi ^{\mp} \rangle = \langle \phi_a(r_1)\phi_b(r_2)|V(r)|\phi_a(r_1)\phi_b(r_2)\rangle \pm \langle \phi_a(r_1)\phi_b(r_2)|V(r)|\phi_a(r_2)\phi_b(r_1) \rangle \]
The first term is called the Coulomb interaction (\(J\)) and the second term is known as the exchange interaction (\(K\)): a measurable contribution to the energy comparable in size to the first, which has no classical analog.
Now notice something strange. The exchange interaction has split the \(S=1\) states from the \(S=0\) states. We could write the potential as
\[\hat{V} = J_{nl} − (2\hat{S} − 1)K_{nl}\]
even though the Hamiltonian does not act on the spin! This is because the sign of the exchange integral depends on the (anti)symmetry of the spatial wavefunction. Thus we can write the matrix element as
\[ \langle \psi |J_{nl} − (2S − 1)K_{nl}| \psi \rangle \]
This ‘exchange interaction’ depends on the spin; the triplet states have lower energy than the singlet (this is one of Hund’s rules for determining energy levels in atoms).
Helium
Helium is the simplest system for which we are unable to accurately calculate the energy. For a single electron moving in the field of a helium nucleus, the spatial wavefunctions are similar to those of hydrogen \(|\phi_{n,l,m_s} \rangle\). When a second electron is added, a reasonable basis set is exchange-symmetrized wavefunctions consisting of spin states multiplying hydrogenic spatial parts:
\[(\phi _{n,l,m}(r_1) \phi _{n',l' ,m_l'}(r_2) ± \phi _{n,l,m}(r_2) \phi _{n',l' ,m_l'}(r_1))\]
The overall wavefunction must be antisymmetric so:
- the singlet spin states (exchange-antisymmetric) must combine with symmetric spatial states and
- the triplet spin states (exchange-symmetric) must combine with antisymmetric spatial states.
If both electrons were in the same spatial state (orbital), the antisymmetric spatial wavefunction would be:
\[|(a(r_1)a(r_2) − a(r_2)a(r-1))\rangle = 0\]
Hence, there is no triplet for the ground state.
Electron-electron interaction - ground state by perturbation theory
The hydrogen wavefunctions are only a choice of basis set: the hydrogenic potential ignores the electron-electron repulsion. A simple approach is to treat this as a perturbation and to use degenerate perturbation theory. The perturbation potential is just
\[V = \dfrac{e^2}{4π \epsilon_0 r_{12} }\]
where \(r_{12} = |r_1 − r_2|\). For helium, the unperturbed spatial ground state is just a product of the \(1s\) hydrogenic ones with \(Z=2\) :
\[ \phi _{n=1,l=0,m_l=0} (r_1) \phi _{n=1,l=0,m_l=0} (r_2) = \dfrac{ Z^3}{πa^3_0} \exp[−Zr_1/a_0] \exp [−Zr_2/a_0]\]
The zero-order energy (i.e., unperturbed energy) associated with this wavefunction is
\[ E^{0}=\dfrac{4Z e^4}{\hbar^2} \label{Zero}\]
Via first-order perturbation theory, the energy shift from the perturbed energy of any state is
\[\langle \phi | \dfrac{e^2}{4π \epsilon_0 r_{12} }| \phi \rangle \label{General}\]
and for the ground state fo Helium, Equation \(\ref{General}\) is given by:
\[\langle \phi _{n=1,l=0,m_l=0} (r_1) \phi _{n=1,l=0,m_l=0} (r_2)| \ \dfrac{e^2}{4π \epsilon_0 r_{12} }| \phi _{n=1,l=0,m_l=0} (r_1) \phi _{n=1,l=0,m_l=0} (r_2) \rangle \label{First}\]
Comparison of the zero-order energy and the measured energy show that electron-electron repulsion is over 30% of the unperturbed energy (Equation \(\ref{Zero}\)), so perturbation theory may seem inappropriate (although higher order perturbation theory may be used). Strictly, Equation \(\ref{First}\) is not even the right integral, as it neglects electron correlation effects (discussed elsewhere), but the value of this integral
\[\dfrac{5Z e^4}{8 \hbar ^2}\]
is within 5% of the actual energy.
Note also that the radial wavefunctions are different for \(2s\) and \(2p\), so the electron-electron interaction splits the degeneracy between \(1s2s\) and \(1s2p\) configurations.
Multiplicity and Degeneracy of Excited States
Ignoring electron-electron interaction (e.g., in the hydrogen atom), all \(1s2s\) and \(1s2p\) states have the same energy. However, the electron-electron perturbation
\[ H^{1} = \dfrac{e^2}{4π \epsilon_0 r_{12}}\]
lifts that degeneracy, which we can treat with degenerate perturbation theory (this is outside the scope of this class). Rather than evaluating resulting perturbation theory integral exactly, we can use a physical argument about the nature of the perturbation. Since (\(e^2/4π \epsilon_0 r_{12}\)) is not an externally applied potential, it applies no net torque nor force on the electrons. The perturbation cannot change the angular momentum, so it cannot mix states with different \(l\) or \(m_l\) (i.e., the perturbed wavefunctions does not have components of differing angular momentum quantum numbers). Integrating over \(\theta\) results in \(δ_{ll'}\) and integrating over \(\phi\) give \(δ_{m_lm_l'}\), so total orbital angular momentum remains a good quantum number, hence:
\[\begin{align*} L &= \sum_{i=1}^2 l_i \\[4pt] &= 0 + 0 \\[4pt] &= 0 \end{align*}\]
for the \(1s^12s^1\) electron configuration (promoting a 1s electron to the 2s orbital) or
\[\begin{align*} L &= \sum_{i=1}^2 l_i \\[4pt] &= 0 + 1 \\[4pt] &= 1 \end{align*}\]
for the \(1s^12p^1\) electron configuration (promoting a 1s electron to the 2p orbital).
Different electron configurations will have different total orbital angular momentum and spin angular momentum amplitudes.
Since the 2s electron is less well screened from the nuclear charge by the \(1s\) that the \(2p\) electron due to its closer radial distribution function, it will have lower energy (see Slater's Rules). As wth the helium ground-state, for a given spatial excited state, the possible normalized spin-orbital wavefunction combinations, consistent with the antisymmetry requirement are a triplet (\(S=1\)) and a singlet (\(S=0\)).
The spin-orbital wavefunctions for the triplet state are
\[\Phi _3 = \dfrac{1}{\sqrt{2}} [ \phi_{n,l,m_l, n',l',m_l'} - \phi_{n',l',m_l', n,l,m_l} ] (↑ ↑ )\]
and
\[ \dfrac{1}{\sqrt{2}} [ \phi_{n,l,m_l, n',l',m_l'} - \phi_{n',l',m_l', n,l,m_l} ] (↓↓)\]
and
\[ \dfrac{1}{2} [ \phi_{n,l,m_l, n',l',m_l'} - \phi_{n',l',m_l', n,l,m_l} ] (↓↑ + ↓↑)\]
The spin-orbital wavefunction for the singlet state is
\[ \Phi _1 = \dfrac{1}{2} [ \phi_{n,l,m_l, n',l',m_l'} + \phi_{n',l',m_l', n,l,m_l} ] (↓↑ - ↓↑) \label{SingWave}\]
where \(\phi_{n,l,m_l, n',l',m_l'} \rangle\) represents electron 1 in a hydrogenic state with quantum numbers \(n\), \(l\) and \(m_l\) and electron 2 with \(n'\), \(l'\), and \(m_l\). The subscripts on the \(\Phi\) label spin multiplicity
\[2S+1\]
Again, whole effect of the potential is contained in the spatial part, the spin integral will be \(\delta _{\sigma, \sigma'}\). So off-diagonal matrix elements are all zero. We need to evaluate two types of integrals to compute the energies of these states:
- the Coulomb integral
\[J_{nl} = \langle \phi_{n,l,m_l, n',l',m_l'} | \dfrac{e^2}{4π \epsilon_0 r_{12}} | \phi_{n,l,m_l, n',l',m_l'} \rangle \]
- and the Exchange integral
\[K_{nl} = \langle \phi_{n,l,m_l, n',l',m_l'} | \dfrac{e^2}{4π \epsilon_0 r_{12}} | \phi_{n',l',m_l', n,l,m_l} \rangle \]
Within first-order perturbation theory, an energy shift can be calculated by Equation \(\ref{General}\). Apply this expression to the \(1s^12s^1\) singlet state wavefunction (Equation \(\ref{SingWave}\)) results in:
\[ E^1 = \dfrac{1}{2} \dfrac{e^2}{4 \pi \epsilon_o} \left( \langle\phi_{100,200} | \dfrac{1}{r_{12}}| \phi_{100,200}\rangle + \langle \phi_{200,100} | \dfrac{1}{r_{12}}| \phi_{200,100}\rangle \pm \langle\phi_{100,200} | \dfrac{1}{r_{12}}| \phi_{200,100}\rangle \pm \langle \phi_{200,100} | \dfrac{1}{r_{12}}| \phi_{100,200} \rangle \right)\]
which in terms of the integrals defined above can be rewritten
\[ E^1 = \dfrac{1}{2} \left( J_{1,2} + J_{2,1} \pm K_{1,2} \pm K_{2,1} \right) \]
since \(J_{1,2} = J_{2,1}\) and \(K_{1,2} = k_{2,1}\), then
\[ E^1 = J \pm K\]
where the + applies to the singlet state (the 1s and 2s electrons have opposing spin) and the − to the triplet (the electrons aligned). The Coulomb integral as a measure of the electron-electron repulsion, increases the energy of the state. However, the exchange integral can either increase (for singlets) or decrease energy (for triplets). This means that electron-electron repulsion lifts the degeneracy two-fold:
- the energy levels are split by different direct interactions into \(L=0\) and \(L=1\) and
- the energy levles are again split through exchange interaction into singlet and triplet.
The final degeneracies of states of helium with one electron excited to \(n=2\) are 3, 1, 9 and 3 (Figure \(\PageIndex{1}\)).
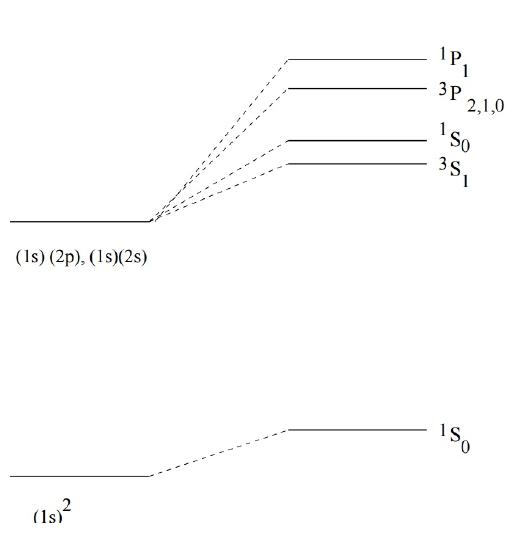
The spectroscopic notation in Figure \(\PageIndex{1}\) is called a term symbol and expresses the quantum numbers as:
\[^{2S+1}L_J \]
where \(J\) is the total angular moment.
The ‘exchange force’ selects preferred spin state via the requirement of overall antisymmetry of the wavefunction.
Contributors and Attributions
Graeme Ackland (University of Edinburgh)

