Lecture Extra III: Coupling Angular Momenta and Atomic Term Symbols
- Page ID
- 40114
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Last lecture address two unique aspects of electrons: spin and indistinguishability and how they couple into describing multi-electron wavefunctions. The spin results in an angular momentum that follows the same properties of orbital angular moment including commutators and uncertainty effect. The Slater determinant wavefunction was introduced as a way to consistently address both properties.
Remember that the Electronic Configuration is not enough to describe the wavefunction of a multi-Electron Atom
Specification of a particular occupancy of the set of orbitals available to the system gives an electronic configuration. For example,
- \(1s^22s^22p^2\) is an electronic configuration for the carbon atom (and the \(N^{+1}\) and the \(O^{-2} \) ions)
This configuration represent situations in which the electrons occupy low-energy orbitals of the system and, as such, are likely to contribute strongly to the true ground and low-lying excited states and to the low-energy states of molecules formed from these atoms or ions.
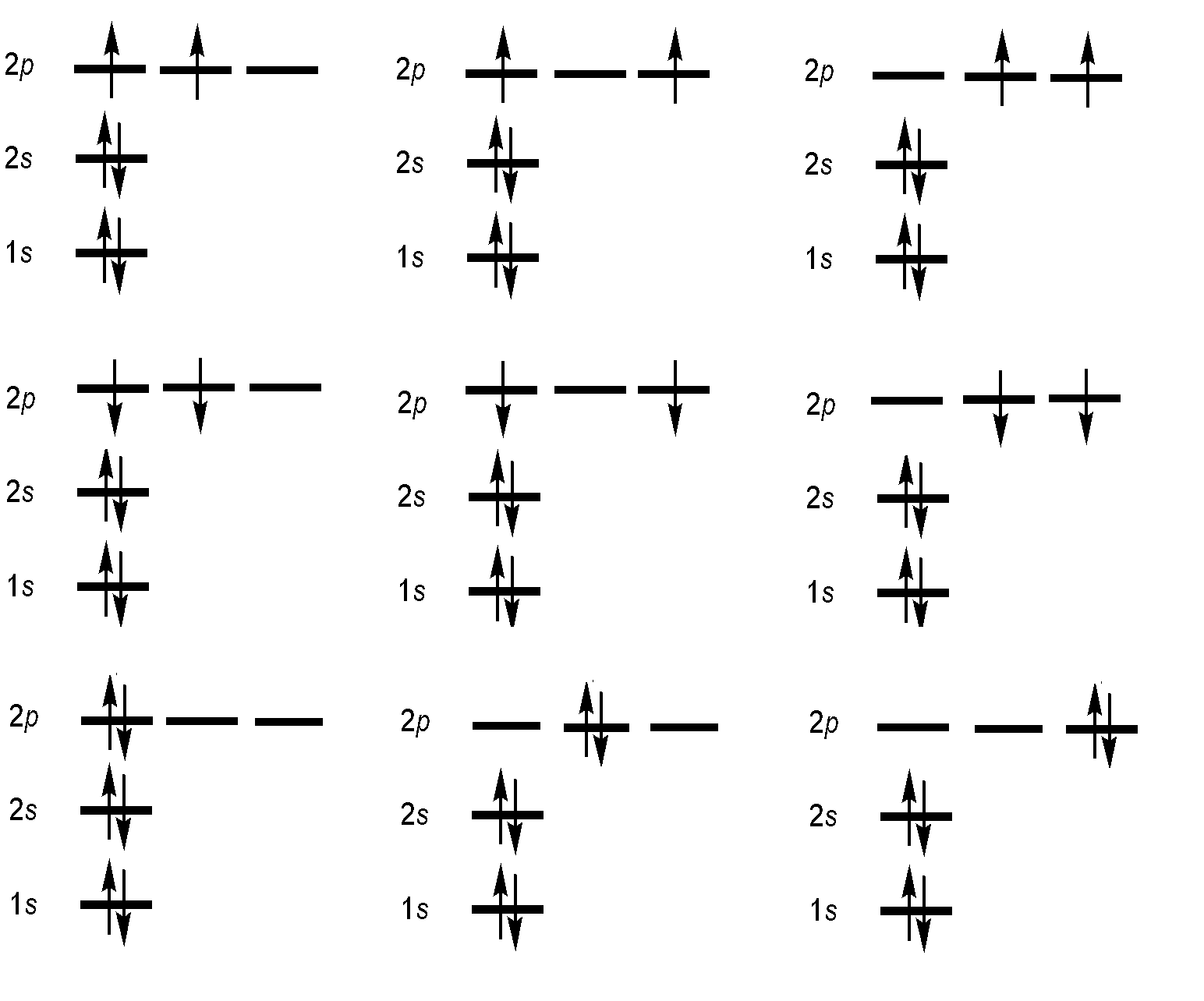
Specification of an electronic configuration does not, however, specify a particular electronic state of the system. For the electronic configuration of carbon with \(1s^22s^22p^2\), there are many ways in which the 2p orbitals can be occupied by the two electrons. As a result, there are a total of multiple "microstates" which cluster into energetically distinct levels, lying within this single configuration.
Specifying the orbital configuration of an atom does not uniquely identify the electronic state!
We want to Couple Angular Momenta to Describe Microstates
Specifying the orbital configuration of an atom does not uniquely identify the electronic state of the atom because the orbital angular momentum, the spin angular momentum, and the total angular momentum are not precisely specified. For example in the 2p electron in Boron can be in any of the three p-orbitals, \(m_l\) = +1, 0, and –1, and have spins with \(m_s\) = +1/2 or –1/2. Thus, there are 3 times 2 different possibilities spin-orbitals this electron can "be in".
Specifying the orbital configuration of an atom does not uniquely identify the electronic state!
The orbital and spin angular momentum of the electrons combine in multiple ways to produce angular momentum vectors that are characteristic of the entire atom not just individual electrons, and these different combinations can have different energies. There are two descriptions for the coupling of angular momentum. One is called j-j coupling, and the other is called L-S coupling. The j-j coupling scheme is used for heavy elements (z > 40), and the L-S coupling scheme is used for the lighter elements.

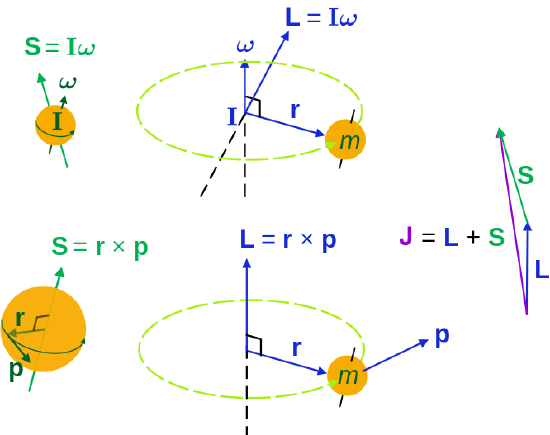
Classical picture of an orbiting spinning electron. The electron has both orbital and spin angular momenta.
L-S coupling: The Single Classical Rotating and Revolving Electron Case
We have introduced to types of angular momenta in class so far:
- Orbital angular momenta (\(l\)) is the quantum-mechanical counterpart to the classical notion of angular momentum: it arises when a particle executes a rotating or twisting trajectory (such as when an electron orbits a nucleus)
- Spin angular momenta (\(s\)) is an intrinsic form of angular momentum carried by elementary particles. The existence of spin angular momentum is inferred from experiments, such as the Stern–Gerlach experiment.
These two angular momenta are vectors to "adding" them requires vector addition. That means you cannot simple add magnitudes of the momenta but need to know the direction of the momenta.
Let's introduce a new "momentum" call the total angular momentum.
- Total angular momentum (\(J\)) combines both the spin and orbital angular momentum of all particles and fields.
Both types of momenta are vector quantities with a definite magnitude and orientation. Classically the three types of spin are demonstrated below.
from Wikipedia (public domain)
Angular momenta of a classical object.
- Left: "spin" angular momentum S is really orbital angular momentum of the object at every point,
- right: extrinsic orbital angular momentum L about an axis,
- top: the moment of inertia tensor I and angular velocity ω (L is not always parallel to ω),
- bottom: momentum p and its radial position r from the axis.The total angular momentum (spin plus orbital) is J. For a quantum particle the interpretations are different; particle spin does not have the above interpretation.
For a single particle the three momenta are simply expressed
\[\vec{J} = \vec{L} + \vec{S}\]
Conservation of angular momentum applies to J, but not to L or S. Hence, angular momentum to transfer back and forth between L and S, with the total (J) remaining constant.
We can understand this qualitatively in the vector model pictured below. We are adding two quantum vectors.

The length of the resulting vector is somewhere between the difference of their magnitudes and the sum of their magnitudes, since we don't know which direction the vectors are pointing.
The Single Quantum Rotating and Revolving Electron Case (with Quantization and Uncertainty)
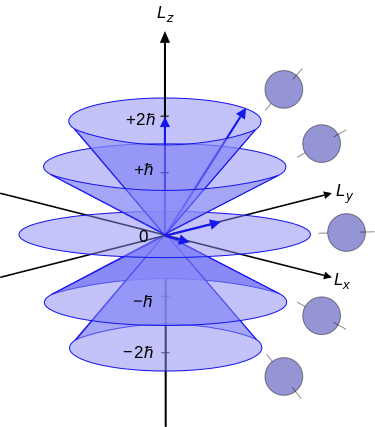
Remember the discussion about angular momentum before: we can know the magnitude or specifically the square of the magnitude (\(L^2\)) and project of angular momentum in one direction, typically the z-direction \(L_z\), but cannot know the other two. This quantum uncertainty was mathematically was represented by the cyclic permutations:
\[[L_x, L_y] = {\rm i}\,\hbar\, L_z \]
\[[L_y, L_z] = {\rm i}\,\hbar\, L_x \]
\[[L_z, L_x] = {\rm i}\,\hbar\, L_y \]
and
\[[L^2, L_z] = 0\]
These suggest the continuum of all possible angular momenta for a corresponding specified quantum number:
- One direction is constant (z-axis), the other two are variable.
- The magnitude of the vectors must be constant (for a specified state corresponding to the quantum number), so the two indeterminate components of each of the vectors must be confined to a circle, in such a way that the measurable and un-measurable components (at an instant of time) allow the magnitudes to be constructed correctly, for all possible indeterminate components.
The same types of cyclic permutations exist for spin
\[[S_x, S_y] = {\rm i}\,\hbar\, S_z \]
\[[S_y, S_z] = {\rm i}\,\hbar\, S_x \]
\[[S_z, S_x] = {\rm i}\,\hbar\, S_y \]
and
\[[S^2, S_z] = 0\]
And also expressed in uncertainty cones
.
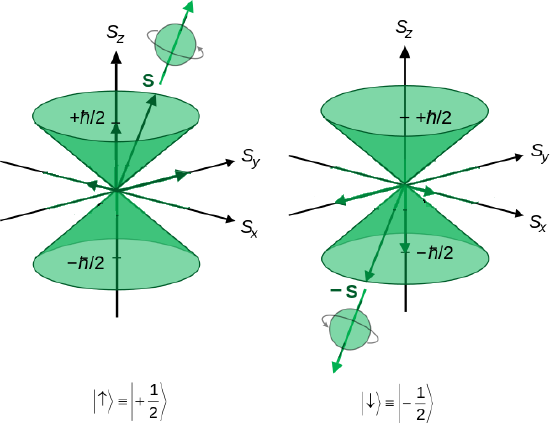
(left) Illustration of the vector model of orbital angular momentum.A set of states with quantum numbers \(l=2\), and \(m_l= = -2, -1, 0, +1, +2\). from Wikipedia (Public Domain) (right) Heuristic depiction of spin angular momentum cones for a spin-1/2 particle. (Public Domain; Maschen).
For orbital angular momenta the eigenvalues for \(L^2\) and \(L_z\) are quantified (naturally)
\[ L^2 \,| = l\,(l+1)\,\hbar^2\,Y_{l\,m}\]
where \(l\) is an integer. The eigenvalue for spin angular momenta (of an electron) the \(s\) quantum number is only either +1/2 or -1/2
\[ S^2 \,| spin \rangle = s\,(s+1)\,\hbar^2\, | spin \rangle \]
The same types of permutations exist for total angular momenta
\[[J_x, J_y] = {\rm i}\,\hbar\, J_z \]
\[[J_y, J_z] = {\rm i}\,\hbar\, J_x \]
\[[J_z, J_x] = {\rm i}\,\hbar\, J_y \]
and
\[[J^2, J_z] = 0\]
The magnitudes satisfy all of the following, in terms of operators and vector components:
\[\begin{align}& \hat{L}^2 = \hat{L}_x^2 + \hat{L}_y^2 +\hat{L}_z^2 \,\, \rightleftharpoons \,\, \bf{L}\cdot\bf{L}= L^2 = L_x^2 + L_y^2 + L_z^2,\\& \hat{S}^2 = \hat{S}_x^2 + \hat{S}_y^2 +\hat{S}_z^2 \,\, \rightleftharpoons \,\, \bf{S}\cdot\bf{S}= S^2 = S_x^2 + S_y^2 + S_z^2,\\& \hat{J}^2 = \hat{J}_x^2 + \hat{J}_y^2 +\hat{J}_z^2 \,\, \rightleftharpoons \,\, \bf{J}\cdot\bf{J}= J^2 = J_x^2 + J_y^2 + J_z^2,\\\end{align} \]
and quantum numbers:
\[ |\bf{L}| = \hbar \sqrt{\ell(\ell+1)}, \quad L_z = m_\ell \hbar \]
\[ |\bf{S}| = \hbar \sqrt{s(s+1)}, \quad S_z = m_s \hbar\]
\[|\bf{J}| = \hbar \sqrt{j(j+1)}, \quad J_z = m_j \hbar\]
where
- \(l\), is the azimuthal quantum number,
- \(s\), is the spin quantum number intrinsic to the type of particle,
- \(j\), is the total angular momentum quantum number,
The Multiple Quantum Rotating and Revolving Electron Case (with Quantization and Uncertainty)
The angular momentum of \(N\) particles is the vector sum of constituent particles
\[ \vec{L} = \sum_i^N \vec{l}_i\]
and the z-component of is the scalar sum
\[ L_z = \sum_i^N L_{z,i}\]
The spin momentum of \(N\) particles is the vector sum of constituent particles
\[ \vec{S} = \sum_i^N \vec{s}_i\]
and the z-component of is the scalar sum
\[ S_z = \sum_i^N S_{z,i}\]
The total spin momentum of \(N\) particles is the vector sum of constituent particles
\[ \vec{J} = \sum_i^N \vec{J}_i\]
and the z-component of is the scalar sum
\[ J_z = \sum_i^N J_{z,i}\]
The process of adding all angular momenta together is a laborious task, since the resultant momenta is not definite, the entire cones of precessing momenta about the z-axis must be incorporated into the calculation. This can be simplified by some developed approximations - such as the Russell-Saunders coupling scheme in L-S coupling, named after H. N. Russell and F. A. Saunders (1925).

Illustration of L-S coupling. Total angular momentum J is purple, orbital L is blue, and spin S is green.
Or without cones
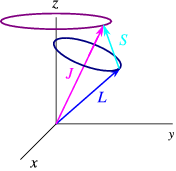
http://oer.physics.manchester.ac.uk/
Permitted values of J again, given by a Clebsch-Gordon series
\[\large \color{red} J = L + S, L + S - 1, L + S - 2 .... |L - S |\]
This is because this equation discussed magnitude of the total angular momentum, which is a results of vector addition and since there are different orientations of L and S, the magnitude of their vector sum will depends on the orientation (not just the lengths).
Angular Momentum (Spin and Orbital) Multiplicity
Quantum mechanics states that the component of angular momentum measured along any direction can only take on the values
\[ L_z = \hbar m_l\]
with
\[m_l \in \{ - l, -(l-1), \dots, l - 1, s \} \]
where \(L_z\) is the spin component along the z-axis, \(m_l\) is the spin projection quantum number along the z-axis. One can see that there are \(2L+1\) possible values of \(L_z\). The number "2L + 1" is the multiplicity of the spin system (referred to this as degeneracy before).
So the multiplicity of state with orbital angular momenta \(L\)
\[2L+1\]
and for spin angular momenta \(S\)
\[2S+1\]
Notice that these equations involve BIG \(L\) for all electrons in the atom, not \(ell\) for one electron. The same for sping.
Number of Microstates
The number of microstates (given \(S\) and \(L\)) is given by:
\[\dfrac{G!}{N!(G−N)!}\]
where \(G\) is the number of spin orbitals and \(N\ is the number of electrons.
If \(N = G\), then the number of states is 1.
The number of states per term symbol can also be found:
\[\underbrace{(2L + 1)}_{\text{orbital multiplicity}} \times \overbrace{(2S + 1)}^{\text{spin multiplicity}}\]
How many possible states are there for a single spin-1/2 particle (e.g. electron) with \(m_s = +1/2\) and \(m_s = −1/2\).)?
- Answer
-
The spin multiplicity of a single electron is
\[2S+1 = 2 (1/2) +1 =2 \]
These correspond to quantum states in which the spin is pointing in the +z or −z directions respectively, and are often referred to as "spin up" and "spin down".
Compare this for a spin-3/2 particle (which exist), the multiplicity is \(2S+1 = 2 (3/2) +1 = 4\). So the possible values of \(m_s\) are +3/2, +1/2, −1/2, −3/2. This is important for NMR spectroscopy, by the way.
There are only two possible values for a spin-1/2 particle like the electron. This is not surpising.
What about a a two-electron system?
- Answer
-
For a two electron system each electron can occupy two states (four total), but due to indistinguishability, these are are really two states
½ and ½ (aligned spins)
½ and - ½ (opposed spins)
which correspond to
\( S = ½ + ½ = 1\) and \(S= ½ - ½ = 0\)
The multiplicity of these two states (\(2S+1\)) are then
For \(S =1\):
\[2S+1 = 3\]
This is called a triplet state since there are actually three states (commonly called microstates) that represent this state
For \(S=0\):
\[2S+1 = 1 \]
This is called a singlet state since only one state represents it.
It should be noted that for multi-electron systems where all electrons are paired, the system is in a singlet. Also note that singlets are diamagnetic, while triplets are paramagnetic.
You probably learned about paramagnetism and diamagnatism in general chemistry, specifically crystal field theory
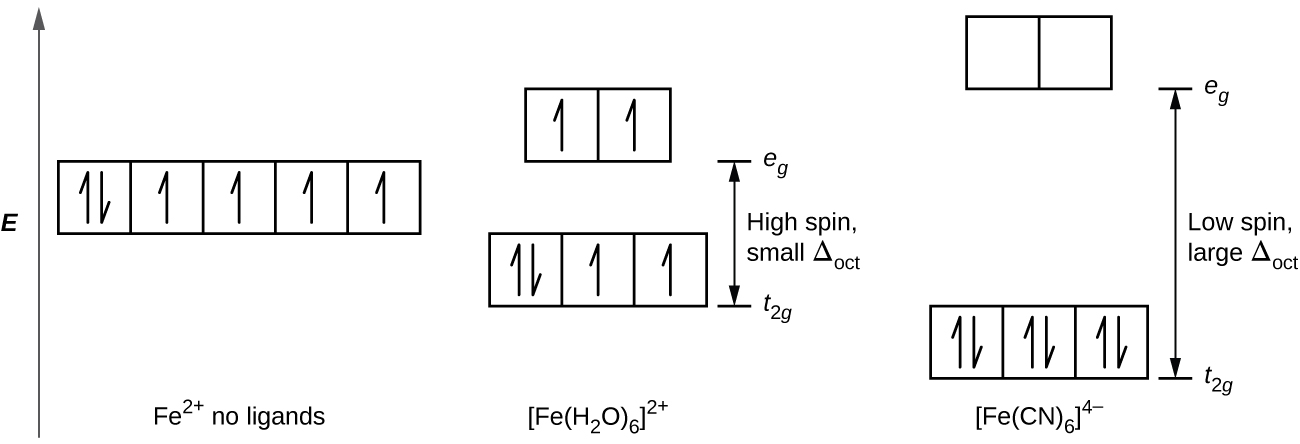
Iron(II) complexes have six electrons in the 5d orbitals. In the absence of a crystal field, the orbitals are degenerate. For coordination complexes with strong-field ligands such as [Fe(CN)6]4−, Δoct is greater than P, and the electrons pair in the lower energy t2g orbitals before occupying the eg orbitals. With weak-field ligands such as H2O, the ligand field splitting is less than the pairing energy, Δoct less than P, so the electrons occupy all d orbitals singly before any pairing occurs. Image used with permissin (CC- BY OpenStax).
Term Symbols
Term symbols are a shorthand method used to describe the angular momentum and spin multiplicities of an atom in a particular state. The ground state term symbol is predicted by Hund's rules. A term symbol takes the general form
\[^{2S+1}L_{J}\]
where
- \(S\) is the total spin angular momentum of the atom,
- \(L\) is the total orbital angular momentum and
- \(J\) is the total angular momentum of the atom .
Note that the total orbital angular momentum is represented by a letter. In analogy to the orbital angular momentum of single electrons where we have
- \(l = 0\) is \(s\)
- \(l = 1\) is \(p\);
- \(l = 2\) is \(d\)
- \(l = 3\) is \(f\)
For total orbital angular momentum we have
- \(L = 0\) is \(S\),
- \(L = 1\) is \(P\)
- \(L = 2\) is \(D\)
- \(L = 3\) is \(F\)
which derived from the characteristics of the spectroscopic lines corresponding to (s, p, d, f) orbitals. The first 17 symbols of \(L\) are
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| S | P | D | F | G | H | I | K | L | M | N | O | Q | R | T | U | V |
A typical term symbol might be
\[ \large ^2P_{3/2}\]
which is read as "doublet \(P\) three halves". The doublet indicates that \(S = 1/2\) since our setting the superscript \(2\) equal to \(2S + 1\) and solving for \(S\) yields \(S = 1/2\).
Note that all of the quantities that are involved in term symbols, S, L, and J, are vector quantities. In addition, note that this form of the term symbol implies that L and S are well defined quantities, i.e., that there are quantum numbers from which these values can be directly determined. What we mean here by well - defined quantities is that if a quantity is well defined then its value when measured will be one of several values which is stable for a substantial time. If the value is continually fluctuating it is not well defined. In general, for multielectron atoms this is not a valid assumption for L and S. In general, among the three quantities L, S, and J, only J will truly be an eigenvalue. In other words, we will be able to make observations that reflect the value of the total angular momentum J or which depend on there being a definite value of J, but not ones that yield L or S exactly. However, for the specific case of light atoms, where the atomic number Z < 40, L and S are so close to being well defined, that we can treat them as if they are.
What is the term for the excited state of hydrogen with the electron in a 2p orbital?
- Answer
-
This is a simple case since there is only one electron.

Orbital angular momentum
\[ L = \sum_i^n l = 1\]
since \(l\) for the 2p orbital is 1.
Spin momentum
\[S = 1/2\]
since there is only one electron
Total angular momentum
There are two possible total angular momenta possible (see Clebsch-Gordon series above).
\[ J = 1 + ½ = 3/2\]
and
\[J = 1 - ½ = 1/2\]
So there are two term symbols associated with this electron configuration
\(^2P_{1/2}\) and \(^2P_{3/2}\)
But which is associated with the ground-state? That required Hund's rules.
- Interpretation:
-
The ground state of the hydrogen atom corresponds to the electron configuration in which the electron occupies the 1s spatial orbital and can have either spin \(\alpha\) or spin \(\beta\). The term symbol for the ground state is \(^2 S_{1/2}\), which is read as “doublet S 1/2”. The spin quantum number is 1/2 so the superscript 2S+1 = 2, which gives the spin multiplicity of the state, i.e. the number of spin states equals 2 corresponding to \(\alpha\) and \(\beta\). The S in the term symbol indicates that the total orbital angular momentum quantum number is 0 (For the ground state of hydrogen, there is only one electron and it is in an s-orbital with \(l = 0\) ). The subscript ½ refers to the total angular momentum quantum number. The total angular momentum is the sum of the spin and orbital angular momenta for the electrons in an atom. In this case, the total angular momentum quantum number is just the spin angular momentum quantum number, ½, since the orbital angular momentum is zero. The ground state has a degeneracy of two because the total angular momentum can have a z-axis projection of \(+\frac {1}{2} \hbar\) or \(-\frac {1}{2} \hbar\), corresponding to \(m_J\) = +1/2 or -1/2 resulting from the two electron spin states \(\alpha\) and \(\beta\). We also can say, equivalently, that the ground state term or energy level is two-fold degenerate.
What is the term for the ground state of helium?
- Interpretation:
-
The electron configuration of the ground state of helium is 1s2 from the aufbau principle.
The combined orbital angular momentum is the sum of constituent orbital angular momenta
\[ L= L(1) + L(2) = 0 + 0 = 0\]
this is zero since the two electrons are in the ground state s orbital (\(l=0\).
Now, the spin part
\[ S = m_s(1) + m_s(2) = +1/2 - 1/2 = 0\]
Both spins are oppositely aligned since they are in the same orbital and the cancel. Now total angular momenta
\[ J= L + S = 0 + 0\]
Now switch to multiplicities
\[2S+1 = 2(0) + 1 = 1\]
and
\[J = L + S = 0\]
There is only one ground state term symbol
\[ ^1S_0\]
What are the possible term symbols for an \(1s^2s^22p^3\) electron configuration?
- Solution:
-
Among other combinations not shown.
We can ignore fully occupied subshells, because their contribution to \(M_L\) and \(M_S\) is zero. Thus we have enough information to solve this problem, only knowing the unfilled subshell.
\[L = 2,1,0\]
since \(M_L\) can be -2, -1, 0, 1, or 2.
Let's consider all permutations:
For \(L = 2\)
\(S = 1/2\) since there is one unpaired electron (the one in the \(m_l\) = 0 orbital). Thus
J = 5/2 or 3/2
So we have
\(^2D_{5/2}\) and \(^2D_{3/2}\).
For \(L = 1\)
\(S = 1/2\) since there is one unpaired electron (the one in the \(m_l\) = −1 or 1 orbital). Thus
J = 3/2, or 1/2.
So we also have
\(^2P_{3/2}\) and \(^2P_{1/2}\)
Finally, for L = 0
\(S = 3/2\) since all three electrons are unpaired (there is one in each of the \(m_l\) orbitals (-1, 0, and 1)).
J = 3/2.
So there is one more term symbol,
\(^4S_{3/2}\).
Summary of electronic structure of multi-electron atoms
The aim is to understand the experiment (in this case, how many energy levels are present in an atom) and not to predict the exact value of the energy levels.
- The first level of approximation is the independent electron approximation. Each electron is in an orbital and the energy is determined only by the orbital occupation or electronic configuration.
- The second level of approximation is considering that the energy is different if the total orbital angular momentum and spin angular momentum are different. We differentiate the energy in terms symbols depending on the values of L and S.
- The most accurate level takes into account the spin orbit coupling. The energy levels are identified by the total angular momentum J.


Last lecture addressed the consequence of indistinguishability in electronic structure calculations. The Hartree and Hartree-Fock (HF)caclulations were introduced within the Self-Consistent-Field (SCF) approach (similar to numerical evaluation of minima). The Hartree method treats electrons via only as an average repulsion energy and the HF approach using Slater determinant wavefunctions introduces an exchange energy term. Ionization energy and electron affinities are discussed within the context of Koopman's theorem.