3.11: Magnetic Behavior of Complex Ions
- Page ID
- 81695
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Discuss the correlation between the electronic structure of a coordination complex and its magnetic properties
Experimental evidence of magnetic measurements supports the theory of high- and low-spin complexes. Remember that molecules such as \(\ce{O2}\) that contain unpaired electrons are paramagnetic. Paramagnetic substances are attracted to magnetic fields. Many transition metal complexes have unpaired electrons and hence are paramagnetic. Molecules such as \(\ce{N2}\) and ions such as \(\ce{Na^{+}}\) and \(\ce{[Fe(CN)6]^{4−}}\) that contain no unpaired electrons are diamagnetic. Diamagnetic substances have a slight tendency to be repelled by magnetic fields.
When an electron in an atom or ion is unpaired, the magnetic moment due to its spin makes the entire atom or ion paramagnetic. The size of the magnetic moment of a system containing unpaired electrons is related directly to the number of such electrons: the greater the number of unpaired electrons, the larger the magnetic moment. Magnetic susceptibility measures the force experienced by a substance in a magnetic field. When we compare the weight of a sample to the weight measured in a magnetic field (Figure \(\PageIndex{1}\)), paramagnetic samples that are attracted to the magnet will appear heavier because of the force exerted by the magnetic field. We can calculate the number of unpaired electrons based on the increase in weight.
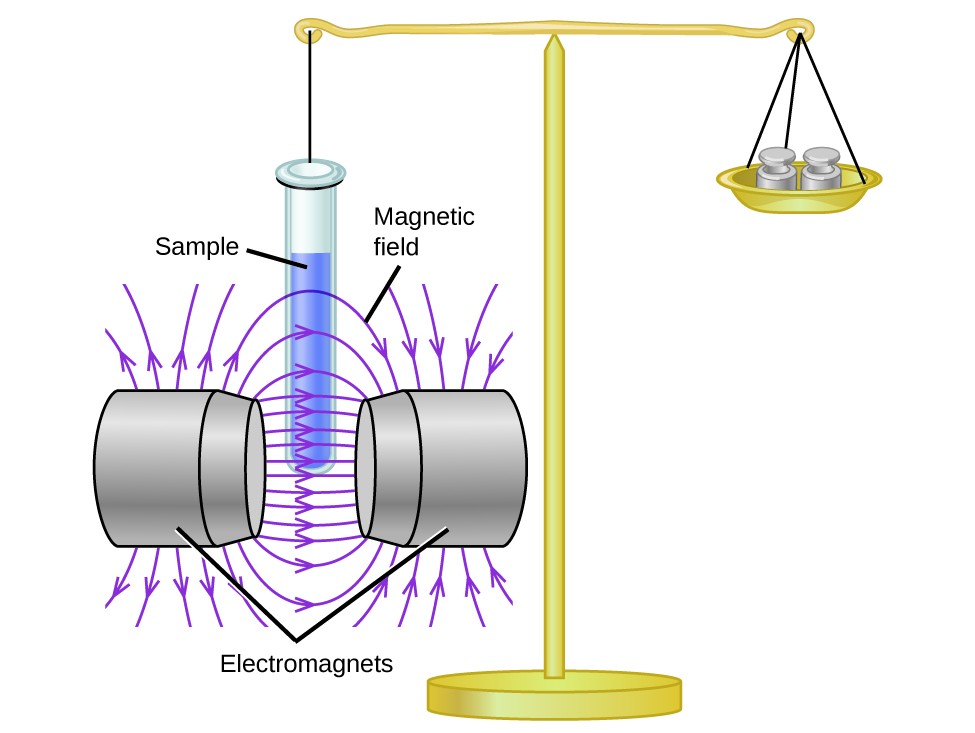
From this experiment, the measured magnetic moment of low-spin d6 \(\ce{[Fe(CN)6]{4−}}\) ion confirms that iron is diamagnetic, whereas the high-spin d6 [Fe(H2O)6]2+ complex has four unpaired electrons with a magnetic moment that confirms this arrangement. Therefore, the observed magnetic moment is used to determine the number of unpaired electrons present.
Magnetic Properties of Coordination Compounds
An interesting characteristic of transition metals is their ability to form magnets. Metal complexes that have unpaired electrons are magnetic. Since the last electrons reside in the d orbitals, this magnetism must be due to having unpaired d electrons. Considering only monometallic complexes, unpaired electrons arise because the complex has an odd number of electrons or because electron pairing is destabilized. For example, the Ti(III) ion has one d electron and must be (weakly) paramagnetic, regardless of the geometry or the nature of the ligands. However, the Ti(II) ion with two d-electrons, sometimes forms complexes with two unpaired electrons and sometimes forms complexes with no unpaired electrons.
As an example, Fe prefers to exist as \(\ce{Fe^{3+}}\) and is known to have a coordination number of six. Since the configuration of \(\ce{Fe^{3+}}\) has five d electrons, we would expect to see five unpaired spins in complexes with \(\ce{Fe}\). This is true for \(\ce{[FeF6]^{3-}}\); however, \(\ce{[Fe(CN)6]^{3-}}\) only has one unpaired electron, making it a weaker magnet. This trend can be explained based on the properties of the ligands. Based off the spectrochemical series, we expect \(\ce{CN^{-}}\) ligands to have a stronger electric field than that of \(\ce{F^{-}}\) ligands, so the energy differences in the d-orbitals should be greater for the cyanide complex.
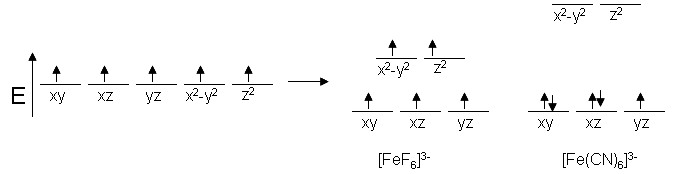
For this to make sense, there must be some sort of energy benefit to having paired spins for our cyanide complex (the spin pairing energy). That is, the energy level difference must be more than the repulsive energy of pairing electrons together. Since systems strive to achieve the lowest energy possible, the electrons will pair up before they will move to the higher orbitals. This is referred to as low spin, and an electron moving up before pairing is known as high spin.
Exercise \(\PageIndex{1}\)
Which ligand is most likely to form a high‐spin complexes when bound to transition metals: \(\ce{en}\), \(\ce{F^{‐}}\) , or \(\ce{CN^{‐}}\)?
- Answer
-
\(F^-\) are more likely to form high spin complexes, since is a weak-field ligand on the spectrochemical series.
Tetrahedral complexes have naturally weaker splitting because none of the ligands lie within the plane of the orbitals. As a result, they have either have too many or too few d electrons to warrant consideration about high or low spin configurations. Square planar compounds, on the other hand, stem solely from transition metals with eight d electrons. For example, \(\ce{[Ni(CN)4]^{2-}}\), \(\ce{[Pt(NH3)3Cl]^{+}}\), and \(\ce{[PtCl4]^{2-}}\) are all diamagnetic. Since this encompasses the full spectrum of ligand strength, we can conclude that square planar compounds are always low spin and therefore are weakly magnetic.
Example \(\PageIndex{2}\)
Which one of the following coordination compounds would you expect to be paramagnetic?
- \(\ce{[Zn(NH_3)_4]Cl_2}\)
- \(\ce{K[FeCl_4]}\) (low spin, tetrahedral)
- \(\ce{[Cd(H_2O)_6]SO_4}\)
Solution
Let's consider each compound individually. Since each compound has only one complex ion, we only need to consider how the d electrons are distributed in the ligand field of that ion. We can ignore the other parts (the counter ions) of the compound.
- The zinc ion in \(\ce{[Zn(NH_3)_4]Cl_2}\) has a +2 oxidation state, so it is a d10 ion since the zinc atom loses two 4s electrons and no 3d electrons to form the ion. We do not need to fill ion the electrons in the corresponding tetrahedral d-orbital diagram, since we know they will all be paired up. This is a diamagnetic compound.
- The iron ion in \(\ce{K[FeCl_4]}\) (low spin, tetrahedral) has a 3+ oxidation state so it is a d5 ion since the iron atom loses two 4s electrons and one 3d electron. Adding 5 electrons to the tetrahedral d-orbital diagram identifies that one electron will be unpaired. This compound will be paramagnetic (but weakly since only on electron is unpaired).
- The cadmium ion in \(\ce{[Cd(H_2O)_6]SO_4}\) has a +2 oxidation state, so it is a d10 ion since the cadmium atom loses two 5s electrons and no 4d electrons to form the ion. We do not need to fill ion the electrons in the corresponding octahedral d-orbital diagram, since we know they will all be paired up. This is a diamagnetic compound.
Exercise \(\PageIndex{2}\)
Predict the number of unpaired electrons for each of the following complex ions
- \(\ce{[Fe(CN)_6]^{4‐} }\)
- \(\ce{[Ru(NH_3)_6]^{3+} }\)
- \(\ce{[Cr(NH_3)_6]^{2+}}\)
- \(\ce{[EuCl_6]^{4‐}}\)
- Answer a
-
\(\ce{Fe^{2+}}\) is 3d6 ion and has 0 unpaired electron in low spin complexes
- Answer b
-
\(\ce{Ru^{3+}}\) is 4d5 ion and has 1 unpaired electron in low spin complexes
- Answer c
-
\(\ce{Cr^{2+}}\) is 4d4 ion and has 4 and 2 unpaired electrons in high spin and low spin complexes, respectively, depending on spin pairing energy
- Answer d
-
\(\ce{Eu^{2+}}\) is 4f7 ion and has 7 unpaired electrons in high spin complexes
In bi- and polymetallic complexes, in which the individual centers have an odd number of electrons or electrons are high-spin, the situation is more complicated. If there is interaction between the two (or more) metal centers, the electrons may couple, resulting in a weak magnet, or they may enhance each other. When there is no interaction, the two (or more) individual metal centers behave as if in two separate molecules.
Summary
- Unpaired electrons exist when the complex has an odd number of electrons or because electron pairing is destabilized.
- The more unpaired electrons, the stronger the magnetic property.
- Tetrahedral complexes have weaker splitting because none of the ligands lie within the plane of the orbitals.
- Square planar compounds are always low-spin and therefore are weakly magnetic.
- In bi- and polymetallic complexes, the electrons may couple through the ligands, resulting in a weak magnet, or they may enhance each other.
Contributors and Attributions
- Source: Boundless. "Magnetic Properties." Boundless Chemistry Boundless, 26 May. 2016. Retrieved 4 May. 2017 from www.boundless.com/chemistry/...ties-616-6882/.

