3.10: Magnetic Behavior of Atoms, Molecules, and Materials
- Page ID
- 48470
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- To understand the difference between Ferromagnetism, paramagnetism and diamagnetism
- To identify if a chemical will be paramagnetic or diamagnetic when exposed to an external magnetic field
The magnetic moment of a system measures the strength and the direction of its magnetism. The term itself usually refers to the magnetic dipole moment. Anything that is magnetic, like a bar magnet or a loop of electric current, has a magnetic moment. A magnetic moment is a vector quantity, with a magnitude and a direction. An electron has an electron magnetic dipole moment, generated by the electron's intrinsic spin property, making it an electric charge in motion. There are many different magnetic behavior including paramagnetism, diamagnetism, and ferromagnetism.
An interesting characteristic of transition metals is their ability to form magnets. Metal complexes that have unpaired electrons are magnetic. Since the last electrons reside in the d orbitals, this magnetism must be due to having unpaired d electrons. The spin of a single electron is denoted by the quantum number \(m_s\) as +(1/2) or –(1/2). This spin is negated when the electron is paired with another, but creates a weak magnetic field when the electron is unpaired. More unpaired electrons increase the paramagnetic effects. The electron configuration of a transition metal (d-block) changes in a coordination compound; this is due to the repulsive forces between electrons in the ligands and electrons in the compound. Depending on the strength of the ligand, the compound may be paramagnetic or diamagnetic.
Ferromagnetism (Permanent Magnet)
Ferromagnetism is the basic mechanism by which certain materials (such as iron) form permanent magnets. This means the compound shows permanent magnetic properties rather than exhibiting them only in the presence of an external magnetic field (Figure \(\PageIndex{1}\)). In a ferromagnetic element, electrons of atoms are grouped into domains in which each domain has the same charge. In the presence of a magnetic field, these domains line up so that charges are parallel throughout the entire compound. Whether a compound can be ferromagnetic or not depends on its number of unpaired electrons and on its atomic size.
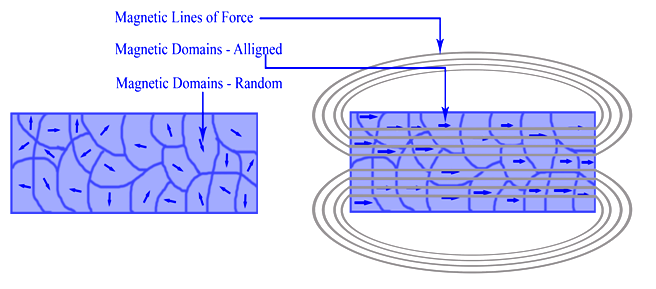
Ferromagnetism, the permanent magnetism associated with nickel, cobalt, and iron, is a common occurrence in everyday life. Examples of the knowledge and application of ferromagnetism include Aristotle's discussion in 625 BC, the use of the compass in 1187, and the modern-day refrigerator. Einstein demonstrated that electricity and magnetism are inextricably linked in his theory of special relativity.
Paramagnetism (Attracted to Magnetic Field)
Paramagnetism refers to the magnetic state of an atom with one or more unpaired electrons. The unpaired electrons are attracted by a magnetic field due to the electrons' magnetic dipole moments. Hund's Rule states that electrons must occupy every orbital singly before any orbital is doubly occupied. This may leave the atom with many unpaired electrons. Because unpaired electrons can spin in either direction, they display magnetic moments in any direction. This capability allows paramagnetic atoms to be attracted to magnetic fields. Diatomic oxygen, \(O_2\) is a good example of paramagnetism (described via molecular orbital theory). The following video shows liquid oxygen attracted into a magnetic field created by a strong magnet:
Diamagnetism (Repelled by Magnetic Field)
As shown in the video, molecular oxygen (\(\ce{O2}\)) is paramagnetic and is attracted to the magnet. In contrast, molecular nitrogen (\(\ce{N_2}\)) has no unpaired electrons and is diamagnetic; it is unaffected by the magnet. Diamagnetic substances are characterized by paired electrons, e.g., no unpaired electrons. According to the Pauli Exclusion Principle which states that no two electrons may occupy the same quantum state at the same time, the electron spins are oriented in opposite directions. This causes the magnetic fields of the electrons to cancel out; thus there is no net magnetic moment, and the atom cannot be attracted into a magnetic field. In fact, diamagnetic substances are weakly repelled by a magnetic field as demonstrated with the pyrolytic carbon sheet in Figure \(\PageIndex{2}\).

How to Tell if a Substance is Paramagnetic or Diamagnetic
The magnetic properties of a substance can be determined by examining its electron configuration: If it has unpaired electrons, then the substance is paramagnetic and if all electrons are paired, the substance is then diamagnetic. This process can be broken into three steps:
- Write down the electron configuration
- Draw the valence orbitals
- Identify if unpaired electrons exist
- Determine whether the substance is paramagnetic or diamagnetic
Example \(\PageIndex{1}\): Chlorine Atoms
Step 1: Find the electron configuration
For Cl atoms, the electron configuration is 3s23p5
Step 2: Draw the valence orbitals
Ignore the core electrons and focus on the valence electrons only.
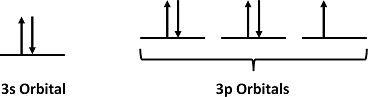
Step 3: Look for unpaired electrons
There is one unpaired electron.
Step 4: Determine whether the substance is paramagnetic or diamagnetic
Since there is an unpaired electron, \(\ce{Cl}\) atoms are paramagnetic (albeit, weakly).
Example \(\PageIndex{2}\): Zinc Atoms
Step 1: Find the electron configuration
For Zn atoms, the electron configuration is 4s23d10
Step 2: Draw the valence orbitals
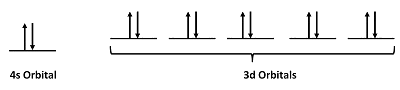
Step 3: Look for unpaired electrons
There are no unpaired electrons.
Step 4: Determine whether the substance is paramagnetic or diamagnetic
Because there are no unpaired electrons, \(\ce{Zn}\) atoms are diamagnetic.
Exercise \(\PageIndex{1}\)
- How many unpaired electrons are found in oxygen atoms ?
- How many unpaired electrons are found in bromine atoms?
- Indicate whether boron atoms are paramagnetic or diamagnetic.
- Indicate whether \(\ce{F^{-}}\) ions are paramagnetic or diamagnetic.
- Indicate whether \(\ce{Fe^{2+}}\) ions are paramagnetic or diamagnetic.
- Answer a
- The O atom has 2s22p4 as the electron configuration. Therefore, O has 2 unpaired electrons.
- Answer b
- The Br atom has 4s23d104p5 as the electron configuration. Therefore, Br has 1 unpaired electron.
- Answer c
- The B atom has 2s22p1 as the electron configuration. Because it has one unpaired electron, it is paramagnetic.
- Answer d
- The \(\ce{F^{-}}\) ion has 2s22p6 as the electron configuration. Because it has no unpaired electrons, it is diamagnetic.
- Answer e
- The \(\ce{Fe^{2+}}\) ion has 3d6 as the electron configuration. Because it has 4 unpaired electrons, it is paramagnetic.
References
- Pettrucci, Ralph H. General Chemistry: Principles and Modern Applications. 9th. Upper Saddle River: Pearson Prentice Hall, 2007
- Sherman, Alan, Sharon J. Sherman, and Leonard Russikoff. Basic Concepts of Chemistry Fifth Edition. Boston, MA: Houghton Mifflin Company, 1992. Print.

