Expanded Lecture 25: Molecules and Molecular Orbital Theory
- Page ID
- 40115
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Last lecture address how the different orbital angular momenta of multi-electron atoms couple to break degeneracies predicted from the "Ignorance is Bliss" approximation (i.e., the hydrogen atom). Total angular momenta are introduced along with multiplicity. Atomic term symbols are discussed along with all three of Hund rules to identify the most stable combination of angular momenta for a specific electron configuration.
Spin-Orbit Coupling (Different Angular Momenta Combinations have different Energies)
The angular momentum manipulations and in particular determining microstates for a specific electron configuration with characteristic term symbols did not suggest these different microstates affected the energy of a multi-electron system. For that to occur the spin must appear in the Hamiltonian.
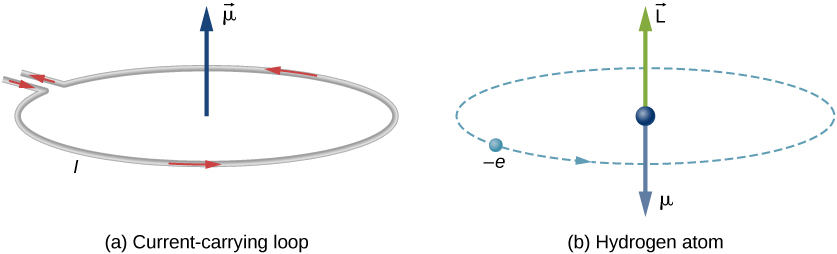
An electron that orbits the nucleus induces a "current" and a magnetic field. Similarly, the rotating electron (really intrinsic spin) of the electron induces a different magnet. Both a magnetic (dipole) moments will interact with each other via spin-orbit coupling to generate fine structure atomic spectra. (CC BY-SA OpenStax).
Each type of angular momentum generates magnetic dipoles that interacts:

The orbital angular momentum generates magnetic dipoles that interacts with the magnetic dipole of the spin angular momentum. This is spin-orbit coupling.
There is a very small term in the Hamiltonian that depends on the spin and this is called the spin-orbit coupling (which will not be written explicitly). Spin orbit coupling is important only for heavy atoms or when very accurate energy levels are needed (spectroscopy). The effect of spin orbit coupling is to split the spectroscopic terms in energy levels. The number of energy levels originating from a spectroscopic term is given by the possible values of the total angular momentum J = L + S (orbital plus spin angular momenta) with eigenfunction
\[\hat{\mathbf{J}}^2 | \psi \rangle = \hbar^2 J(J+1)| \psi \rangle \]
The quantum number \(J\) can take the values |L - S|, |L - S|+1, ..., L + S.
The spectroscopic term 3P (L=1, S=1) can have J=0,1,2 and therefore 3 finely spaced energy levels indicated as 3P0, 3P1, 3P2.
The energies of the terms depend upon spin-orbit coupling and relativistic corrections that need to be included in the Hamiltonian operator in order to provide a more complete description of the hydrogen atom. As a consequence of these effects, all terms with the same n and J quantum numbers have the same energy while terms with different values for n or J have different energies.
Hund's Rules Can be used to Identify Ground State Combination
Hund’s Rules tell us how to determine the ground state of a configuration based on its term symbols.
- Hund's Rule #1. The state with the larger value of S (higher multiplicity) is more stable. MAXIMIZE TOTAL SPIN ANGULAR MOMENTUM
Hund's first rule states that the lowest energy atomic state is the one that maximizes the total spin quantum number (\(S = \sum_i\)) for the electrons in the open subshell. The orbitals of the subshell are each occupied singly with electrons of parallel spin before double occupation occurs. The reason is that the electrons in singly occupied orbitals are less effectively screened or shielded from the nucleus, so that such orbitals contract and electron–nucleus attraction energy becomes greater in magnitude
The electronic configuration of Carbon is 1s2 2s2 2p2.
- Answer
-
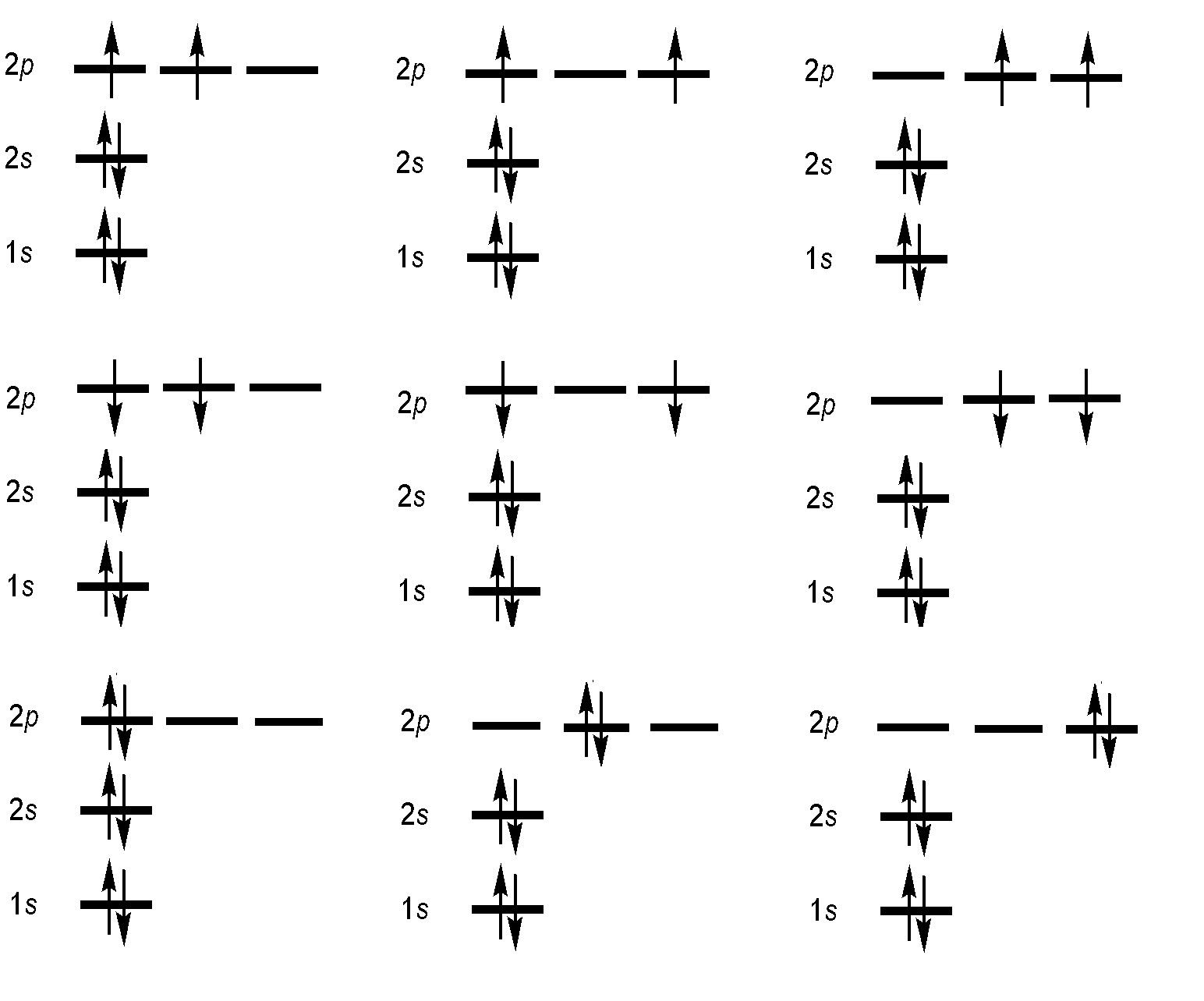
We need to consider only the outer 2p2 electrons, for which it can be shown that the possible terms (ignoring \(J\)) allowed by the Pauli exclusion principle are
1D , 3P , and 1S.
Hund's first rule now states that the ground state term is 3P (triplet P), which has \(S = 1\). The superscript 3 is the value of the multiplicity
\[2S + 1 = 3\]
However, Hund's rule #1 doesn't address the optimal \(M_L\) values. That requires the other Hund's rule to address.
- Hund's Rule #2. For states with the same \(S\), the one with the larger \(L\) is more stable. MAXIMIZE TOTAL ORBITAL ANGULAR MOMENTUM
This rule deals with reducing the repulsion between electrons. It can be understood from the classical picture that if all electrons are orbiting in the same direction (higher orbital angular momentum) they meet less often than if some of them orbit in opposite directions. In the latter case the repulsive force increases, which separates electrons. This adds potential energy to them, so their energy level is higher.
Electronic Configuration: 1s2 2s2 2p6 3s2 3p6 3d2 4s2.
- Answer
-
In this case the open shell is 3d2 and the allowed terms include three singlets (1S, 1D, and 1G) and two triplets (3P and 3F). (Here the symbols S, D, G, P and F indicate that the total orbital angular momentum quantum number has values 0, 2, 4, 1 and 3 respectively.)
We deduce from Hund's first rule that the ground state is one of the two triplets, and from Hund's second rule that the ground state is 3F (with \({ L=3}\)) rather than 3P (with \({ L=1}\)).
- Hund's Rule #3. For states with the same S and L:
- if subshell is half-filled or less, the smaller \(J\) is more stable
- if subshell is more than half filled, the larger \(J\) is more stable
What is term symbol for the ground state of Silicon?
- Answer
-
From Hund's rule #1 we idenify that the ground-state term (addressing \(L\) and \(S\)) is 3P
However, The \({ {}^{3}\!P\,}\) lowest energy term of Si consists of three \(J|) levels since \(\L=1\) and \(S=1\). So \({ J=2,1,0\,}\).
With only two of six possible electrons in the shell, it is less than half-full and thus \({ {}^{3}\!P_{0}\,}\) is the ground state.
Zr has a ground state configuration of \([Kr]4d^25s^2\). What is its ground-state term symbol?
- Answer
-
We only need to concern ourselves with the unfilled subshell (\(4d^2\)). Why?
Hund's Rule #1:
We are looking for the highest multiplicity, thus as many spins as possible should be parallel. This is when \(S=1\) or the system is a doublet (\(2S+1\)).
Hund's Rule #2:
Find the states with the highest \(L\). This is when the two electrons are in the \(m_l=1\) p-orbital and the \(m_l =1\) p-orbital.
Since \(S = 1\) and \(L = 3\), \(J\) can be 4, 3, or 2. Which is preferred?
Hund's Rule #3
Since this subshell is less than half full, the preferred state is with a minimized \(J\), which is \(J=2\) in this case.
The ground-state term symbol for the ground-state of Zirconium is
\[^2F_2\]
Summary of electronic structure of multi-electron atoms
The aim is to understand the experiment (in this case, how many energy levels are present in an atom) and not to predict the exact value of the energy levels.
- The first level of approximation is the independent electron approximation. Each electron is in an orbital and the energy is determined only by the orbital occupation or electronic configuration.
- The second level of approximation is considering that the energy is different if the total orbital angular momentum and spin angular momentum are different. We differentiate the energy in terms symbols depending on the values of L and S.
- The most accurate level takes into account the spin orbit coupling. The energy levels are identified by the total angular momentum J.
A bit more about Atoms and Spectroscopy (and Another selection rule)
The H-alpha (\(H_α\)) line of Hydrogen is a specific deep-red visible spectral line in the Balmer series created by hydrogen with a wavelength of 656.28 nm, which occurs when a hydrogen electron falls from its third to second lowest energy level.
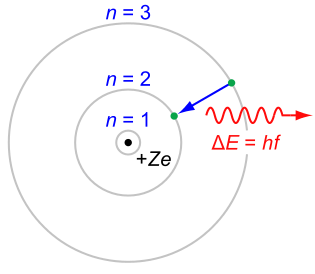
H-alpha Emission: In the simplified Rutherford Bohr model of the hydrogen atom, the Balmer lines result from an electron jump between the second energy level closest to the nucleus, and those levels more distant. from Wikipedia.
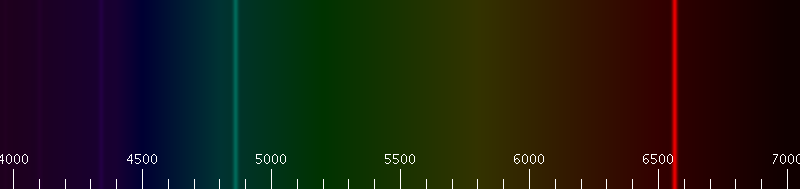

This is explained in terms of the different term symbols (also called fine structure). A portion of the hydrogen atom transition level diagram for optical spectra then, will look like
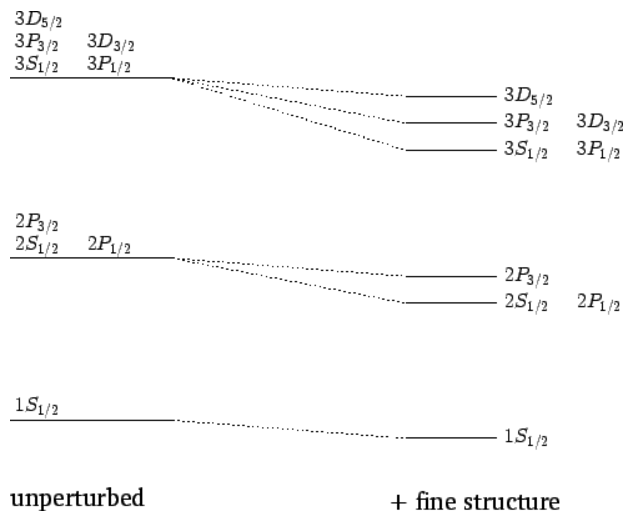
Effect of the fine structure energy-shift on the n=1,2, and 3 states of a hydrogen atom. Not to scale.
New Selection Rules for electronic Spectra
Before we outlined the section rules for atomic transitions. Now, we can expand it to take into account electron spin (and total spin) issues:
Before we had only two selection rules for electronic spectroscopy
- ∆n can be anything (not much of a rule)
- ∆l = ±1
- \(∆m_l\) = ±1 and 0
Now, once we introduce spin-orbit coupling that results in fine structure, we can introduce a couple more:
- ∆S = 0
- ∆J = 0, ±1 except the \(J = 0 \rightarrow J = 0\),w hich is not observed
Drop the original \(∆m_l\) requirement, since that is folded into the new \(∆J\) selection rule
Which transitions is not allowed in the following fine structure?
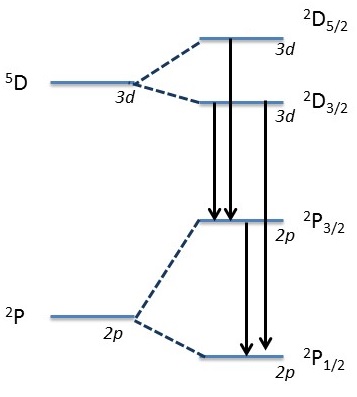
List all of the allowed transitions between the sodium states \(^2S_{1/2}\), \(^2P_{3/2}\), \(^2P_{1/2}\), \(^2D_{3/2}\), \(^2D_{1/2}\), \(^2F_{7/2}\), and \(^2F_{5/2}\).
- Answer
-
This requires asking which possible transitions are possible via the selection rules outlined above.
.
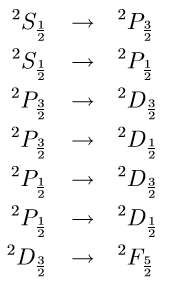
The rest are not allowed? For example
\(^2S_{1/2} \rightarrow ^2D_{3/2}\) is not allowed since \(\Delta L =2\) and \(^2S_{3/2} \rightarrow ^2D_{7/2}\) is not allowed since \(\Delta J =2\).
Back to Born-Oppenheimer Approximation
We will consider a very general molecule with \(N\) nuclei and \(M\) electrons. The coordinates of the nuclei are \(R_1 ,...,R_N\). The coordinates of the electrons are \(r_1 ,...,r_M\), and their spin variables are \(S_{z,1},...,S_{z,M}\). For shorthand, we will denote the complete set of nuclear coordinates as \(R\) and the set of electrons coordinates as \(r\) and \(x\) the complete set of electron coordinates and spin variables. The total molecular wave function \(\psi (x,R)\) depends on \(3N+4M\) variables, which makes it a very cumbersome object to deal with. The Born-Oppenheimer approximation leads to a very important simplification of the wave function.
Nuclei move and electrons adjust quickly.
If we could neglect the electron-nuclear interaction, then the wave function would be a simple product \(\psi (x,R)=\psi_{elec}(r)\psi_{nucl}(R)\). However, we cannot neglect this term, but it might still be possible to write the wave function as a product. We note, first, that most nuclei are 3-4 orders of magnitude heaver than an electron. For the lightest nucleus, the proton,
\[m_p \approx 2000 m_e\]
This mass difference is large enough to have important physical consequences. Let us think classically about this mass difference first. If two particles interact in some way, and one is much heavier than the other, the light particle will move essentially as a ``slave'' of the heavy particle. That is, it will simply follow the heavy particle wherever it goes, and, it will move rapidly in response to the heavy particle motion. As an illustration of this phenomenon, consider the simple mechanical system pictured below:
![\includegraphics[scale=0.5]{Adiabatic_springs.eps}](http://www.nyu.edu/classes/tuckerman/adv.chem/lectures/lecture_13/img13.png)
Considering this as a classical system, we expect that the motion will be dominated by the large heavy particle, which is attached to a fixed wall by a spring. The small, light particle, which is attached to the heavy particle by a spring will simply follow the heavy particle and execute rapid oscillations around it.
So a good approximation is to describe the electronic states of a molecule by thinking that the nuclei are not moving, i.e. that they are stationary. The nuclei, however, can be stationary at different positions so the electronic wavefunction can depend on the positions of the nuclei even though their motion is neglected.
Now we look at the mathematics to see what is done in solving the Schrödinger equation after making the Born-Oppenheimer approximation. For a diatomic molecule as an example, the Hamiltonian operator is grouped into three terms
\[\hat {H} (r, R) = \hat {T}_{nuc} (R) + \dfrac {e^2}{4\pi \epsilon _0} \dfrac {Z_A Z_B}{R} + \hat {H} _{elec} (r,R)\]
where
\[T_{nuc} (R) = -\dfrac {\hbar^2}{2m_A} \nabla ^2_A - \dfrac {\hbar ^2}{2m_B} \nabla ^2_B \]
and
\[\hat {H} _{elec} (r, R) = \dfrac {- \hbar ^2}{2m} \sum \limits _i \nabla ^2_i + \dfrac {e^2}{4 \pi \epsilon _0} \left ( -\sum \limits _i \dfrac {Z_A}{r_{Ai}} - \sum \limits _i \dfrac {Z_B}{r_{Bi}} + \dfrac {1}{2} \sum \limits _i \sum \limits _{j \ne i} \dfrac {1}{r_{ij}}\right ) \]
he Born-Oppenheimer approximation says that the nuclear kinetic energy terms in the complete Hamiltonian can be neglected in solving for the electronic wavefunctions and energies. Consequently, the electronic wavefunction \(\varphi _e (r,R)\) is found as a solution to the electronic Schrödinger equation
\[\hat {H} _{elec} (r, R) \varphi _e (r, R) = E_e (R) \varphi _e (r, R) \]
The mass of an electron is 1860 times less than that of a proton. This is a crucial difference since it permits us to treat the electrons as a wave function while treating the nuclear positions as fixed. In effect, the nuclei are not being treated using the wave-like properties. If they were then we would need to solve two simultaneous wave equations in order to describe even the simplest atom. The mass difference also leads to a difference in time scale for motion, which is the fundamental physical reason that the approximation holds.

