14: Harmonic Oscillators and IR Spectroscopy
- Page ID
- 94024
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Because of the association of the wavefunction with a probability density, it is necessary for the wavefunction to include a normalization constant, \(N_v\).
\[N_v = \dfrac {1}{(2^v v! \sqrt {\pi} )^{1/2}} \label {5.6.15}\]
The final form of the harmonic oscillator wavefunctions is the product of three terms:
\[ \color{red} | \psi _v (x) \rangle = N_v H_v (\alpha x) e^{-\alpha x^2/2} \label {5.6.16}\]
The first few physicists' Hermite polynomials are:
- \(H_0(x)=1\,\)
- \(H_1(x)=2x\,\)
- \(H_2(x)=4x^2-2\,\)
- \(H_3(x)=8x^3-12x\,\)
- \(H_4(x)=16x^4-48x^2+12\,\)
- \(H_5(x)=32x^5-160x^3+120x\,\)
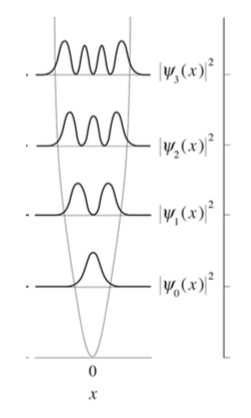
The symmetry of the Harmonic Oscillator wavefunctions is dictated by the Hermite Polynomials
- Which levels are even functions and which are odd functions?
- Without calculating an integral, what is \(\langle x\rangle\)?
We ended class on Wednesday discussing the symmetries of productions of functions that have symmetries.
| Product table | Odd Function (anti-symmetric) | Even Function (symmetric) | No symmetry (neither odd nor even) |
|---|---|---|---|
| Odd Function (anti-symmetric) | Even Function (symmetric) | Odd Function (anti-symmetric) | who knows |
| Even Function (symmetric) | Odd Function (anti-symmetric) | Even Function (symmetric) | who knows |
| No symmetry (neither odd nor even) | who knows | who knows | who knows |
The wavefunctions in Equation \ref{5.6.16} are the time-independent parts to the total wavefunction. As discussed previously, the total time-dependent wavefunctions can be expressed (if no time dependent potential is used as)
\[ | \Psi_v(x,t) \rangle = | \psi_v(x) \rangle e^{-iEt/\hbar}\]
Where \(v\) is the Harmonic oscillator quantum number (i.e. how excited the vibration is). This means that there is both a real and imaginary component to the wavefunction as it oscillates in time.
\[ | \Psi_v(x,t) \rangle = | \psi_v(x) \rangle \cos \left(Et/\hbar\right) - i | \psi_v(x) \rangle \sin \left(Et/\hbar \right) \]
This is visualized below.
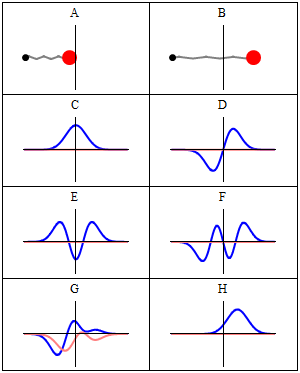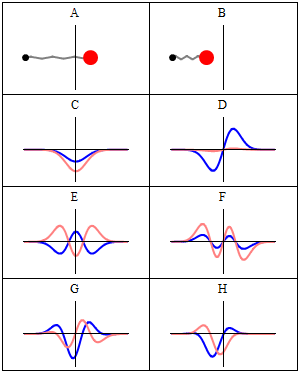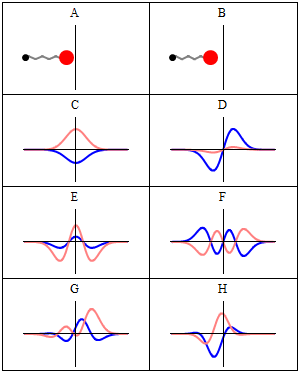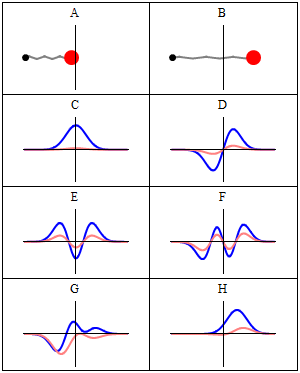
When can a vibration transition be IR active (within HO approximation)?
This is done via the transition moment integral \(\langle \psi_i | \hat{M}| \psi_f \rangle \). The transition moment integral gives information about the probability of a transition occurring. For IR of a single harmonic oscillator, \(\hat{M}\) can be set to \(x\). A more detailed discussion will be presented later. So the probability for a transition in HO is
\[P_{i \rightarrow f} = \langle \psi_i | x | \psi_f \rangle\]
- When the vibration has a changing dipole moment
- When the adjacent eigenstates \(v'=v\pm 1\) are involved (no harmonics or overtones)
Overtones are actually experimentally observed
Overtones occur when a vibrational mode is excited from \(\nu=0\) to \(\nu=2\), which is called the first overtone, or \(\nu=0\) to \(\nu=3\), the second overtone. The fundamental transitions, v=±1, are the most commonly occurring, and the probability of overtones rapid decreases as \(\nu=\pm n\) increases. Based on the harmonic oscillator approximation, the energy of the overtone transition will be about n times the fundamental associated with that particular transition. The anharmonic oscillator calculations show that the overtones are usually less than a multiple of the fundamental frequency. This is demonstrated with the vibrations of the diatomic HCl in the gas phase:
| Transition | ṽobs [cm-1] | ṽobs Harmonic [cm-1] | ṽobs Anharmonic [cm-1] |
|---|---|---|---|
| \( 0 \rightarrow 1 \) (fundamental) | 2,885.9 | 2,885.9 | 2,885.3 |
| \( 0 \rightarrow 2 \) (first overtone) | 5,668.0 | 5,771.8 | 5,665.0 |
| \( 0 \rightarrow 3 \) (second overtone) | 8,347.0 | 8,657.7 | 8,339.0 |
| \( 0 \rightarrow 4\) (thirdovertone) | 10,923.1 | 11,543.6 | 10,907.4 |
| \( 0 \rightarrow 5\) (fourth overtone) | 13,396.5 | 14,429.5 | 13,370 |
We can see from Table 1, that the anharmonic frequencies correspond much better with the observed frequencies, especially as the vibrational levels increase.
The Harmonic Oscillator is just an approximation of the True Potential
The Taylor series for an arbitrary potential energy curve \(V(x)\) is defined by:
\[ V(x) = U(x_0) + (x-x_0) \left.\dfrac{dV}{dx}\right|_{x_0} + \dfrac{(x-x_0)^2}{2!} \left.\dfrac{d^2V}{dx^2}\right|_{x_0} + \cdots \label{tay1}\]
The system will tend to settle into the configuration where \(U(x)\) has a minimum --- but, by definition, that's where the first derivative \(dV/dx=0\) vanishes. Also a constant offset to a potential energy usually does not affect the physics. That leaves us with
\[V(x) = \dfrac{(x-x_0)^2}{2!} \left.\dfrac{d^2V}{dx^2}\right|_{x_0} + \mathcal O(x-x_0)^3 \approx \dfrac12 k (x-x_0)^2 \label{tay2}\]
which is the harmonic oscillator potential for small oscillations around \(x_o\).

If the cubic term is not ignored, then the expansion can be rewritten as (taking the first two important terms of Equation \(\ref{tay1}\))
\[V(x) = \cancelto{0}{V(x_o)} + \dfrac {1}{2} k(x-x_o)^2 + \dfrac {1}{6} \gamma (x-x_o)^3 \label{tay3}\]
where
- \(V(\ell_0) = 0\) since we can define our zero.
- \(k\) is the harmonic force constant, and
- \(\gamma\) is the anharmonic term.
\(V(\ell)\) is typically shortened to the cubic term (but not always). It is important to note that this approximation is only good for \(\ell\) near \(\ell_0\), and that \(\ell_0\) stands for the equilibrium bond distance. Almost all diatomics have experimentally determined \(\dfrac {d^2 V}{d \ell^2}\) for their lowest energy states. H2, Li2, O2, N2, and F2 have had terms up to \(n < 10\) determined.
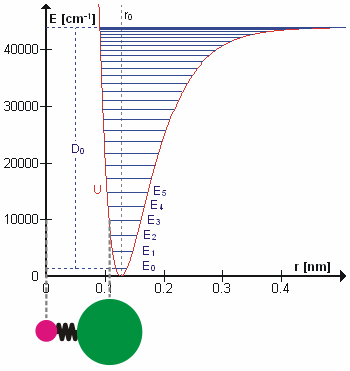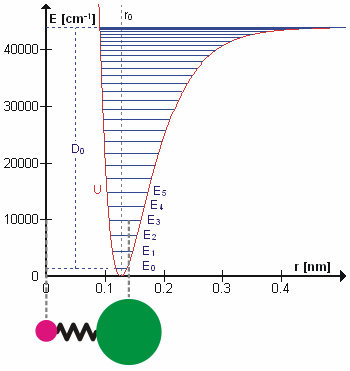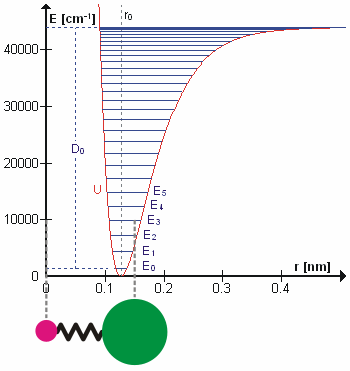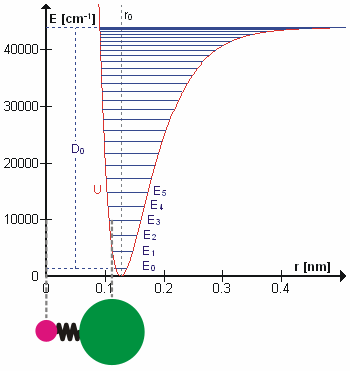
The Morse Potential (a better potential for describing Vibrations)
The Morse potential, named after physicist Philip M. Morse, is a convenient interatomic interaction model for the potential energy of a diatomic molecule. It is a better approximation for the vibrational structure of the molecule than the quantum harmonic oscillator because it explicitly includes the effects of bond breaking, such as the existence of unbound states. It also accounts for the anharmonicity of real bonds and the non-zero transition probability for overtone and combination bands.
The Morse Potential is a good approximation to \(V(\ell)\) and is best when looking for a general formula for all \(\ell\) from 0 to \(\infty\), not just applicable for the local region around the \(\ell_o\):
\[V(\ell) = D(1-e^{-\beta (\ell - \ell_0)})^2 \label{2}\]
with
- \(V(\ell = \ell_0) = 0\) and
- \(V(\ell = \infty) = D\)
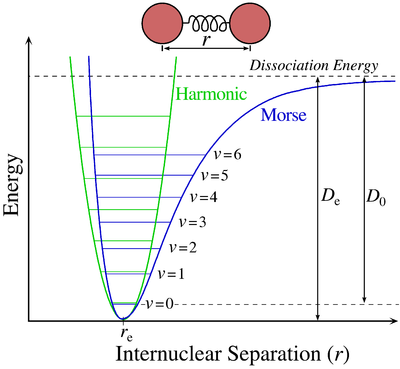
For H2, the equilibrium bond length \(\ell_0 = 74.1 pm\), the bond energy \(D = 7.61 \times 10^{-19} J\), and the Morse potential parameter \(\beta = 0.0193 pm^{-1}\).
To solve for energy using the relevant formulas \(\hat{H} \psi = E\psi\) and \(E = K + V\), an approximation must be made, saying that \(V(x) = \dfrac {1}{2} kx^2\). The kinetic energy is known because the motion is one dimensional, so the kinetic energy operator \(\hat{K}\) in the Particle in the Box problem can be used. The equation
\[\hat{H} \psi = E\psi \nonumber\]
now becomes
\[\hat{H} \psi = -\dfrac {\hbar^2}{2\mu} \dfrac {d^2 \psi}{d x^2} + \dfrac {1}{2}kx^2 = E\psi. \label{3}\]
Note that \(\mu\) is used as the reduced mass, not \(m\). For a diatomic molecule,
\[\mu = \dfrac {m_1 m_2}{m_1 + m_2}\]
Solving for the energy gives quantized results in terms of \(v\) - \(E_v = \hbar (\sqrt {\dfrac {k}{\mu}}) (v+ \dfrac {1}{2})\), which can be simplified to \(E_v = h\tilde{v} (v+\dfrac {1}{2})\), having \(cm^{-1}\) units.
Contributors and Attributions
David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski ("Quantum States of Atoms and Molecules")
William Reusch, Professor Emeritus (Michigan State U.), Virtual Textbook of Organic Chemistry



Lecture 13
Last lecture laid the groundwork for understanding spectroscopy. We first introduced bra-ket notation as a means to simplify the manipulation of integrals. We introduced a qualitative discussion of IR spectroscopy and then focused on "selection rules" for what vibrations are "IR-active" and can be seen in IR spectra. The two criteria we got were that the vibration requires a changing dipole moment (a static dipole is not needed as discussed for \(\ce{CO2}\)) and that \(\Delta v = \pm 1\) for the transition. We were setting the ground work for explaining how to derive the second selection rule using the concept of a transition moment and symmetry. We will pick up that discussion there.
Selection Rules and How to be a Couch Potato
Photons can be absorbed or emitted, and the harmonic oscillator can go from one vibrational energy state to another. Which transitions between vibrational states are allowed? If we take an infrared spectrum of a molecule, we see numerous absorption bands, and we need to relate these bands to the allowed transitions involving different normal modes of vibration.
The selection rules are determined by the transition moment integral. For IR Spectroscopy that is the dipole moment operator \(\hat{\mu}\):
\[ \begin{align} \mu_T &= \int \limits _{-\infty}^{\infty} \psi_{v'}^* (Q) \hat {\mu} (Q) \psi _v (Q) dQ \\[4pt] &= \langle \psi_{v'} |\hat {\mu} |\psi _v \rangle \label {6.6.1} \end{align}\]
To evaluate this integral we need to express the dipole moment operator, \(\hat {\mu}\), in terms of the magnitude of the normal coordinate \(Q\). Evaluating the integral in Equation \(\ref{6.6.1}\) can be difficult depending on the complexity of the wavefunctions used. We can often (although not always) take advantage of the symmetries of the wavefunction (and \(\hat {\mu}\) too) to make things easier.
While functions exhibit this symmetry, the product of functions inherit the symmetries of the constituent components via a "product table." The one below is in terms of odd/even symmetry, but as you will learn in other classes (especially group theories), there are several symmetries that 3D objects have. The product tables constructed that take into account all such symmetries are more complicated.
These symmetries are important since the integrand of an integral (over all space) of an odd function is ALWAYS zero. So you do not need to solve it.
Back to the Harmonic Oscillator Wavefunctions