13: Harmonic Oscillators and Rotation of Diatomic Molecules
- Page ID
- 39476
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Last lecture addressed three aspects. The first is the introduction of the commutator which is meant to evaluate if two operators commute (a property used extensively in basic algebra courses). Not every pair of operators will commute meaning the order of operations matter. The second aspect is to redefine the Heisenberg Uncertainty Principle now within the context of commutators. Now, we can identify if any two quantum measurements (i.e., eigenvalues of specific operators) will require the Heisenberg Uncertainty Principle to be addressed when simultaneously evaluating them. The third aspect of the lecture was the introduction of vibrations, including how many vibrations a molecule can have (depending on linearity) and the origin of this. The solutions to the harmonic oscillator potential were qualitatively shown (via Java application) with an emphasis of the differences between this model system and the particle in the box (important).
| Atoms (very symmetric) | Linear molecules (less symmetric) | Non-linear molecules (least symmetric) | |
|---|---|---|---|
| Translation (x, y, and z) | 3 | 3 | 3 |
| Rotation (x, y, and z) | 0 | 2 | 3 |
| Vibrations | 0 | 3N − 5 | 3N − 6 |
| Total (including Vibration) | 3 | 3N | 3N |
Last lecture laid the groundwork for understanding spectroscopy. We first introduce bra-ket notation as a means to simplify the manipulation of integrals. We introduced a qualitative discussion of IR spectroscopy and then focused on "selection rules" for what vibrations are "IR-active" and can be seen in IR spectra. The two criteria we got were that the vibration requires a changing dipole moment (a static dipole is not needed as discussed for \(CO_2\)) and that \(\Delta v = \pm 1\) for the transition. We were setting the ground work for explaining how to derive the second selection rule using the concept of a transition moment and symmetry. We will pick up that discussion there.
Quantum Mechanical Vibrations
The simplified potential discussed in general chemistry is the potential energy function used in constructing the Hamiltonian. From solving the Schrodinger equations, we get eigenfunctions, eigenvalues (energies) and quantum numbers. Combining these on the potential like we did for the particle in a box give a more detailed (quantum) picture
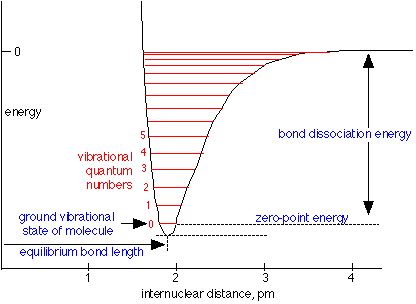
Zero-point energy
Zero-point energy is the lowest possible energy that a quantum mechanical system may have,i.e. it is the energy of the system's ground state. The uncertainty principle states that no object can ever have precise values of position and velocity simultaneously.
For the particle in the 1D box of length \(L\), with energies
\[E_n = \dfrac{h^2 n^2 }{8m L^2}\]
the zero-point energy (\(n=1\)) is
\[E_{ZPE} = \dfrac{h^2}{8m L^2}\]
For the Harmonic Oscillator with energies
\[E_v =\left ( v+\dfrac{1}{2} \right )h\nu\]
the zero-point energy (\(v=0\)) is
Many people have make cookie ideas of tapping into the zero-point energy to drive our economy. This is a silly idea and impossible, since this energy cannot be tapped (see https://van.physics.illinois.edu/qa/...ng.php?id=1256 for more discussion
Infrared Spectroscopy
Infrared (IR) spectroscopy is one of the most common and widely used spectroscopic techniques employed mainly by inorganic and organic chemists due to its usefulness in determining structures of compounds and identifying them. Chemical compounds have different chemical properties due to the presence of different functional groups. A molecule composed of n-atoms has 3n degrees of freedom, six of which are translations and rotations of the molecule itself. This leaves 3N-6 degrees of vibrational freedom (3N-5 if the molecule is linear). Vibrational modes are often given descriptive names, such as stretching, bending, scissoring, rocking and twisting. The four-atom molecule of formaldehyde, the gas phase spectrum of which is shown below, provides an example of these terms.
The spectrum of gas phase formaldehyde, is shown below.
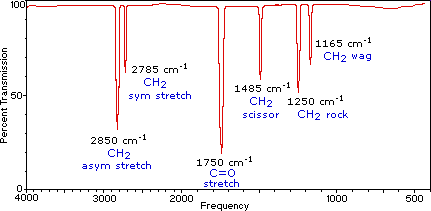
Gas Phase Infrared Spectrum of Formaldehyde, \(H_2C=O\)
Characteristic normal modes (vibrations) in formaldehyde
- \(CH_2\) Asymmetric Stretch
- \(CH_2\) Symmetric Stretch
- \(C=O\) Stretch
- \(CH_2\) Scissoring
- \(CH_2\) Rocking
- \(CH_2\) Wagging
The exact frequency at which a given vibration occurs is determined by the strengths of the bonds involved and the mass of the component atoms.
More on Dirac's Bra-Ket notation
In the early days of quantum theory, P. A. M. (Paul Adrian Maurice) Dirac created a powerful and concise formalism for it which is now referred to as Dirac notation or bra-ket (bracket \( \langle \, | \, \rangle\)) notation. Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics.
- kets: \(| \, \rangle\)
- bras: \(\langle \, | \)
- Bra-Ket Pairs (dot products): \(\langle Φ|Ψ \rangle\), consisting of a left part, \(\langle Φ|\), (the bra), and a right part, \(|Ψ\rangle\), (the ket).
For the ground state of the well-known particle-in-a-box with length \(L=1\).
\[\langle x | \psi \rangle = \psi(x) = 2^{1/2} \sin (\pi x) \]
However, if we wish to express \( \psi \) in momentum space we would write
\[ \langle p | \psi \rangle = \psi(p) = 2^{1/2} \dfrac{e^{-ip} +1}{\pi^2 - p^2} \]
How one finds this latter expression will be discussed later.
Spectroscopy is a matter-light interaction. You first need to know the results of the Schrödinger equation of a specific system. This includes both eigenstates (wavefuctions), eigenvalues (energies), and quantum numbers and You need to understand how to couple the eigenstates with electromagnetic radiation. This is done via the transition moment integral
\[\langle \psi_i | \hat{M}| \psi_f \rangle \label{26}\]
The transition moment integral gives information about the probability of a transition occurring. For IR of a single harmonic oscillator, \(\hat{M}\) can be set to \(x\). A more detailed discussion will be presented later. So the probability for a transition in HO is \[P_{i \rightarrow f} = \langle \psi_i | x | \psi_f \rangle\]
- From Equation \(\ref{26}\) comes general rules for absorption. For IR, the transition is allowed only if the molecule has a changing dipole moment.
- From Equation \(\ref{26}\) comes selection rules (what possible transitions are allowed). For IR this results in \(\Delta v = \pm 1\).
The vibration must change the molecular dipole moment to have a non-zero (electric) transition dipole moment. Molecules CAN have a zero net dipole moment, yet STILL UNDERGO transitions when stimulated by infrared light.
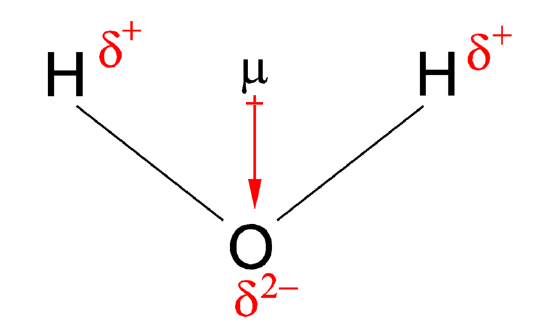
Dipole Moments (rehash from gen chem)
When two electrical charges, of opposite sign and equal magnitude, are separated by a distance, a dipole is established. The size of a dipole is measured by its dipole moment (\(\mu\)). Dipole moment is measured in Debye units, which is equal to the distance between the charges multiplied by the charge (1 Debye equals \(3.34 \times 10^{-30}\; C\, m\)). The dipole moment of a molecule can be calculated by Equation \(\ref{d1}\):
\[ \vec{\mu} = \sum_i q_i \, \vec{r}_i \label{d1}\]
where
- \(\vec{\mu}\) is the dipole moment vector
- \(q_i\) is the magnitude of the \(i^{th}\) charge, and
- \(\vec{r}_i\) is the vector representing the position of \(i^{th}\) charge.
The dipole moment acts in the direction of the vector quantity. An example of a polar molecule is \(\ce{H_2O}\). Because of the lone pair on oxygen, the structure of H2O is bent (predicted by the VSEPR model) that the vectors representing the dipole moment of each bond do not cancel each other out. Hence, water is polar.
Which molecules absorb IR radiation?
\(\ce{O2}\)
- Answer
-
No: Vibration does not change the dipole moment of the molecule due to symmetry.
\(\ce{HCl}\)
- Answer
-
Yes: Vibration does change the dipole moment of the molecule since there is a difference in electronegativity so the distance between the two atoms affects the dipole moment (Equation \ref{d1}).
\(\ce{H2}\)
- Answer
-
No: Vibration does not change the dipole moment of the molecule due to symmetry.
\(\ce{Cl2}\)
- Answer
-
No: Vibration does not change the dipole moment of the molecule due to symmetry.
\(\ce{CO2}\)
- Answer
-
Yes.: A vibration does change the dipole moment of the molecule since there is a difference in electronegativity so the distance between the two atoms affects the dipole moment. This is not the symmetric stretch, but the other modes.
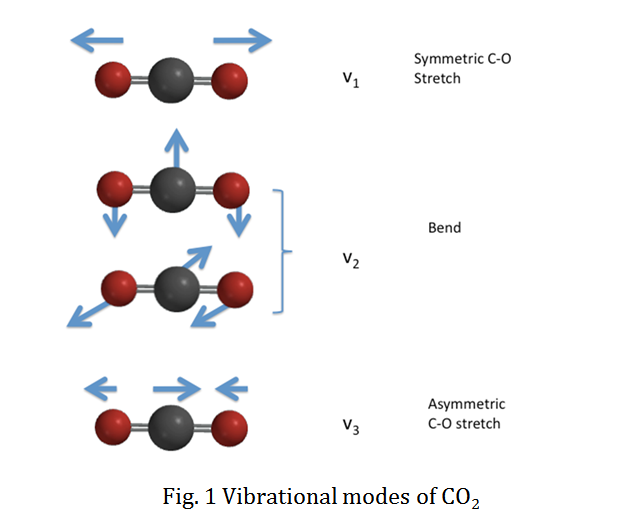
Energies of Harmonic Oscillators and IR Transitions
Using the harmonic oscillator and wave equations of quantum mechanics, the energy can be written in terms of the spring constant and reduced mass as
\[E = \left(v+\dfrac{1}{2}\right) \dfrac{h}{2\pi} \sqrt{\dfrac{k}{\mu}} \label{16}\]
where \(h\) is Planck's constant and \(v\) is the vibrational quantum number and ranges from 0,1,2,3.... infinity.
\[E = \left(v+\dfrac{1}{2}\right)h \nu_m \label{17}\]
where \(\nu\) is the vibrational frequency vibration. Transitions in vibrational energy levels can be brought about by absorption of radiation, provided the energy of the radiation exactly matches the difference in energy levels between the vibrational quantum states and provided the vibration causes a change in dipole moment. This can be expressed as
\[\Delta E = h\nu_m = \dfrac{h}{2\pi} \sqrt{\dfrac{k}{\mu}} \label{18}\]
At room temperature, the majority of molecules are in the ground state \(v = 0\), so the energies of these states are (via Equation \ref{18} with \(v=0\)):
\[E_o = \dfrac{1}{2}h \nu_m \label{19}\]
when a molecule absorbs energy, there is a promotion to a higher lying energy state. Let consider the first excited state with energy (via Equation \ref{18} with \(v=1\)):
\[ E_1 = \dfrac{3}{2} h\nu_m \label{20}\]
The energy associated with this transition is
\[\begin{align} \Delta E &= E_1 - E_0 \\[4pt] &= \dfrac{3}{2} h\nu_m - \dfrac{1}{2} h\nu_m \\[4pt] &= h\nu_m \label{21} \end{align}\]
The frequency of radiation \(\nu\) that will bring about this change is identical to the classical vibrational frequency (\(\nu_m\)) of the bond and it can be expressed as
\[ \begin{align} E_{radiation} = h\nu &= \Delta E \\[4pt] &= h\nu_m \\[4pt] &= \dfrac{h}{2\pi} \sqrt{\dfrac{k}{\mu}} \label{22} \end{align}\]
Equation \ref{22} can be expressed in wavenumbers (by dividing by \(c\)).
\[ \widetilde{\nu} = \dfrac{1}{2\pi c} \sqrt{\dfrac{k}{\mu}} \label{23}\]
where
- \(c\) is the velocity of light (cm s-1) and
- \(\widetilde{\nu}\) is the wave number of an absorption maximum (cm-1)
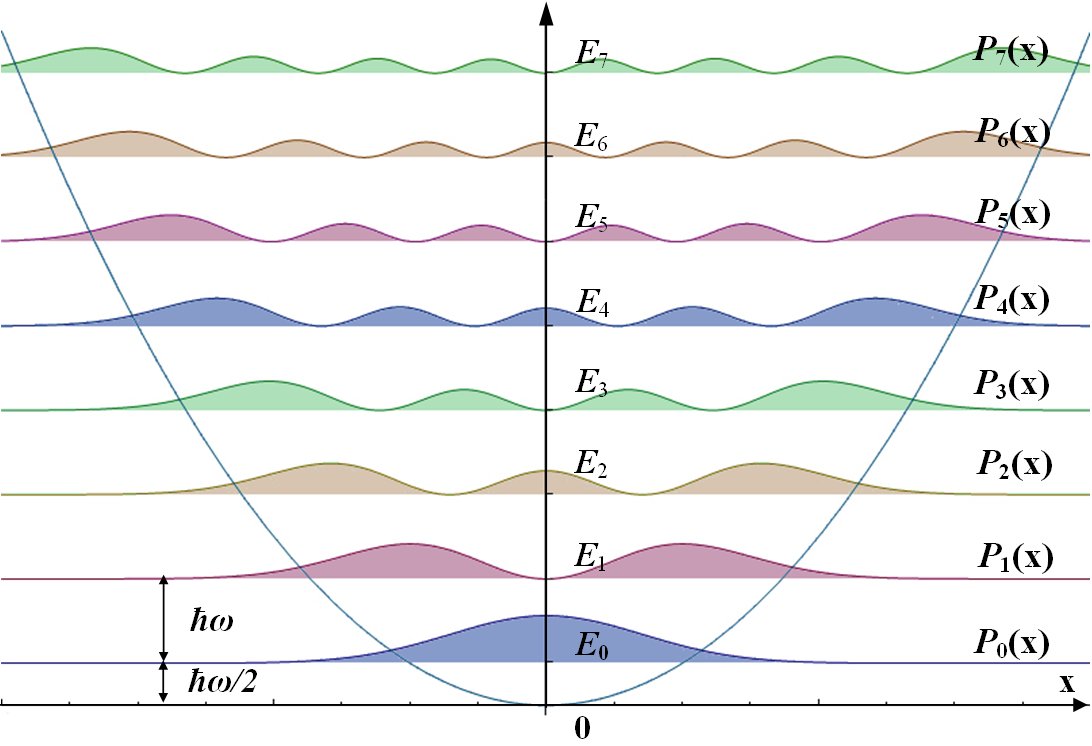
Corresponding probability densities. (Public domain; Allen McC.)
Java simulation of particles in boxes :https://phet.colorado.edu/en/simulation/bound-states

