4.4: Determining the Limiting Reactant
- Page ID
- 36992
- To understand the concept of limiting reactants and quantify incomplete reactions
In all the examples discussed thus far, the reactants were assumed to be present in stoichiometric quantities. Consequently, none of the reactants was left over at the end of the reaction. This is often desirable, as in the case of a space shuttle, where excess oxygen or hydrogen was not only extra freight to be hauled into orbit but also an explosion hazard. More often, however, reactants are present in mole ratios that are not the same as the ratio of the coefficients in the balanced chemical equation. As a result, one or more of them will not be used up completely but will be left over when the reaction is completed. In this situation, the amount of product that can be obtained is limited by the amount of only one of the reactants. The reactant that restricts the amount of product obtained is called the limiting reactant. The reactant that remains after a reaction has gone to completion is in excess.
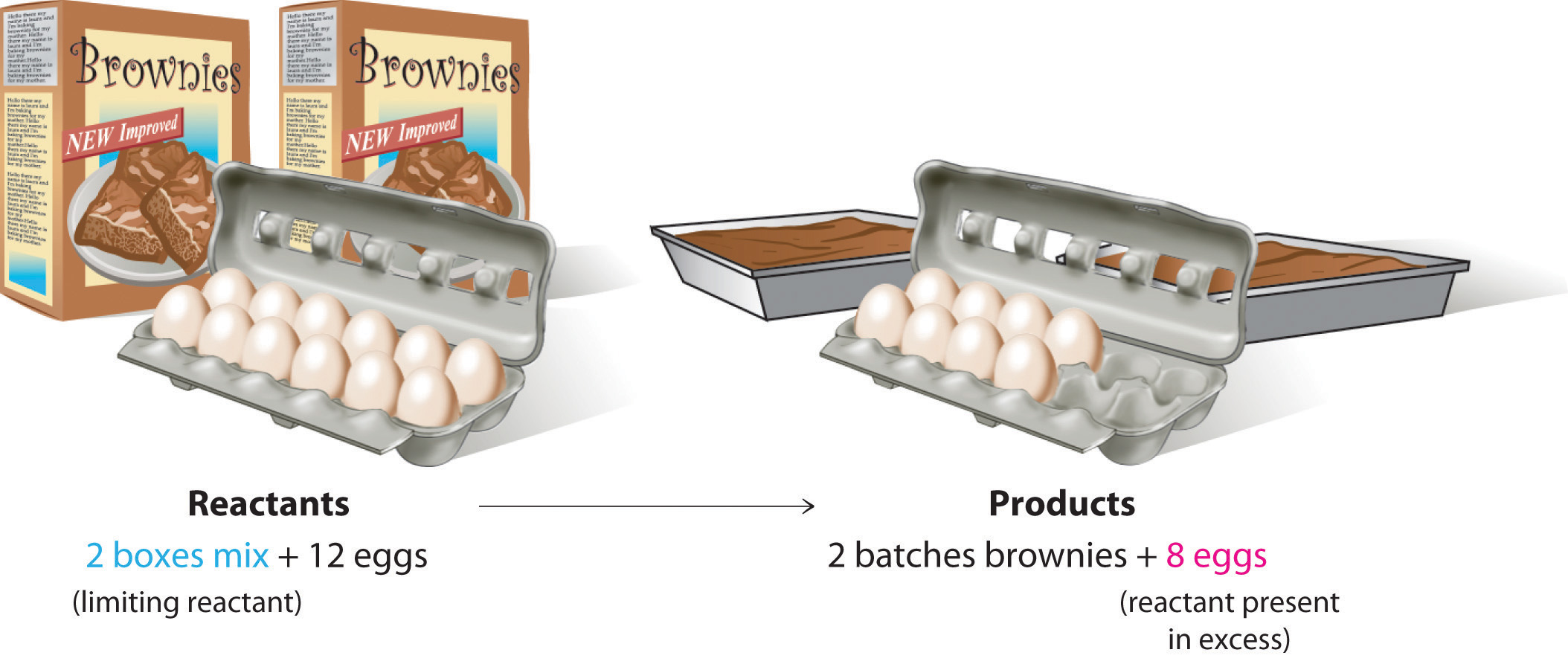
Consider a nonchemical example. Assume you have invited some friends for dinner and want to bake brownies for dessert. You find two boxes of brownie mix in your pantry and see that each package requires two eggs. The balanced equation for brownie preparation is thus
\[ 1 \,\text{box mix} + 2 \,\text{eggs} \rightarrow 1 \, \text{batch brownies} \label{4.4.1}\]
If you have a dozen eggs, which ingredient will determine the number of batches of brownies that you can prepare? Because each box of brownie mix requires two eggs and you have two boxes, you need four eggs. Twelve eggs is eight more eggs than you need. Although the ratio of eggs to boxes in is 2:1, the ratio in your possession is 6:1. Hence the eggs are the ingredient (reactant) present in excess, and the brownie mix is the limiting reactant. Even if you had a refrigerator full of eggs, you could make only two batches of brownies.
Now consider a chemical example of a limiting reactant: the production of pure titanium. This metal is fairly light (45% lighter than steel and only 60% heavier than aluminum) and has great mechanical strength (as strong as steel and twice as strong as aluminum). Because it is also highly resistant to corrosion and can withstand extreme temperatures, titanium has many applications in the aerospace industry. Titanium is also used in medical implants and portable computer housings because it is light and resistant to corrosion. Although titanium is the ninth most common element in Earth’s crust, it is relatively difficult to extract from its ores. In the first step of the extraction process, titanium-containing oxide minerals react with solid carbon and chlorine gas to form titanium tetrachloride (TiCl4) and carbon dioxide. Titanium tetrachloride is then converted to metallic titanium by reaction with magnesium metal at high temperature:
\[ TiCl_4 (g) + 2 \, Mg (l) \rightarrow Ti (s) + 2 \, MgCl_2 (l) \label{4.4.2}\]
Because titanium ores, carbon, and chlorine are all rather inexpensive, the high price of titanium (about $100 per kilogram) is largely due to the high cost of magnesium metal. Under these circumstances, magnesium metal is the limiting reactant in the production of metallic titanium.

With 1.00 kg of titanium tetrachloride and 200 g of magnesium metal, how much titanium metal can be produced according to the equation above? Solving this type of problem requires that you carry out the following steps:
- Determine the number of moles of each reactant.
- Compare the mole ratio of the reactants with the ratio in the balanced chemical equation to determine which reactant is limiting.
- Calculate the number of moles of product that can be obtained from the limiting reactant.
- Convert the number of moles of product to mass of product.
1. To determine the number of moles of reactants present, calculate or look up their molar masses: 189.679 g/mol for titanium tetrachloride and 24.305 g/mol for magnesium. The number of moles of each is calculated as follows:
\[ moles \, TiCl_4 = {mass \, TiCl_4 \over molar \, mass \, TiCl_4} \]
\[ = 1000 \, g \, TiCl_4 \times {1 \, mol \, TiCl_4 \over 189.679 \, g \, TiCl_4} = 5.272 \, mol \, TiCl_4 \]
\[ moles \, Mg = {mass \, Mg \over molar \, mass \, Mg}\]
\[ = 200 \, g \, Mg \times {1 \, mol \, Mg \over 24.305 \, g \, Mg } = 8.23 \, mol \, Mg \]
2. There are more moles of magnesium than of titanium tetrachloride, but the ratio is only the following:
\[ {mol \, Mg \over mol \, TiCl_4} = {8.23 \, mol \over 5.272 \, mol } = 1.56 \]
Because the ratio of the coefficients in the balanced chemical equation is,
\[{ 2 \, mol \, Mg \over 1 \, mol \, TiCl_4} = 2 \]
there is not have enough magnesium to react with all the titanium tetrachloride. If this point is not clear from the mole ratio, calculate the number of moles of one reactant that is required for complete reaction of the other reactant. For example, there are 8.23 mol of Mg, so (8.23 ÷ 2) = 4.12 mol of TiCl4 are required for complete reaction. Because there are 5.272 mol of TiCl4, titanium tetrachloride is present in excess. Conversely, 5.272 mol of TiCl4 requires 2 × 5.272 = 10.54 mol of Mg, but there are only 8.23 mol. Therefore, magnesium is the limiting reactant.
3. Because magnesium is the limiting reactant, the number of moles of magnesium determines the number of moles of titanium that can be formed:
\[ moles \, Ti = 8.23 \, mol \, Mg = {1 \, mol \, Ti \over 2 \, mol \, Mg} = 4.12 \, mol \, Ti \]
Thus only 4.12 mol of Ti can be formed.
4. To calculate the mass of titanium metal that can obtain, multiply the number of moles of titanium by the molar mass of titanium (47.867 g/mol):
\[ moles \, Ti = mass \, Ti \times molar \, mass \, Ti = 4.12 \, mol \, Ti \times {47.867 \, g \, Ti \over 1 \, mol \, Ti} = 197 \, g \, Ti \]
Here is a simple and reliable way to identify the limiting reactant in any problem of this sort:
- Calculate the number of moles of each reactant present: 5.272 mol of TiCl4 and 8.23 mol of Mg.
- Divide the actual number of moles of each reactant by its stoichiometric coefficient in the balanced chemical equation: \[ TiCl_4 : { 5.272 \, mol \, (actual) \over 1 \, mol \, (stoich)} = 5.272 \, \, \, \, Mg: {8.23 \, mol \, (actual) \over 2 \, mol \, (stoich)} = 4.12 \]
- The reactant with the smallest mole ratio is limiting. Magnesium, with a calculated stoichiometric mole ratio of 4.12, is the limiting reactant.
Density is the mass per unit volume of a substance. If we are given the density of a substance, we can use it in stoichiometric calculations involving liquid reactants and/or products, as Example \(\PageIndex{1}\) demonstrates.
Determining the Limiting Reactant and Theoretical Yield for a Reaction: https://youtu.be/HmDm1qpNUD0
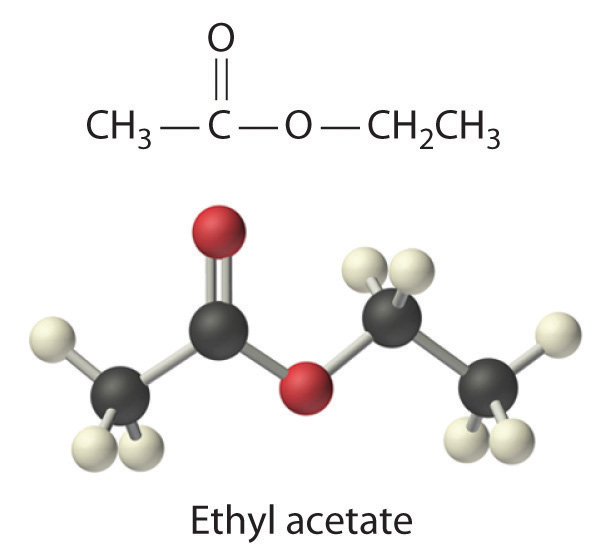
Ethyl acetate (CH3CO2C2H5) is the solvent in many fingernail polish removers and is used to decaffeinate coffee beans and tea leaves. It is prepared by reacting ethanol (C2H5OH) with acetic acid (CH3CO2H); the other product is water. A small amount of sulfuric acid is used to accelerate the reaction, but the sulfuric acid is not consumed and does not appear in the balanced chemical equation. Given 10.0 mL each of acetic acid and ethanol, how many grams of ethyl acetate can be prepared from this reaction? The densities of acetic acid and ethanol are 1.0492 g/mL and 0.7893 g/mL, respectively.
Given: reactants, products, and volumes and densities of reactants
Asked for: mass of product
Strategy:
- Balance the chemical equation for the reaction.
- Use the given densities to convert from volume to mass. Then use each molar mass to convert from mass to moles.
- Using mole ratios, determine which substance is the limiting reactant. After identifying the limiting reactant, use mole ratios based on the number of moles of limiting reactant to determine the number of moles of product.
- Convert from moles of product to mass of product.
Solution:
A Always begin by writing the balanced chemical equation for the reaction:
\[ C_2H_5OH (l) + CH_3CO_2H (aq) \rightarrow CH_3CO_2C_2H_5 (aq) + H_2O (l) \]
B We need to calculate the number of moles of ethanol and acetic acid that are present in 10.0 mL of each. Recall from that the density of a substance is the mass divided by the volume:
\[ density = {mass \over volume } \]
Rearranging this expression gives mass = (density)(volume). We can replace mass by the product of the density and the volume to calculate the number of moles of each substance in 10.0 mL (remember, 1 mL = 1 cm3):
\[ moles \, C_2H_5OH = { mass \, C_2H_5OH \over molar \, mass \, C_2H_5OH } \]
\[ = {volume \, C_2H_5OH \times density \, C_2H_5OH \over molar \, mass \, C_2H_5OH}\]
\[ = 10.0 \, ml \, C_2H_5OH \times {0.7893 \, g \, C_2H_5OH \over 1 \, ml \, C_2H_5OH} \times {1 \, mole \, C_2H_5OH \over 46.07 \, g\, C_2H_5OH}\]
\[ = 0.171 \, mol \, C_2H_5OH \]
\[moles \, CH_3CO_2H = {mass \, CH_3CO_2H \over molar \, mass \, CH_3CO_2H} \]
\[= {volume \, CH_3CO_2H \times density \, CH_3CO_2H \over molar \, mass \, CH_3CO_2H} \]
\[= 10.0 \, ml \, CH_3CO_2H \times {1.0492 \, g \, CH_3CO_2H \over 1 \, ml \, CH_3CO_2H} \times {1 \, mol \, CH_3CO_2H \over 60.05 \, g \, CH_3CO_2H } \]
\[= 0.175 \, mol \, CH_3CO_2H \]
C The number of moles of acetic acid exceeds the number of moles of ethanol. Because the reactants both have coefficients of 1 in the balanced chemical equation, the mole ratio is 1:1. We have 0.171 mol of ethanol and 0.175 mol of acetic acid, so ethanol is the limiting reactant and acetic acid is in excess. The coefficient in the balanced chemical equation for the product (ethyl acetate) is also 1, so the mole ratio of ethanol and ethyl acetate is also 1:1. This means that given 0.171 mol of ethanol, the amount of ethyl acetate produced must also be 0.171 mol:
\[ moles \, ethyl \, acetate = molethanol \times {1 \, mol \, ethyl \, acetate \over 1 \, mol \, ethanol } \]
\[ = 0.171 \, mol \, C_2H_5OH \times {1 \, mol \, CH_3CO_2C_2H_5 \over 1 \, mol \, C_2H_5OH} \]
\[ = 0.171 \, mol \, CH_3CO_2C_2H_5 \]
D The final step is to determine the mass of ethyl acetate that can be formed, which we do by multiplying the number of moles by the molar mass:
\[mass \, of \, ethyl \, acetate = moleethyl \, acetate \times molar \, mass \, ethyl \, acetate\]
\[ = 0.171 \, mol \, CH_3CO_2C_2H_5 \times {88.11 \, g \, CH_3CO_2C_2H_5 \over 1 \, mol \, CH_3CO_2C_2H_5}\]
\[ = 15.1 \, g \, CH_3CO_2C_2H_5 \]
Thus 15.1 g of ethyl acetate can be prepared in this reaction. If necessary, you could use the density of ethyl acetate (0.9003 g/cm3) to determine the volume of ethyl acetate that could be produced:
\[ volume \, of \, ethyl \, acetate = 15.1 \, g \, CH_3CO_2C_2H_5 \times { 1 \, ml \, CH_3CO_2C_2H_5 \over 0.9003 \, g\, CH_3CO_2C_2H_5} \]
\[ = 16.8 \, ml \, CH_3CO_2C_2H_5 \]
Under appropriate conditions, the reaction of elemental phosphorus and elemental sulfur produces the compound P4S10. How much P4S10 can be prepared starting with 10.0 g of P4 and 30.0 g of S8?
Answer: 35.9 g
Limiting Reactants in Solutions
The concept of limiting reactants applies to reactions carried out in solution as well as to reactions involving pure substances. If all the reactants but one are present in excess, then the amount of the limiting reactant may be calculated as illustrated in Example \(\PageIndex{2}\).
Because the consumption of alcoholic beverages adversely affects the performance of tasks that require skill and judgment, in most countries it is illegal to drive while under the influence of alcohol. In almost all US states, a blood alcohol level of 0.08% by volume is considered legally drunk. Higher levels cause acute intoxication (0.20%), unconsciousness (about 0.30%), and even death (about 0.50%). The Breathalyzer is a portable device that measures the ethanol concentration in a person’s breath, which is directly proportional to the blood alcohol level. The reaction used in the Breathalyzer is the oxidation of ethanol by the dichromate ion:
\[ 3CH_3 CH_2 OH(aq) + \underset{yellow-orange}{2Cr_2 O_7^{2 -}}(aq) + 16H ^+ (aq) \underset{H_2 SO_4 (aq)}{\xrightarrow{\hspace{10px} Ag ^+\hspace{10px}} } 3CH_3 CO_2 H(aq) + \underset{green}{4Cr^{3+}} (aq) + 11H_2 O(l) \]
When a measured volume (52.5 mL) of a suspect’s breath is bubbled through a solution of excess potassium dichromate in dilute sulfuric acid, the ethanol is rapidly absorbed and oxidized to acetic acid by the dichromate ions. In the process, the chromium atoms in some of the Cr2O72− ions are reduced from Cr6+ to Cr3+. In the presence of Ag+ ions that act as a catalyst, the reaction is complete in less than a minute. Because the Cr2O72− ion (the reactant) is yellow-orange and the Cr3+ ion (the product) forms a green solution, the amount of ethanol in the person’s breath (the limiting reactant) can be determined quite accurately by comparing the color of the final solution with the colors of standard solutions prepared with known amounts of ethanol.

A Breathalyzer reaction with a test tube before (a) and after (b) ethanol is added. When a measured volume of a suspect’s breath is bubbled through the solution, the ethanol is oxidized to acetic acid, and the solution changes color from yellow-orange to green. The intensity of the green color indicates the amount of ethanol in the sample.
A typical Breathalyzer ampul contains 3.0 mL of a 0.25 mg/mL solution of K2Cr2O7 in 50% H2SO4 as well as a fixed concentration of AgNO3 (typically 0.25 mg/mL is used for this purpose). How many grams of ethanol must be present in 52.5 mL of a person’s breath to convert all the Cr6+ to Cr3+?
Given: volume and concentration of one reactant
Asked for: mass of other reactant needed for complete reaction
Strategy:
- Calculate the number of moles of Cr2O72− ion in 1 mL of the Breathalyzer solution by dividing the mass of K2Cr2O7 by its molar mass.
- Find the total number of moles of Cr2O72− ion in the Breathalyzer ampul by multiplying the number of moles contained in 1 mL by the total volume of the Breathalyzer solution (3.0 mL).
- Use the mole ratios from the balanced chemical equation to calculate the number of moles of C2H5OH needed to react completely with the number of moles of Cr2O72− ions present. Then find the mass of C2H5OH needed by multiplying the number of moles of C2H5OH by its molar mass.
Solution:
A In any stoichiometry problem, the first step is always to calculate the number of moles of each reactant present. In this case, we are given the mass of K2Cr2O7 in 1 mL of solution, which can be used to calculate the number of moles of K2Cr2O7 contained in 1 mL:
\( \dfrac{moles\: K_2 Cr_2 O_7} {1\: mL} = \dfrac{(0 .25\: \cancel{mg}\: K_2 Cr_2 O_7 )} {mL} \left( \dfrac{1\: \cancel{g}} {1000\: \cancel{mg}} \right) \left( \dfrac{1\: mol} {294 .18\: \cancel{g}\: K_2 Cr_2 O_7} \right) = 8.5 \times 10 ^{-7}\: moles \)
B Because 1 mol of K2Cr2O7 produces 1 mol of Cr2O72− when it dissolves, each milliliter of solution contains 8.5 × 10−7 mol of Cr2O72−. The total number of moles of Cr2O72− in a 3.0 mL Breathalyzer ampul is thus
\( moles\: Cr_2 O_7^{2-} = \left( \dfrac{8 .5 \times 10^{-7}\: mol} {1\: \cancel{mL}} \right) ( 3 .0\: \cancel{mL} ) = 2 .6 \times 10^{-6}\: mol\: Cr_2 O_7^{2–} \)
C The balanced chemical equation tells us that 3 mol of C2H5OH is needed to consume 2 mol of Cr2O72− ion, so the total number of moles of C2H5OH required for complete reaction is
\( moles\: of\: C_2 H_5 OH = ( 2.6 \times 10 ^{-6}\: \cancel{mol\: Cr_2 O_7 ^{2-}} ) \left( \dfrac{3\: mol\: C_2 H_5 OH} {2\: \cancel{mol\: Cr _2 O _7 ^{2 -}}} \right) = 3 .9 \times 10 ^{-6}\: mol\: C _2 H _5 OH \)
As indicated in the strategy, this number can be converted to the mass of C2H5OH using its molar mass:
\( mass\: C _2 H _5 OH = ( 3 .9 \times 10 ^{-6}\: \cancel{mol\: C _2 H _5 OH} ) \left( \dfrac{46 .07\: g} {\cancel{mol\: C _2 H _5 OH}} \right) = 1 .8 \times 10 ^{-4}\: g\: C _2 H _5 OH \)
Thus 1.8 × 10−4 g or 0.18 mg of C2H5OH must be present. Experimentally, it is found that this value corresponds to a blood alcohol level of 0.7%, which is usually fatal.
The compound para-nitrophenol (molar mass = 139 g/mol) reacts with sodium hydroxide in aqueous solution to generate a yellow anion via the reaction
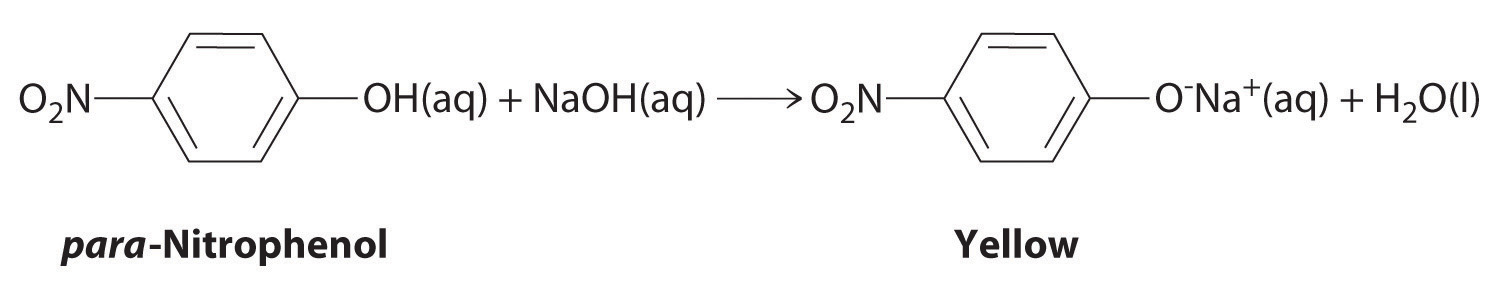
Because the amount of para-nitrophenol is easily estimated from the intensity of the yellow color that results when excess NaOH is added, reactions that produce para-nitrophenol are commonly used to measure the activity of enzymes, the catalysts in biological systems. What volume of 0.105 M NaOH must be added to 50.0 mL of a solution containing 7.20 × 10−4 g of para-nitrophenol to ensure that formation of the yellow anion is complete?
Answer: 4.93 × 10−5 L or 49.3 μL
In Examples 4.4.1 and 4.4.2, the identities of the limiting reactants are apparent: [Au(CN)2]−, LaCl3, ethanol, and para-nitrophenol. When the limiting reactant is not apparent, it can be determined by comparing the molar amounts of the reactants with their coefficients in the balanced chemical equation. The only difference is that the volumes and concentrations of solutions of reactants, rather than the masses of reactants, are used to calculate the number of moles of reactants, as illustrated in Example \(\PageIndex{3}\).
When aqueous solutions of silver nitrate and potassium dichromate are mixed, an exchange reaction occurs, and silver dichromate is obtained as a red solid. The overall chemical equation for the reaction is as follows:
\(2AgNO_3(aq) + K_2Cr_2O_7(aq) \rightarrow Ag_2Cr_2O_7(s) + 2KNO_3(aq) \)
What mass of Ag2Cr2O7 is formed when 500 mL of 0.17 M K2Cr2O7 are mixed with 250 mL of 0.57 M AgNO3?
Given: balanced chemical equation and volume and concentration of each reactant
Asked for: mass of product
Strategy:
- Calculate the number of moles of each reactant by multiplying the volume of each solution by its molarity.
- Determine which reactant is limiting by dividing the number of moles of each reactant by its stoichiometric coefficient in the balanced chemical equation.
- Use mole ratios to calculate the number of moles of product that can be formed from the limiting reactant. Multiply the number of moles of the product by its molar mass to obtain the corresponding mass of product.
Solution:
A The balanced chemical equation tells us that 2 mol of AgNO3(aq) reacts with 1 mol of K2Cr2O7(aq) to form 1 mol of Ag2Cr2O7(s) (Figure \(\PageIndex{2}\)). The first step is to calculate the number of moles of each reactant in the specified volumes:
\[ moles\: K_2 Cr_2 O_7 = 500\: \cancel{mL} \left( \dfrac{1\: \cancel{L}} {1000\: \cancel{mL}} \right) \left( \dfrac{0 .17\: mol\: K_2 Cr_2 O_7} {1\: \cancel{L}} \right) = 0 .085\: mol\: K_2 Cr_2 O_7 \]
\[ moles\: AgNO_3 = 250\: \cancel{mL} \left( \dfrac{1\: \cancel{L}} {1000\: \cancel{mL}} \right) \left( \dfrac{0 .57\: mol\: AgNO_3} {1\: \cancel{L}} \right) = 0 .14\: mol\: AgNO_3 \]
B Now determine which reactant is limiting by dividing the number of moles of each reactant by its stoichiometric coefficient:
\[K_2 Cr_2 O_7: \: \dfrac{0 .085\: mol} {1\: mol} = 0 .085 \]
\[ AgNO_3: \: \dfrac{0 .14\: mol} {2\: mol} = 0 .070 \]
Because 0.070 < 0.085, we know that AgNO3 is the limiting reactant.
C Each mole of Ag2Cr2O7 formed requires 2 mol of the limiting reactant (AgNO3), so we can obtain only 0.14/2 = 0.070 mol of Ag2Cr2O7. Finally, convert the number of moles of Ag2Cr2O7 to the corresponding mass:
\[ mass\: of\: Ag_2 Cr_2 O_7 = 0 .070\: \cancel{mol} \left( \dfrac{431 .72\: g} {1 \: \cancel{mol}} \right) = 30\: g \: Ag_2 Cr_2 O_7 \]
The Ag+ and Cr2O72− ions form a red precipitate of solid Ag2Cr2O7, while the K+ and NO3− ions remain in solution. (Water molecules are omitted from molecular views of the solutions for clarity.)
Aqueous solutions of sodium bicarbonate and sulfuric acid react to produce carbon dioxide according to the following equation:
\(2NaHCO_3(aq) + H_2SO_4(aq) \rightarrow 2CO_2(g) + Na_2SO_4(aq) + 2H_2O(l)\)
If 13.0 mL of 3.0 M H2SO4 are added to 732 mL of 0.112 M NaHCO3, what mass of CO2 is produced?
Answer: 3.4 g
Limiting Reactant Problems Using Molarities: https://youtu.be/eOXTliL-gNw
Summary
- The stoichiometry of a balanced chemical equation identifies the maximum amount of product that can be obtained.
The stoichiometry of a reaction describes the relative amounts of reactants and products in a balanced chemical equation. A stoichiometric quantity of a reactant is the amount necessary to react completely with the other reactant(s). If a quantity of a reactant remains unconsumed after complete reaction has occurred, it is in excess. The reactant that is consumed first and limits the amount of product(s) that can be obtained is the limiting reactant. To identify the limiting reactant, calculate the number of moles of each reactant present and compare this ratio to the mole ratio of the reactants in the balanced chemical equation. The maximum amount of product(s) that can be obtained in a reaction from a given amount of reactant(s) is the theoretical yield of the reaction. The actual yield is the amount of product(s) actually obtained in the reaction; it cannot exceed the theoretical yield. The percent yield of a reaction is the ratio of the actual yield to the theoretical yield, expressed as a percentage.
Contributors and Attributions
Modified by Joshua Halpern (Howard University)

