5.E: Chemical Equilibrium (Exercises)
- Page ID
- 69601
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)These are homework exercises to accompany the Textmap created for "Principles of Modern Chemistry" by Oxtoby et al. Complementary General Chemistry question banks can be found for other Textmaps and can be accessed here.
Q1
Write an expression for the equilibrium constant \(K_c\) for each reaction below.
- \(\ce{2 NO(g) + O2(g) <=> 2 NO2(g)}\)
- \(\ce{N2H4(g) + 3 O2(g) <=> 2 NO2(g) + H2O(g)}\)
- \(\ce{O3(g) + H2O(l) <=> H2(g) + 2 O2(g)}\)
- Solution
-
For a general reaction \(\ce{aA + bB <=> cC + dD}\) then Law of Mass Action argues we can construct an equilibrium constant thusly
\[ K_c = \ce{\dfrac{[C]^c[D]^d}{[A]^a[B]^b}} \nonumber \]
This is the general equations to substitute the reactants and product concentrations (with coefficients as exponents).
\[ K_c = \ce{\dfrac{[C]^{c} [D]^{d}}{[A]^{a} [B]^{b}}} \nonumber \]
- \( K_c = \ce{\dfrac{[NO2]^2}{[NO]^2 [O2]}} \)
- \( K_c = \ce{\dfrac{[H2O][NO2]^2}{[N2H4] [O2]^3}} \)
- \( K_c = \ce{\dfrac{[O2]^2 [H2]}{[O3]}} \)
Note that for part c, \(\ce{H2O (l)}\) is not included because pure solids and liquids are not included in the equilibrium constant.
Q3
Gaseous chlorine reacts with water vapor to form hydrogen chloride and oxygen gas. Write down the equilibrium expression (\(K_p\)) for the reaction.
- Solution
-
First, a balanced reaction is constructed to ensure the equilibrium expression will be correctly states.
\[\ce{2Cl_2 + 2H_2O <=> 4HCl + O2} \nonumber \]
Equilibrium expression \(K_p\) is as follows:
\[ K_p = \dfrac{p^4_{\ce{HCl}} p_{\ce{O2}}}{p^2_{\ce{Cl2}}p^2_{\ce{H2O}}}\nonumber \]
Q11
For each thermodynamics equilibrium expressions outlined below, determine one possible chemical reaction related to each.
- \[K=\frac{a\{\ce{CO}\}^{2}}{a\{\ce{CO_{2}}\}}\nonumber \]
- \[K=\frac{a\{\ce{H_{2}O}\}^{2}}{a\{\ce{H_{2}}\}^{2} a\{\ce{O_{2} }\} }\nonumber \]
- \[K=\frac{a\{\ce{Cl_{2}O}\}^{2}}{a\{\ce{Cl_{2}}\}^{2} a\{\ce{O_{2}}\} }\nonumber \]
- \[K=\frac{a\{\ce{COCl_{2}}\}}{a\{\ce{CO}\}\cdot a\{\ce{Cl_{2}}\}}\nonumber \]
- Solution
-
- \[\ce{CO2(g) + C(s) <=> 2 CO(g)}\nonumber \]
- \[\ce{2 H2(g) + O2(g) <=> 2 H2O(g)}\nonumber \]
- \[\ce{2 Cl2(g) + O2(g) <=> 2 Cl2O(g)}\nonumber \]
- \[\ce{CO(g) + Cl2(g) <=> COCl2(g)}\nonumber \]
Q15A
Based on the following data, calculate the equilibrium constant and the value of ΔG at 273 K.
a. \(\ce{CO2(g) + H2(g) <=> CO(g) + H2O(g)} \) with
- \([\ce{CO2}]_{\text{eq}} = 0.0954 \,\text{M} \)
- \([\ce{H2}]_{\text{eq}} = 0.0454 \,\text{M}\)
- \([\ce{CO}]_{\text{eq}} = 0.0046 \,\text{M} \)
- \([\ce{H2O}]_{\text{eq}} = 0.0046 \,\text{M} \)
b. \(\ce{2NO(g) + 2H2(g) <=> N2(g) + 2H2O(g)} \) with
- \([\ce{NO}]_{\text{eq}} = 0.45\, \text{M} \)
- \([\ce{H2}]_{\text{eq}} = 0.63 \,\text{M}\)
- \([\ce{N2}]_{\text{eq}} = 0.95 \,\text{M} \)
- \([\ce{H2O}]_{\text{eq}} = 1.3 \, \text{M} \)
- Solution
-
a) \[\begin{align*} K &= \dfrac{\ce{[CO]}\ce{[H2O]}}{\ce{[CO2]}\ce{[H2]}} \\[4pt] &= \dfrac{(0.0046)(0.0046)}{(0.0954)(0.0454)} \\[4pt] &= 4.9 \times 10^{-3} \end{align*}\]
\[\Delta G = R T \ln(K) = (8.3145 \, \text{J/(K mol)})(273 \, \text{K}) \ln(4.9 \times 10^{-3}) = -12072.288 \, \text{J/mol} \nonumber\]
b) \[K = \ce{\frac{[N2][H2O]^2}{[NO]^2[H2]^2}} = \frac{[0.95][1.3]^2}{[0.45]^2[0.63]^2} = 19.98 \nonumber \]
\[\Delta G = R T \ln(K) = (8.3145 \, \text{J/K mol})(273 \, \text{K}) \ln(19.98) = 6797.62 \, \text{J/mol} \nonumber \]
Q15B
Calculate the appropriate K value for the following reactions using the information provided. Assume that they are preformed under standard conditions (and 298.15 K).
- \[\ce{2 NO2(g) <=> 2 NO(g) + O2(g) }\nonumber \]
- \[\ce{NH4+ (aq) + H2O(l) <=> H3O+ (aq) + NH3 (aq)}\nonumber \]
- Jim’s brother, Txeltoqlztop, goes to the bathroom only to find out that his sibling did not refill the toilet paper roll! To get revenge, Txeltoqlztop decides to fill his brother’s room with carbon monoxide, via the following reaction: \[\ce{2 CH4 (g) + 3 O2 (g) <=> 2 CO(g) + 4 H2O(g)} \nonumber \] Calculate the K value for this equation under standard conditions, interpret what it means in regards to the direction this equation will go, and compare it to the other two.
- Solution
-
The core of this problem is to find the K value and understanding what information it can describe about the reaction. Since the problem provides many, many \(\Delta{G_{f}}\), it is likely that to calculate the K value, a relationship needs to be drawn from \(\Delta{G}\) to K. This relationship is as follows:
\[\Delta{G_{\text{rxn}}^{\circ}}= -RT \ln\left(K_{p}\right)\nonumber \]
Relevant Information obtained from the thermodynamic tables
\(\Delta{G_f^{\circ}}\; \ce{NO2(g)} = 51.30 \mathrm{\dfrac{kJ}{mol}}\) \(\Delta{G_f^{\circ}}\; \ce{H3O^+(aq)} = -103.45 \mathrm{\dfrac{kJ}{mol}}\)
\(\Delta{G_f^{\circ}}\; \ce{NO(g)} = 86.57 \mathrm{\dfrac{kJ}{mol}}\) \(\Delta{G_f^{\circ}}\; \ce{NH3(aq)} = -26.5 \mathrm{\dfrac{kJ}{mol}}\)
\(\Delta{G_f^{\circ}}\; \ce{O2(g)} = 0 \mathrm{\dfrac{kJ}{mol}}\) \(\Delta{G_f^{\circ}}\; \ce{CH4(g)} = -50.84 \mathrm{\dfrac{kJ}{mol}}\)
\(\Delta{G_f^{\circ}}\; \ce{NH4^+ (aq)} = -79.37 \mathrm{\dfrac{kJ}{mol}}\) \(\Delta{G_f^{\circ}}\; \ce{CO(g)} = -137.28 \mathrm{\dfrac{kJ}{mol}}\)
\(\Delta{G_f^{\circ}}\; \ce{H2O(l)} = -237.14 \mathrm{\dfrac{kJ}{mol}}\) \(\Delta{G_f^{\circ}}\; \ce{H2O(g)} = -228.61 \mathrm{\dfrac{kJ}{mol}}\)
Note that the relationship here is between \(\Delta{G}\) and \(K_p\), which is:
\[K_p \approx \dfrac{P_{\text{products}}}{P_{\text{reactants}}} \nonumber \]
Where \(P\) is partial pressure of the products or reactants. The reason this is an approximation is because the equilibrium actually measures the activities of the species, but by using just the partial pressures a good estimate is procured. Since the equation relating \(K_p\) and \(\Delta{G}\) only has these two variables as unknown, once \(\Delta{G}\) is found, algebra can find \(K_p\). The process for utilizing Hess's Law to find state variables is outlined extensively. The values below were found using the exact same process, now for \(\Delta{G}\) (Just in case, the Hess law formula is provided).
\(\Delta{G^{\circ}} = \sum{n_{\text{products}} \times {\Delta{G_{f_{\text{products}}}^{\circ}}}} - \sum{n_{\text{reactants}}\times{\Delta{G_{f_{\text{reactants}}}^{\circ}}}}\)
\(\Delta G^{\circ} (\ce{2 NO2(g)<=> 2 NO(g) + O2 (g)}) = 70.42 \, \mathrm{\dfrac{kJ}{mol}}\)
\(\Delta G^{\circ} (\ce{NH4^+ (aq) + H2O(l) <=> H3O^+(aq) + NH3 (aq)}) = -437.93 \mathrm{\dfrac{kJ}{mol}}\)
\(\Delta G^{\circ} (\ce{2 CH4 (g) + 3 O2 (g) <=> 2 CO(g) + 4 H2O (l)}) = -1121.44 \mathrm{\dfrac{kJ}{mol}}\)
To find K, plug in the \(\Delta{G}\) into the equation above. (Note that the solution does NOT show the conversion of the gas constant from J to kJ!!)
\(\Delta{G_{\text{rxn}}^{\circ}}= -\left(8.314 \, \mathrm{\dfrac{J}{mol \, K}} \right)\left(298.15 \, \mathrm{K}\right)\times{\ln\left(K_{p}\right)}\)
\(70.54 \mathrm{\dfrac{kJ}{mol}} = -\left(8.314 \mathrm{\dfrac{J}{mol \, K}}\right)\left(298.15 \, \mathrm{K}\right)\times{\ln\left(K_{p}\right)}\)
\(-\dfrac{70.54 \mathrm{\dfrac{kJ}{mol}}}{\left(8.314 \mathrm{\dfrac{J}{molK}}\right)\left(298.15 \, \mathrm{K}\right)}= \ln\left(K_{p}\right)\)
\(e^{-\dfrac{70.54 \mathrm{\dfrac{kJ}{mol}}}{\left(8.314 \mathrm{\dfrac{J}{mol \, K}}\right)\left(298.15 \, \mathrm{K}\right)}} = K_{p}\)
\(K_{p} \approx e^{-28.457} \approx 4.3776\times10^{-13}\)
Thus, the \(K_{p}\) value for \(\ce{2 NO2 (g) <=> 2 NO (g) + O2 (g)}\) is a very small number!. Since the equilibrium value depicts the ratio of products to reactants at the equilibrium point, this very tiny \(K_{p}\) value means that the reaction will heavily favor the reactants. The third reaction where Txeltoqlztop wants to poison his brother with \(\ce{CO}\) also follows the same process, and the answer is such:
\(K_{p} \approx e^{452}\)
\(e^{452}\) is a really big number! That means, while the previous reaction will stay mostly on the reactant sides, this reaction heavily favors the products side, meaning that pretty much all of the methane and oxygen that Txeltoqlztop uses will be transformed into carbon monoxide, which is all the better for him!
The same method can be applied to the aqueous reaction, but the \(K\) value calculated is \(K_{c}\) rather than \(K_{p}\).
\(K_{c} \approx e^{-176.65} \approx 1.898 \times 10^{-77}\)*
*These equilibrium constants are based solely off the calculated Gibbs energy, some of the reactions, therefore, may have actual K values much different from the ones calculated.
Abstract: use of \(\Delta G_{\text{rxn}}^{\circ} = -RT \times \ln\left(K_p\right)\)
Q15C
Use the thermodynamic data in Tables T1 and T2 to calculate the equilibrium constants for the following equations at 25°C.
- \(\ce{H2(g) + 2F(g) <=> 2HF(g)}\)
- \(\ce{FeCl3(s) <=> FeCl2(s) + Cl2(g)}\)
- \(\ce{CaSO4(s) <=> Ca^{2+}(aq) + SO4^{2-} (aq)}\)
- Solution
-
For each of the chemical reactions, the main equation needed is
\[ \Delta G_{\text{rxn}} = -R \times T \times \ln K \nonumber \]
Where R is 8.134 J K-1 mol-1 and T is equal to 298K. In order to determine the value of Grxn, the following the reaction is needed
\[ \Delta G_{\text{rxn}} = \sum n G_{f}^{\circ} (\text{products}) - \sum n G_{f}^{\circ} (\text{reactants}) \nonumber \]
a. By looking in the tables, the \( \Delta G\) of formation can be found and they are listed for each compound below
H2(g) = 203.3 J mol-1, F2(g) = 62.3 J mol-1, HF(g)=-275.4 J mol-1
Next, these values are plugged into the second equation to the the change in Gibbs energy for the reaction
\[ \Delta G_{\text{rxn}} = -275.4\; \mathrm{J \, mol^{-1}} - (203.3\; \mathrm{J \, mol^{-1}} + 62.3\; \mathrm{J \, mol^{-1}}) = -514\; \mathrm{J \, mol^{-1}} \nonumber \]
Using the the value for the Gibbs Energy, the value of K can be determined using the first equation
\[ -541\; \mathrm{J \, mol^{-1}} = -8.314\; \mathrm{J\, K^{-1} mol^{-1}} \times 298 \, \text{K} \times \ln K \nonumber \]
\[ \dfrac{-541\; \mathrm{J \, mol^{-1}}}{-8.314\; \mathrm{J\, K^{-1}\, mol^{-1}} \times 298 \, \text{K}} = \ln K \nonumber \]
\[K = 1.25 \nonumber \]
b. The \( \Delta G\) of formation for the compounds are
FeCl3(s) = -334.0 J mol-1, FeCl2(s) = -302.3 J mol-1, Cl(g)=105.3 J mol-1
The calculations are
\[ \Delta G_{\text{rxn}} = (-302.3\; \mathrm{J\, mol^{-1}} + 105.3\; \mathrm{J\, mol^{-1}}) + 334.0\; \mathrm{J\, mol^{-1}} =137\; \mathrm{J\, mol^{-1}} \nonumber \]
\[ 137\; \mathrm{J \, mol^{-1}} = -8.314\; \mathrm{J \, K^{-1} \, mol^{-1}} \times 298 \, \mathrm{K} \times \ln K \nonumber \]
\[ \dfrac{137\; \mathrm{J \, mol^{-1}}}{-8.314\; \mathrm{J \, K^{-1} \, mol^{-1}} \times 298 \, \mathrm{K}} = \ln K \nonumber \]
\[ K = 0.945 \nonumber \]
c. The \( \Delta G\) of formation for the compounds are
CaSO4(s)= -1322.0 J/mol, Ca2+(aq) = -553.58 J/mol, SO42-(aq) = -744.53 J/mol
The calculations are
\[\Delta G_{\text{rxn}} = (-553.58\; \mathrm{J \, mol^{-1}} - 744.53\; \mathrm{J\, mol^{-1}}) + 1322.0\; \mathrm{J\, mol^{-1}} = 23.89\; \mathrm{J\, mol^{-1}} \nonumber \]
\[ 23.89\; \mathrm{J\, mol^{-1}} = -8.314\; \mathrm{J\, K^{-1}\, mol^{-1}} \times 298 \, \text{K} \times \ln K \nonumber \]
\[ \dfrac{23.89\; \mathrm{J\, mol^{-1}}}{-8.314\; \mathrm{J\, K^{-1}\, mol^{-1}} \times 298 \, \text{K}} = \ln K \nonumber \]
\[ K = 0.99 \nonumber \]
Q17
To ignite this house on fire, you dowsed the house in some ethanol and used a combustion reaction:
\[ \ce{C2H5OH(l) + O2(g) <=> H2O(l) + CO2 (g)}\nonumber \]
This reaction has an equilibrium constant of K1. If you multiply this equation by 5, will the equilibrium constant change? If so, write this new equilibrium constant, K2, in terms of K1.
- Solution
-
Because:
\(K = \ce{\dfrac{[A]^{a}[B]^{b}}{[C]^{c}[D]^{d}}}\)
If we multiply a chemical equation by a constant, the exponents of K will be multiplied by that multiple as well.
For this question, first balance this chemical equation, \[ \ce{C2H5OH(l) + 3 O2(g) <=> 3 H2O(l) + 2 CO2 (g)}\nonumber \] the corresponding equilibrium constant is \[ K_1 = \ce{\frac{[CO2]^2}{[O2]^3}} \nonumber\] since liquid is ignored.
When we multiply this equation by 5, the chemical equation becomes, \[ \ce{5 C2H5OH(l) + 15 O2(g) <=> 15 H2O(l) + 10 CO2 (g)}\nonumber\] the corresponding equilibrium constant is \[ K_2 = \ce{\frac{[CO2]^10}{[O2]^15}} = \left(\ce{\frac{[CO2]^2}{[O2]^3}}\right)^5 \nonumber\]
Therefore, for this reaction, the equilibrium constant changes and \(K_2 = K_1^5\).
Q21
An unknown gas B5D10 reacts at room temperature and becomes B10D20, the reaction is illustrated with the equation
\[\ce{2 B5D10(g) <=> B10D20(g)} \nonumber \]
At room temperature the equilibrium partial pressure of B5D10 is \(1.23 \times 10^{-4} \, \text{atm}\) and that of B10D20 is \(3.14 \times 10^{-16} \, \text{atm}\). Given these constants, what is \(K_p\) of this reaction at room temperature.
- Solution
-
Given that we already know the partial pressures and this reaction is at equilibrium, we simply substitute the values into the equilibrium equation and solve for Kp.
\[ K_p=\dfrac{[\text{products}]}{[\text{reactants}]}\nonumber \]
\[ K_p=\dfrac{[3.14 \times 10^{-16}]}{[1.23 \times 10^{-4}]^2}=2.08 \times 10^{-8}\nonumber \]
\[ K_p=2.08 \times 10^{-8}\nonumber \]
Q23A
Suppose there exists a compound that can be found in two forms, red and blue, such that
\[\ce{X_{red} <=> X_{blue}}\nonumber \]
During equilibrium at 25.0°C, 17% of the substance is determined to be in blue form. What is the equilibrium constant for this reaction?
- Solution
-
The equilibrium constant, \(\ce{K_{eq}}\), for the chemical equation
\[\ce{X_{red} <=> X_{blue}}\nonumber \]
can be calculated by constructing the following equation:
\[ \ce{K_{eq}} = \frac{ \left[ \ce{X_{blue}} \right] }{ \left[ \ce{X_{red}} \right] } \nonumber \]
Given that 17% of the concentration is \(\ce{X_{blue}}\), that means the remaining 83% is \(\ce{X_{red}}\), which can be plugged into the equation to yield
\[ \ce{K_{eq}} = \frac{ \left[ 0.17 \right] }{ \left[0.83 \right] } = 0.205 \nonumber \]
which can be further reinforced by viewing it as the fact that since \( \ce{K_{eq}} \lt 1\), the concentration of products present is expected to be smaller than the concentration of reactants.
Q23B
1,2-dimethylcyclohexane can exist in both boat and chair conformation. There is equilibrium between the two forms. What is the equilibrium constant for the reaction of boat conformation to chair conformation if the molecules in the boat form are 68.7%?
- Solution
-
\[ \ce{[Boat] -> [Chair]} \nonumber\]
Let B stand for Boat and C stand for Chair, then the equilibrium constant for this reaction is
\[K=\ce{\frac{[C]}{[B]}} \nonumber\]
For [C] and [B] here, we can use the molar concentration \(c = n / V\), then \[\ce{[C]} = n(\ce{C}) / V \nonumber\] \[\ce{[B]} = n(\ce{B}) / V \nonumber\] So \[K = \frac{n(\ce{C}) / V}{n(\ce{B}) / V} = \frac{n(\ce{C})}{n(\ce{B})} = \frac{n(\ce{C}) / n_{\text{tot}}}{n(\ce{B}) / n_{\text{tot}}} \nonumber\]
From the question, it consists only with boat and chair conformation, so \(n(\ce{C}) / n_{\text{tot}} = 0.687\), and the remaining is for boat, so \(n(\ce{B}) / n_{\text{tot}} = 1 - 0.687 = 0.313\).
Therefore, the equilibrium constant is \[K = \frac{n(\ce{C}) / n_{\text{tot}}}{n(\ce{B}) / n_{\text{tot}}} = \frac{0.687}{0.313} = 2.19 \nonumber\]
Q28
The \(K_p\) for the following reaction is 3.0 at 1000 K.
\[\ce{CO2(g) + C(s) <=> 2 CO(g)} \nonumber \]
- If the pressure in the container where the reaction occurs was initially 0.48 bar, calculate the partial pressures of \(\ce{CO2}\) and \(\ce{CO}\) at equilibrium.
- Calculate the percentage of \(\ce{CO2}\) that has been dissociated.
- Solution
-
a)
\[ \ce{CO2 (g) + C(s) <=> 2CO (g)} \nonumber\]
\(\ce{CO2 (g)}\) \(\ce{CO (g)}\) Initial 0.48 0 Change \(-x\) \(+2x\) Equilibrium \(0.48 - x\) \(2x\) \[K_p = \frac{p(\ce{CO})^2}{p(\ce{CO2})} \nonumber\]
⇒ \[ 3 = \frac{(2x)^2}{(0.48-x)} \nonumber \]
⇒ \[4x^2 = 3(0.48-x) \nonumber\]
⇒ \[4x^2 = 1.44 - 3x \nonumber\]
⇒ \[4x^2 + 3x - 1.44 = 0 \nonumber\]
By solving the quadratic equation, the positive value we get is
\[x = 0.33 \nonumber\]
Hence at equilibrium,
\[p(\ce{CO}) = 2x = 0.66 \nonumber\]
\[p(\ce{CO2}) = 0.48 - x = 0.48 - 0.33 = 0.15 \, \text{bar}\nonumber\]
b) For fraction that has not reacted,
\[\frac{p(\ce{CO2(final)})}{p(\ce{CO2(initial)})} \times 100 \% \nonumber\]
The unreacted percentage is
\[= \frac{0.15}{0.48} \times 100 \% = 31.25 \% \nonumber \]
Hence, 68.75% of the CO2 has reacted.
Q29
A 100.0 mL glass bulb was filled which a weighed sample of solid \(\ce{XO3}\), where \(\ce{X}\) is an unknown element. The bulb was then attached to a pressure gauge and heated to 325 K, at which, the pressure was read to be 0.891 atm. Given that all of the \(\ce{XO3}\) in the bulb at 325 K was in the gas phase, and it also partially dissociated into \(\ce{O2 (g)}\) and \(\ce{XO (g)}\):
\[\ce{XO3 (g) <=> O2 (g) + XO (g)} \nonumber \]
At 325 K, Kp = 3.14 for this reaction. Calculate the partial pressures of all three species in the bulb at equilibrium.
- Solution
-
\[\ce{XO3 (g) <=> O2 (g) + XO (g)} \nonumber\]
Let Y be the initial partial pressure of X2O5, and x is the change in partial pressure of O2:
ICE \(\ce{XO3}\) \(\ce{O2}\) \(\ce{XO}\) Initial \(y\) 0 0 Change \(-x\) \(+x\) \(+x\) Equilibrium \(y-x\) \(x\) \(x\) The total pressure is 0.891 atm, therefore:
\[ (y - x) + x + x = 0.891 \, \text{atm} \nonumber \]
\[ y + x = 0.891 \, \text{atm} \nonumber \]
\[ y = 0.891 - x \nonumber \]
So the ICE table now would be:
ICE \(\ce{XO3}\) \(\ce{O2}\) \(\ce{XO}\) Initial \(0.891 - x\) 0 0 Change \(- x\) \(+ x\) \(+ x\) Equilibrium \(0.891 - 2x\) \(x\) \(x\) \[ K_{p} = 3.14 = \dfrac{P_{\ce{XO}} \cdot P_{\ce{O2}}}{P_{\ce{XO3}}} = \dfrac{x^2}{0.891 - 2x} \nonumber\]
\[ x^2 + 6.28x - 2.80 = 0 \nonumber\]
\[ x = 0.418 \nonumber\]
\[ P_{\ce{O2}} = P_{\ce{XO}} = 0.418 \, \text{atm} \nonumber\]
\[ P_{\ce{XO3}} = 0.891 - 2(0.418) = 0.055 \, \text{atm} \nonumber\]
Q31
The equilibrium constant \(K_c\) for the reaction
\[\ce{F2(g) + H2(g) <=> 2 HF(g)}\nonumber \]
at 298 K is \(5.07 \times 10^4\). Hydrogen with a partial pressure of 0.03500 atm is mixed with fluorine with a partial pressure of 0.06800 atm, and allowed to reach the equilibrium. What is the partial pressure of each of the gasses at the equilibrium?
- Solution
-
We are looking for partial pressures of the reactants and we have starting partial pressures and a \(K_c\) value. First we need to convert \(K_c\) to \(K_p\)
\[K_p = K_c (RT)^{\Delta{n_{\text{gas}}}}\nonumber \]
\[ K_p = (5.07 \times 10^4) \times (0.0821 \times 298 \, \text{K})^{0} = 5.07 \times 10^4 \nonumber \]
The equilibrium constant can be constructed from the equation given
\[K_p = \ce{\dfrac{[HF]^2}{[H2][F2]}} \nonumber \]
Use an ICE table to find the equilibrium partial pressures of the equilibrium
Reaction \(\ce{H2 (g)}\) \(\ce{F2 (g)}\) \(\ce{2HF (g)}\) I \(0.035\) \(0.068\) \(0\) C \(-x\) \(-x\) \(+2x\) E \(0.035-x\) \(0.068-x\) \(2x\) \[5.07 \times 10^4 = \dfrac{[2x]^2}{[0.035 - x]^2[0.068 - x]^2} \nonumber\]
Simplify the equation and solve as you wish. You can't use the quadratic formula because you end up with a degree three equation but you can put the equation into a graphing calculator and solve for \(x\) using the zero function.
\[x = 0.0286 \, \text{atm} \nonumber\]
\[ \ce{[HF]} = 2 x = 0.0571 \, \mathrm{atm} \nonumber \]
\[ \ce{[H2]} = 0.035 - x = 0.00643 \, \mathrm{atm} \nonumber \]
\[ \ce{[F2]} = 0.068 - x = 0.0394 \, \mathrm{atm} \nonumber \]
Q33
At 25 °C, the equilibrium constant for the reaction below has the value of \(1.7 \times 10^{-13}\):
\[\ce{ N2O(g) + 1/2 O2(g) <=> 2 NO(g)} \nonumber \]
In a container where \(\ce{N2O}\) has an initial partial pressure of 0.62 atm, \(\ce{O2}\) has a pressure of 0.24 atm, and \(\ce{NO}\) has an initial pressure of 0.08 atm, what will the partial pressure of the three gases be after reaching equilibrium at the same temperature?
Q35
The reaction:
\[\ce{2HI(g) <=> H2(g) + I2(g)} \nonumber \]
has an equilibrium constant \(K_c = 1.82 \times 10^{-2}\) at 698 K. If the reaction took place in a tank at 698 K and started off with HI having a partial pressure of 1 atm, what would the partial pressures of all the gases be at equilibrium?
- Solution
-
First, we need to convert \(K_c\) into \(K_p\) with the equation
\[K_p = K_c (RT)^{\Delta n} \nonumber\]
\[K_p = 1.82 \times 10^{-2} (0.0821 \, \text{L atm / K mol} \times 698 \, \text{K})^{2-2} \nonumber\]
\[K_p = 1.82 \times 10^{-2} \nonumber\]
An ICE table can also be constructed for the reaction:
\[\ce{2HI (g) <=> H2 (g) + I2 (g)} \nonumber \]
ICE Table \(\ce{2HI (g)} \) \(\ce{H2(g)}\) \(\ce{I2(g)}\) Initial 1
0
0
Change \(-2x\)
\(+x\)
\(+x\)
Equilibrium \(1-2x\)
\(x\)
\(x\)
\[0.82 \times 10^{-2} = \dfrac{x^2}{1-2x} \nonumber\]
\[x^2 = 1.82 \times 10^{-2} - 0.0368 x \nonumber\]
\[x = 0.118488 \nonumber\]
\[\text{partial pressure of } \ce{HI} = 0.763 \, \text{atm} \nonumber\]
\[\text{partial pressure of } \ce{H2} = \text{partial pressure of } \ce{I2} = 0.1189 \, \text{atm} \nonumber\]
Q37
What is the concentration of a \(\ce{XY}\) that will be found in equilibrium at room temperature, given that \(\ce{X2}\) has a concentration of \(3.14 \times 10^{-15} \, \text{M}\), \(\ce{Y2}\) has a concentration of \(1.23 \times 10^{-4}\, \text{M}\), and the \(K_c\) of the reaction is \(2.22 \times 10^{-7} \, \text{M}\).
- Solution
-
First we must state what the formulas for both the reaction and Kc and then we can substitute the known values and solve for the concentration of XY as an unknown variable.
\[\ce{2XY(g) <=> X2 (g) + Y2(g)} \nonumber \]
\[ K_c = \mathrm{\dfrac{[Products]}{[Reactants]}} \nonumber \]
\[ K_{c}= \ce{\dfrac{[X2] [Y2]}{[XY]^2}} = \dfrac{[3.14\times10^{-15}][1.23\times10^{-4}]}{\ce{[XY]}^{2}}=2.22\times10^{-7} \nonumber \]
\[ K_{c}=\dfrac{[3.86\times10^{-19}]}{\ce{[XY]}^{2}}=2.22\times10^{-7} \nonumber \]
\[ K_{c}=3.86\times10^{-19}=2.22\times10^{-7}\ce{[XY]}^{2} \nonumber \]
\[ \ce{[XY]}=1.32 \times 10^{-6} \nonumber \]
So the concentration of \(\ce{XY}\) is \(1.32 \times 10^{-6} \, \text{M}\) in equilibrium at 25ºC.
Q41
Hydrogen and oxygen gas react with each other to form gaseous water with an equilibrium constant for the reaction is \(K_c = 1.33 \times 10^{20}\) at 1000 K.
- Consider a system at 1000.0 K in which 4.00 atm of oxygen is mixed with 0.500 atm of hydrogen and no water is initially present. What is the concentration of hydrogen gas after equilibration.
- Consider a system, also at 1000.0 K, where 0.250 atm of oxygen is mixed with 0.500 atm of hydrogen and 2.000 atm of water. What is the concentration of hydrogen and oxygen gas after equilibration.
- Solution
-
a)\[\ce{2 H2 (g) + O2 (g) <=> 2 H2O(l)} \nonumber\]
\[K=3.4 = \frac{1}{P_{\ce{H2}}^2 P_{\ce{O2}}} \nonumber\]
\[P_{\ce{H2}}=1.2\, \text{atm} \nonumber\]
\[3.4 = \frac{1}{(1.2)^2 P_{\ce{O2}}} \nonumber\]
\[P_{\ce{O2}}=\frac{1}{(1.2)^2 (3.4)}= 0.204\, \text{atm} \nonumber\]
b) Excess \(\ce{H2O(l)}\) is added drive the reaction to the left towards the reactant to reach the equilibrium; therefore, pressure of H2 and O2 increased.
\(\ce{2H2(g)}\) \(\ce{O2(g)}\) \(\ce{2H2O(l)}\) Initial 0 0.3 N/A Change \(+2x\) \(+x\) N/A Equilibrium \(2x\) \(0.3+x\) N/A \[K=\frac{1}{(2x)^{2}(0.3+x)}=3.4 \nonumber\]
\[3.4(0.3+x)(2x)^{2}=1 \nonumber\]
\[x=0.339\, \text{atm} \nonumber\]
\[P_{\ce{O2}}=0.3+0.339=0.639\, \text{atm} \nonumber\]
\[P_{\ce{H2}}=2(0.339)=0.678\, \text{atm} \nonumber\]
Q43
If you decompose ammonium nitrate into water and nitrous oxide, which further decomposes into oxygen and nitrogen gas, making the final reaction:
\[\ce{ 2 NH4NO3(s) <=> 2 N2(g) + O2(g) + 4 H2O(g)} \nonumber \]
This reaction takes place only in the molten salt, above its melting point of 169.6°C (for the anhydrous product). So, you get your 170°C blow torch and begin decomposing the ammonium nitrate under a sealed hood. Upon decomposition, all of the ammonium nitrate is gone, i.e. the reaction goes to completion.
- What can be said of the equilibrium constant of this reaction at 170°C?
- Now, in another universe, the partial pressure of N2(g) is 0.3 atm initially. Will the reaction still go to, essentially, completion?
- Solution
-
(a) If there is no ammonium nitrate left, then the reaction was heavily products favoring, meaning K is extremely high at 170°C.
Note: It's more accurate to say that Q is a big number when there is no reactants left after reaction occurred. Reviewer's comment: Q stands for the current state. K is the equilibrium constant. When there is no reactant left after reaction occurred, the reaction is at the equilibrium state, so Q = K. Since Q is a big number, then K is also a big number.
(b) There would have to be an enormous amount of Nitrogen to force the reaction backwards. Because 0.3 atm is likely not enough to push back an essentially irreversible reaction, it has no noticeable affect on the amount of end product. (Note: If the reactants and products are essentially gas, we calculate the equilibrium constant not by its concentration, but by its pressure.)
Q45
Al2Cl6 at a partial pressure of 0.600 atm is placed in a closed container at 454 K. Al3Cl9 (partial pressure \(1.98 \times 10^{-3} \, \text{atm}\)) is also placed in it as well. Argon is added to raise the total pressure up to 1.00 atm.
Find whether if there is going to be net production or consumption of Al3Cl9 given \(K_p = 1.04 \times 10^{-4}\). Then find the final pressure of Al3Cl9.
- Solution
-
The reaction is \[\ce{ 3 Al2Cl6 (g) <=> 2 Al3Cl9 (g)} \nonumber\] Because argon does not react, it can be ignored.
\[Q=\frac{(\ce{[Al3Cl9]})^{2}}{(\ce{[Al2Cl6]})^{3}}= \frac{(1.98 \cdot 10^{-3})^{2}}{(0.600)^{3}}=1.82 \cdot 10^{-5} < K_p = 1.04 \cdot 10^{-4} \nonumber\]
There will be production of Al3Cl9.
ICE Table Al2Cl6 Al3Cl9 Initial 0.600 \(1.98 \times 10^{-3}\) Change \(-3y\) \(+2y\) Equilibrium \(0.6 - 3y\) \(1.98 \times 10^{-3} + 2y\) \[K= 1.04 \cdot 10^{-4} \frac{(\ce{[Al3Cl9]})^{2}}{(\ce{[Al2Cl6]})^{3}}= \frac{(1.98 \times 10^{-3} + 2y)^{2}}{(1 - (1.98 \times 10^{-3} + 2y))^{3}} \nonumber\] Solving out \[y = 0.0041 \, \mathrm{atm} \nonumber\]
Al3Cl9 final pressure = 0.0102 atm.
Q46
The thermal decomposition of NH4Cl solid proceeds as follows:
\[\ce{NH4Cl(s) <=> NH3(g) + HCl(g)} \nonumber\]
the equilibrium constant at 275°C is \(1.04 \times 10^{-2}\). If the partial pressures of \(\ce{NH3(g)}\) and \(\ce{HCl(g)}\) are equal, and the total partial pressure of the system is 0.200 atm, in what direction does the reaction proceed? What will be formed?
- Solution
-
First, we make two equations to solve out the partial pressures. To get the first equation, we sum over the partial pressures to the total pressure. \(\ce{NH4Cl}\) is a solid, so it doesn't contribute to the partial pressure
\[P_{\ce{NH3}} + P_{\ce{HCl}} = 0.200 \, \mathrm{atm} \nonumber\]
The second equation is from the question that partial pressures of \(\ce{NH3(g)}\) and \(\ce{HCl(g)}\) are equal
\[P_{\ce{NH3}} = P_{\ce{HCl}} \nonumber\]
Hence, \[P_{\ce{NH3}} = P_{\ce{HCl}} = 0.100 \, \mathrm{atm} \nonumber\]
\[Q(\text{reaction quotient}) = P_{\ce{NH3}}P_{\ce{HCl}} = {(0.100)^2}\nonumber\]
\[ 10^{-2} < 1.04 \times 10^{-2}\nonumber\]
\[Q < K\nonumber\]
Hence, the reaction will slightly proceed more in the forward direction.
NH3 and HCl will be formed.
Q47
A tube contains a mixture of NO2 and N2O4 gas is set at 298K, in which the initial partial pressure NO2 is 0.38 atm, and the initial partial pressure of N2O4 is 0.59 atm. NO2 is a brownish gas, while N2O4 is a colorless gas.
\[ \ce{2NO2(g) \rightleftharpoons N2O4(g)} \nonumber \]
- What is the reaction quotient at the start of this reaction?
- As the reaction shown above reaches equilibrium, the mixture becomes more brown. With this in mind, is the equilibrium constant, Kp, greater than or less than the Q calculated in part a?
- Solution
-
a) \[\ce{2 NO2 (g) \rightleftharpoons N2O4(g)} \nonumber\]
\[P_{\ce{N2O4}} = 0.59 \; \text{atm} \quad P_{\ce{NO2}} = 0.38 \; \text{atm} \nonumber \]
\[ Q_{p} = \frac{P_{\ce{N2O4}}}{(P_{\ce{NO2}})^{2}} \nonumber\]
\[ Q_{p} = \frac{0.59}{0.38^{2}} = 4.1 \nonumber\]
b) Since the mixture becomes more brown as the reaction reaches equilibrium, more NO gas is being produced, therefore the reverse reaction is favored, so Qp > kp, in conclusion, Kp < 4.1.
Q49
At 500 K the equilibrium constant for the reaction:
\[\ce{ PCl3 (g) + Cl2 (g) <=> PCl5 (g)} \nonumber\]
is \(K_{eq}=2.1\). Suppose the equilibrium is disturbed and shifts, while temperature remains constant. Calculate the reaction quotient for each one of the possible changes in equilibrium concentration given below and evaluate in what direction the reaction will shift to reestablish equilibrium.
- [PCl3]= 0.0563, [Cl2]= 0.0784, [PCl5]= 0.8934.
- [PCl3]=0.4390 , [Cl2]= 0.3547, [PCl5]= 0.1048.
- [PCl3]= 0.4018, [Cl2]= 0.8690, [PCl5]= 0.7205.
Q48
NO2 has a brownish color. At elevated temperatures, NO2 reacts with CO
\[\ce{NO2 (g) + CO (g) <=> NO(g) + CO2 (g)}\nonumber \]
The other gases in this equation are colorless. When a gas mixture is prepared at 600K, in which 9.6 atm is the initial partial pressure of both NO2 and CO, and 5.4 atm is the partial pressure of both NO and CO2, the brown color of the mixture observed begins to get stronger as the reaction progresses toward equilibrium. Give a condition that must be satisfied by the equilibrium constant K.
Q51
The equilibrium constant (\(K_p\)) for the reaction
\[ \ce{As4(g) <=> 2 As2(g)} \nonumber \]
is \(5.5837 \times 10^{-4}\) at 1090 K.
- The initial molarity of \(\ce{[As4]}\) is 2.3 M and the initial molarity of \(\ce{[As2]}\) is 0.001 M. Calculate the reaction quotient \(Q\) and determine which way the reaction proceeds.
- Calculate the molarity of each compound at the equilibrium.
- Which direction will the reaction proceed if the pressure on the reaction decreases? Explain your answer.
- Solution
-
(a) First, because you are given the initial molarities of your products and reactants and a Kp instead of a Kc value, you have to convert Kp to Kc using the formula:
\[K_p = K_c(RT)^{\Delta{n_{\text{gas}}}}\nonumber \]
Plug in your given values
\[5.5837 \times 10^{-4} = K_c (0.0821 \times 1090)^{2-1} = 89.489 K_c \nonumber\]
\[K_c = 6.24 \times 10^{-6} \nonumber\]
Set up a reaction quotient for the equation given
\[Q = \ce{\frac{ [As2]^2}{[As4]}} = \frac{[0.001]^2}{[2.3]} = 4.35 \times 10^{-7} \nonumber\]
Reaction will progress towards the right to reach equilibrium
(b) Set up an ice chart to find the equilibrium molarities
Reaction P4 2 P2 I 2.3 0.001 C \(-x\) \(+2x\) E \(2.3-x\) \(0.001+2x\) \[6.24 \times 10^{-6} = \frac{[0.001+2x]^2}{[2.3-x]} \nonumber\]
\[4x^2 + 0.00400624 x - 1.3352 \times 10^{-5} = 0 \nonumber\]
Use the quadratic equation to find \(x\)
\[x= -0.0024, 0.00139 \nonumber\]
-0.0024 is negative, which can't happen in real life so we know \(x) actually equals 0.00139.
[P4]= 2.29861 M
[P2]= 0.00378 M
(c) The reaction will progress towards the right because as pressure decreases, the reaction moves towards the side with the most moles of gas, which is the products.
Q55
Consider a reaction involving only gaseous compounds. The product yield at equilibrium decreases when the temperature and volume increase.
- Is this reaction endothermic or exothermic?
- Does the number of gas molecules in this reaction increase or decrease?
- Solution
-
a. Exothermic. In exothermic reactions, product yield is indirectly related to temperature. In endothermic reactions, product yield is directly related to temperature. These properties can be further explained when heat is thought of as a reactant or a product. In exothermic reactions, heat is a product, and in endothermic reactions, heat is a reactant. When heat is added to a reaction, the equilibrium shifts to the opposite side to relieve stress on the system.
b. Decreases. The number of gas molecules is directly related to the volume of the container in which the reaction is happening. For example, if the volume of the container is decreased, the reaction will shift to whichever side has fewer moles of gas.
Q57
the Haber process, also called the Haber–Bosch process, is an artificial nitrogen fixation process and is the main industrial procedure for the production of ammonia today.
\[ \ce{N3 + 3H2 <=> 2NH3} \quad (\Delta H = -92.4\, \mathrm{kJ/mol}) \nonumber\]
Determine the best condition of temperature and pressure to yield the most ammonia.
- Solution
-
Because Haber process is an exothermic reaction, a lower temperature will maximize the yield of product. Also, according to the ideal gas law, because the moles of gas are proportional to the volume, and the volume is inverse proportional to the pressure; a higher pressure is required to maximize the yield of product.
Q59
At room temperature, a vessel is filled with gaseous carbon dioxide. Some water is added at 2.00 atm. It is well-shaken, integrating carbon dioxide gas into the water. 0.5 kg of the solution is taken out and boiled to extract 2.50 L of carbon dioxide. The system is at 10 degree Celsius and 1.00 atm. What is the Henry’s Law constant for carbon dioxide in water?
- Solution
-
given that the extracted solution:
\[PV=nRT\]
\[n = \frac{PV}{RT}=\frac{1 \, \text{atm} \times 2.5 \, \text{L}}{0.082 \mathrm{\frac{L\, atm}{mol\, K}} \times 283.15 \, \mathrm{L}}=0.1077 \, \mathrm{mol}\]
\[m_{\ce{CO2}}=n_{\ce{CO2}} \times \text{molar mass} = 0.1077\, \mathrm{mol} \times 44\, \mathrm{g/mol} = 4.7388\, \mathrm{g}\]
\[m_{\ce{H2O}}=500\, \text{g} - 4.7388\, \text{g} = 495.29\, \text{g}\]
\[n_{\ce{H2O}} = \frac{495.29\, \mathrm{g}}{18\, \mathrm{g/mol}} = 27.5 \, \text{mol}\]
\[\text{Solubility of \ce{CO2} in water} = \frac{0.1077\, \text{mol}}{0.5\, \text{kg}}=0.2154 \, \mathrm{mol/kg}\]
Due to the Ideal gas law, the ratio of moles equals to the ratio of pressure
pressure: pressure = mol:mol = 0.1077: 27.51
because the total pressure is 2 atm, partial pressure of CO2 = 0.0724 atm
Due to Henry's law:
\[k=\frac{c}{P}=\frac{0.2154mol/kg}{0.0724\ atm}=2.9751\frac{mol}{kg\ atm}\]
Q61
The equilibrium constant for a reaction increases from \(\ce{K= 4.5 \times 10^{-2}}\) to \(\ce{K= 4.5}\) as the temperature increases from \(0.00\text{°C}\) to \(300.0\text{°C}\). Assuming the change in enthalpy (\(\ce{\Delta}\text{H}\)) and change in entropy (\(\ce{\Delta}\text{S}\)) are constant over this range of temperatures, what is \(\ce{\Delta}\text{S}\) for this reaction? Is this reaction endothermic or exothermic?
- Solution
-
Assuming \(\ce{\Delta}\text{H}\) and \(\ce{\Delta}\text{S}\) are constant, we can set up a system of equations as follows:
\( \{\begin{array}{ll} \ce{\Delta}{G_{0.00\text{°C}}} = {\Delta}\text{H} - \text{T}{\Delta}\text{S} \\ {\Delta}{G_{300.0\text{°C}}} = {\Delta}\text{H} - \text{T}{\Delta}\text{S} \\ \end{array} \)
We can determine \(\ce{\Delta}{G_{0.00\text{°C}}}\) and \(\ce{\Delta}{G_{300.0\text{°C}}}\) by utilizing the equation below that relates \(\ce{\Delta}{G}\) to \(\ce{K_{eq}}\):
\(\ce{\Delta}{G} \ = \ -\text{RT ln(K)}\) Easily remembered using the mnemonic: "\({\Delta}\text{G}\)et in the \(-\text{R}\)igh\(\text{T}\) \(\text{l}\)a\(\text{n}\)e, \(\text{K}\)?"
\( \ce{\Delta}{G_{0.00\text{°C}}} \ = \ - \left(8.314 \frac{\text{J}}{\text{K} \times \text{mol}} \right) \left( 273.15 \text{K} \right) \left( \text{ln}( 4.5 \times 10^{-2}) \right)\ = \ 7042.5 \frac{\text{J}}{ \text{mol}} \)
\( \ce{\Delta}{G_{300.0\text{°C}}} \ = \ - \left(8.314 \frac{\text{J}}{\text{K} \times \text{mol}} \right) \left( 573.15 \text{K} \right) \left( \text{ln}( 4.5) \right)\ = \ -7167.2 \frac{\text{J}}{ \text{mol}} \)
These values can then be plugged back into the original system of equations to obtain
\( \{\begin{array}{ll} \ce{\Delta}{G_{0.00\text{°C}}} = 7042.5 \frac{\text{J}}{\text{mol}} = {\Delta}\text{H} - \left( 273.15 \text{K} \right) {\Delta}\text{S} \\ {\Delta}{G_{300.0\text{°C}}} = -7167.2 \frac{\text{J}}{ \text{mol}} = {\Delta}\text{H} - \left( 573.15 \text{K} \right) {\Delta}\text{S} \\ \end{array} \)
To calculate the values of the remaining two unknown variables, a substitution can be made that expresses \(\ce{\Delta}\text{H}\) in terms of \(\ce{\Delta}\text{S}\).
\(-7167.2 \frac{\text{J}}{\text{mol}} + \left( 573.15 \text{K} \right) {\Delta}\text{S} = {\Delta}\text{H} \)
This substitution can be plugged into the first equation to calculate the value for \(\ce{\Delta}\text{S}\).
\( 7042.5 \frac{\text{J}}{\text{mol}} = -7167.2 \frac{\text{J}}{\text{mol}} + \left( 573.15 \text{K} \right) {\Delta}\text{S} - \left( 273.15 \text{K} \right) {\Delta}\text{S} \)
\( {\Delta} \text{S} = 47.37 \frac{\text{J}}{\text{K} \times \text{mol}} \)
\(\ce{\Delta}\text{H}\) can be calculated now by plugging in the value for \( {\Delta} \text{S} \) into either one of the equations in the original set.
\( 7042.5 \frac{\text{J}}{\text{mol}} = {\Delta}\text{H} - \left( 273.15 \text{K} \right) \left( 47.37 \frac{\text{J}}{\text{K} \times \text{mol}} \right) \)
\( \ce{\Delta}\text{H} = 19980 \frac{\text{J}}{\text{mol}} = 19.98 \frac{\text{kJ}}{\text{mol}} \)
Because \(\ce{\Delta}\text{H}\) is positive, we know the reaction is endothermic.
Q63A
The equilibrium constant for the reaction \(\ce{N2O4(g) <=> 2 NO2(g)}\) is measured to be \(5.9\times10^{-3}\) at 298\;K and \(1.3\times10^{-6}\) at \(398\;K\)
- Calculate \(\Delta G^{\circ}\) at 298 K for the reaction.
- Calculate \(\Delta H\) and \(\Delta S^{\circ}\), assuming the enthalpy and entropy changes are independent of temperature between 298 K and 398 K.
- Solution
-
a.Use the equation \(\Delta G^{\circ}=-RT\ln K\)
\(\Delta G^{\circ}=-RT \ln K=(-8.3145\; \mathrm{J \, K \, mol^{-1}}) \times (298\; \mathrm{K})(\ln 5.9 \times 10^{-3})=-1.29\times10^{4}\; \mathrm{J\, mol^{-1}}\)
For one mole of the reaction as written, \(\Delta G^{\circ}\) is -1290 kJ.
b. Use van't Hoff equation and the values of K at 298 K and at 398 K to obtain \(\Delta H^{\circ}\). Then get \(\Delta S^{\circ}\) from \(\Delta G^{\circ}\) and the equation \(\Delta G^{\circ}=-RT \ln K\)
\(\ln(\frac{1.3 \times 10^{-6}}{5.9 \times 10^{-3}})=\frac{\Delta H^{\circ}}{8.3145\; \mathrm{J\,K^{-1} \, mol^{-1}}}(\frac{1}{398\;K}-\frac{1}{298\;K})\)
\(\Delta\;H^{\circ}=83.0\;kJ\)
The answer equals both \(\Delta\;H^{\circ}\) at 298 K and 398 K because it is assumed in the derivation of the van't Hoff equation that \(\Delta\;H^{\circ}\) is independent of temperature. Next,
\(\Delta\;S^{\circ}=\frac{\Delta\;H^{\circ}-\Delta\;G^{\circ}}{T}=\frac{83.0\times10^{3}\;J-(-1.29\times10^{4}\;J)}{298\;K}=323\;J\;K^{-1}\)
Q63B
For the reaction: \(\ce{ Br2(g) <=> 2Br(g)}\), the equilibrium constant is \(4.64 \times 10^{-29}\) at 25oC and \(1.1 \times 10^{-3} \) at 1280 K.
- What is ∆G of the reaction at 298 K?
- Assuming that \(∆H^o\) and \(∆S^o\) are independent of temperature, what are the values of enthalpy and entropy when the temperature changes to 1280 K?
- Solution
-
a. ∆G = RTln(k)
= (8.3145JK-1mol-1)(298K)ln(4.64x10-29)
= -161.65kJ
a) \[ ln \left(\dfrac{1.1x10^{-3}}{4.64x10^{-29}}\right) = \dfrac{-∆ H}{R} \left( \dfrac{1}{1280K} - \dfrac{1}{298K} \right) \nonumber \]
Solve for ∆ H.
∆ H = 188.70 KJ
\[ln \left({k}\right) = \dfrac{-∆ H}{RT} + \dfrac{ ∆S}{R} \nonumber \]
\[ln \left({1.1x10^{-3}}\right) = \dfrac{-188699.30}{(8.3245;\ {JK^{-1}mol^{-1})(1280:\K} + \dfrac{ ∆S}{R} \nonumber \]
∆S =90.78 JK-1mol-1
Q65
Calculate the equilibrium constant for the reaction,
2 NO2 (g) \( \rightleftharpoons \) N2O4 (g) at 500 K,
given the equilibrium constant K = 4.65 x 10-3 at 298 K, and ΔH° = -57.2 kJ mol-1. Assume that ΔH° does not change between 298 K and 500 K
- Solution
-
Use the van 't Hoff equation to calculate K500 from K298 and the standard enthalpy of the reaction ΔH°:
\[ln \frac{K_{500}}{K_{298}} = - \dfrac{\Delta H°}{R} (\frac{1}{T_{1}} - \frac{1}{T_{2}} ) \nonumber \]
=> K500 = 3.366 x 10-7
Solve for the unknown variable, in this case it is K500. T1 is equal to 298K while T2 is equal to 500K.
Q69
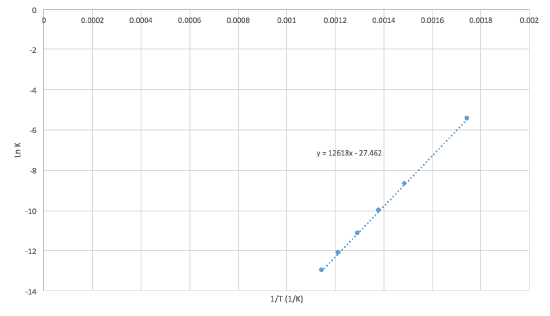
The equilibrium constant for the following reaction was experientially calculated at different temperatures.
\[\ce{N2 (g) + 3H2 (g) \rightleftharpoons 2NH3 (g)} \nonumber \]
| Temperature (°C) | 300 | 400 | 450 | 500 | 550 | 600 |
| Equilibrium Constant (Keq) | 4.34 x 10-3 | 1.64 x 10-4 | 4.51 x 10-5 | 1.45 x 10-5 | 5.38 x 10-6 | 2.25 x 10-6 |
- Plot \(\ln K\) as a function of \(1/T\) (K-1)
- What is \(\Delta Hº\) of the equilibrium reaction with ammonia? HINT: use the slope to find the \(\Delta Hº\)
- Solution
-
The graph bellow shows what the graph should look like:
First we must write the van't Hoff equation:\[\ln K = - \dfrac{\Delta{H^o}}{R} \dfrac{1}{T} + \dfrac{\Delta{S^o}}{R}\label{20}\nonumber \]
Writing the equation like this how it can be compared with y = mx + b. With this information we then know that the slope of the graphe is equal to -\(\Delta{H^o}\)/R. So:
\(\Delta{H^o}\) = -mR were R = 8.3145 J K-1mol-1
\(\Delta{H^o}\) = -104.9 kJ mol-1
Q71
At a certain temperature, \(0.5\ \text{mol}\) \(\ce{I_{2\, (aq)}}\) is dissolved in \(2\ \text{L}\) \(\ce{H_{2}O}\) and shaken vigorously in a container with \(2\ \text{L}\) of \(\ce{CCl_4}\), an immiscible liquid. The container is then left to equilibrate during which time the iodine redistributes itself between the layers of \(\ce{H_{2}O}\) and \(\ce{CCl_4}\) as indicated by the following reaction:
\[\ce{I_{2\, (aq)} \rightleftharpoons I_{2} (CCl_4)}\nonumber \]
The final concentration of \(\ce{I_{2\, (aq)}}\) is determined to be \(0.0710\ \text{M}\). What is the partition coefficient \(\left(\text{K}\right)\) for this process?
- Solution
- The word "equilibrate" is a dead giveaway for "ICE Table" so we can establish the following ICE Table based on the information provided for the reaction provided.
-
\(\ce{I_{2\, (aq)} \rightleftharpoons I_{2} (CCl_4)}\)
ICE Table \(\ce{I_{2\, (aq)}} \) \(\ce{I_{2} (CCl_4)}\) Initial \( 0.250 \text{M} \) \( 0 \text{M} \) Change \( - \text{x} \) \( + \text{x} \) Equilibrium \( 0.0710 \text{M} \) \( + \text{x} \) \( \text{x}\) can be calculated by solving the following equation:
\( 0.250 \text{M} - \text{x} = 0.0710 \text{M} \)
\( \text{x} = 0.179 \text{M}\)
This value can then be plugged into the ICE Table to obtain equilibrium values for \(\ce{I_{2\, (aq)}} \) and \(\ce{I_{2} (CCl_4)}\). (Remember that the two liquids are immiscible so the molarity isn't \( 0.125 \text{M}\) as \(\ce{I_{2} (CCl_4)}\) does not contribute to the initial molarity of the solution.)
ICE Table \(\ce{I_{2\, (aq)}} \) \(\ce{I_{2} (CCl_4)}\) Initial \( 0.250 \text{M} \) \( 0 \text{M} \) Change \( - 0.179 \text{M}\) \( + 0.179 \text{M} \) Equilibrium \( 0.0710 \text{M} \) \( + 0.179 \text{M} \) The equilibrium concentrations of \(\ce{I_{2\, (aq)}} \) and \(\ce{I_{2} (CCl_4)}\) can then be plugged into the equilibrium constant expression and solve for the partition coefficient.
\(\text{K} = \frac{ 0.179 \text{M} }{ 0.0710 \text{M} } \)
\(\text{K} = 2.52 \)
Q73
At 25°C, 0.130 g/L of chloroacetic acid (C2H3ClO2) dissolve in of water, and at the same temperature 0.2834 g/L of chloroacetic acid dissolve in 1-octanol.
a. Calculate the following equilibrium constants
\[\ce{C2H2ClO2H(s)} \rightleftharpoons \ce{C2H2ClO2H}_{(aq)} \nonumber \]
\[\ce{C2H2ClO2H(s)} \rightleftharpoons \ce{C2H2ClO2H}_{(octanol)} \nonumber \]
b. Calculate the participation coefficient, \(K\), of the combined reactions.
\[\ce{C2H2ClO2H(aq)} \rightleftharpoons \ce{C2H2ClO2H}_{(octanol)} \nonumber \]
- Solution
-
First, we will need g/L to M so that we can calculate the equilibrium constant.
\[\left(\dfrac{0.130\; \cancel{g\; C_{2}H_{3}ClO_{2}} }{1\;L}\right) \left(\dfrac{1\: mol}{94.494\: \cancel{ g\; C_{2}H_{3}ClO_{2}}} \right) = 0.0013757\; M\nonumber \]
\[\left(\dfrac{0.2834\; \cancel{g\; C_{2}H_{3}ClO_{2}} }{1\;L}\right) \left(\dfrac{1\: mol}{94.494\: \cancel{ g\; C_{2}H_{3}ClO_{2}}} \right) = 3.00x10^{-3}\; M\nonumber \]
\[K = \dfrac{K_{forminde}}{K_{aq}}=\dfrac{3.00 \times 10^{-3}}{0.001376} =2.18\nonumber \]
\[\log_{10} K_{oct/wat} =0.338\nonumber \]
Q75
At 298 K, the two gases NOBr and Br2 have the number of moles of 1.25 and 8.5 x 10-5 at equilibrium with a sufficient amount of solid NO. Determine the equilibrium constant of the reaction:
\[2NOBr_{(g)} \rightleftharpoons 2NO_{(s)} + Br_{2(g)} \nonumber \]
- Solution
-
Use: Pgas = ngas(RT/V)
K = PBr2 / P2NOBr = nBr2 / n2NOBr = 5.44 x 10-5
The volume is needed to solve this problem. It is necessary to find the value of K regardless of it is Kp or Kc.
Q79
At 300 K and 1 atm, N2O4 is partly dissociated into NO2. The density of the equilibrium mixture was 2.076 g/L. What is the degree of dissociation of N2O4 under these circumstances?
- Solution
-
\[N_2O_4(g) \rightarrow 2NO_2(g) \nonumber \]
moles of N2O4 at equilibrium = 1-x moles of NO2 at equilibrium = 2xTherefore, the degree of dissociation of SO3 is 0.8.
(Multiplying number of moles by molar mass to get the total mass)
92*(1- x) + [46*(2x)/ (1+x) ]= [ 2.076 g/L * 0.08206 (L*atm)/(mol*K) ] / 1 atm
On solving the equation, we get the equation, x= 0.8
Q85
The decompressions of calcium carbonate (\(\ce{CaCO3}\)) occurs according to the following reaction:
\[\ce{ CaCO3 (s) \rightleftharpoons CaO(s) + CO2 (g)}\nonumber \]
100 g of solid calcium carbonate (\(\ce{CaCO3}\)) and 50 g of calcium oxide (\(\ce{CaO}\)) are placed in an evacuated round bottom flask that is heated up to 35°C. At this temperature the pressure in the round bottom flask is found to be 0.5 atm.
- What is the equilibrium constant of the decompressions of calcium carbonate (\(\ce{CaCO3}\)) at 35°C?
- If 100 g of calcium oxide (CaO) at 35°C was added to the flask what would be the new total pressure of the flask and why?
- If the pressure in the round bottom flask would to increase to 1.0 atm, then what would would be the new equilibrium constant?
- Solution
-
- First we need to write the equilibrium expression for the reaction: \[K_{eq} = p\ce{CO2}]\] Now we just need to plug in the pressure of CO2: Keq = [0.5] = 0.5
- The total pressure would still be 0.5 atm because solids have an activity of 1 so they don't effect the equilibrium pressure.
- The new equilibrium constant would be 1.0 atm.
Q87
Let's say you have the reaction: \[A(s) + B(g) \leftrightharpoons C(s) + D(g)\nonumber \]
At 25°C, this reaction has an equilibrium constant of 157.2. Find the partial pressures of \(B(g)\) and \(D(g)\) when the total pressure of the system is equal to 4.3 atm.
- Solution
-
First, the equilibrium expression of this reaction is
\[K_c = \frac {D(g)}{B(g)} = 157.2\nonumber \]
Note, the A(s) and C(s) are not included in this expression because they are solids. Solids have an activity equal to 1 which basically means they do not affect the equilibrium of the reaction.
To calculate the partial pressure of our unknowns, we can use Dalton's Law of partial pressures: \[P_A = X_A P_{Total}\nonumber \]
Since we are looking for the partial pressure of each of our gases, and we already have the total pressure of the system, we need to find the mole fraction of each of our gases. To find it, we can manipulate the above equilibrium expression to get: \[D(g) = 157.2 \; B(g)\nonumber \]
Here, we see that at equilibrium, there are 157.2 molecules of \(D(g)\) for every 1 molecule of \(B(g)\)
Now that we have the ratio of molecules in this reaction, we can construct workable mole fractions.
\(X_D = \frac {157.2}{1 + 157.2}\)
\(X_B = \frac {1}{1 + 157.2}\)
Finally, we can plug everything in to find our partial pressures.
\(P_D = \frac {157.2}{158.2} \times (4.3 \; atm) = 4.27 \; atm\)
\(P_B = \frac {1}{157.8} \times (4.3 \; atm) = 0.027 \; atm\)
Q91
Given the reaction
\[C_3H_5N(g) + 3 \; H_2(g) \leftrightharpoons C_5H_{11}N(g)\nonumber \]
whose equilibrium constant is solved by this equation \[log_{10}(K) = -20.28 + \frac {10.56 \; K}{T}\nonumber \]
- Solve for \(K\) when \(T = 200 \; K\)
- What is partial pressure of \(C_3H_5N(g)\) when \(T = 200 \; K\) and the partial pressure of hydrogen is 1.0 atm and the partial pressure of \( C_5H_{11}N(g)\) is \(2.0 \times 10^{-5}\) atm.
- Solution
-
Part a)
\[log_{10}(K) = -20.28 + \frac {10.56 \; K}{200 \; K}\nonumber \]
\(K = 10^{-20.23} = 5.89 \times 10^{-21}\)
part b)
Set up the equilibrium constant of the reaction, plug in your partial pressures, and solve for \(C_3H_5N(g)\)
\(K = \frac {[C_5H_{11}N]}{[C_5H_5N] \; [H_2]^3}\)
\(K = \frac {2.0 \times 10^{-5}}{[C_5H_5N] \; [1]}\)
\([C_5H_5N] = 3.40 \times 10^{15}\)
Q93
Two equal volume solutions of 2M HCOO- and 2M HCOOH are mixed together. Assume that the volumes are additive. The value of the equilibrium constant Ka for HCOOH is 1.77 x 10-4. What is the ratio between the amounts of HCOOH and HCOO- in the solution at equilibrium?
- Solution
-
The chemical equation for this reaction is
\[HCOOH_{(aq)}+H_{2}O_{l}\leftrightarrow H_{3}O^{+}_{(aq)}+HCOO^{-}_{(aq)}\nonumber \]
This indicates that
\[K_{a}=\frac{[HCOO^{-}][H_{3}O^{+}]}{[HCOOH]}\nonumber \]
Because the volumes are equal and additive, the concentrations of the two solutions become half of what they were initially.
At equilibrium,
\[[HCOO^{-}]=1+x\nonumber \]
\[[H_{3}O^{+}]=x\nonumber \]
\[[HCOOH]=1-x\nonumber \]
Plugging in these values into the equilibrium expression gives
\[1.77\bullet 10^{-4}=\frac{[1+x][x]}{[1-x]}\nonumber \]
Solving the equation for x gives \[x= 1.77\bullet 10^{-4}M\nonumber \]
The ratio of HCOOH and HCOO- is \[\frac{1+x}{1-x}\nonumber \] and due to x being such a small value, the ratio between the amounts of HCOOH and HCOO- is essentially 1.
Q101
The \(∆G_f^o\) of \(\ce{PbO(s)}\) is -188.95 kJ mol-1. Calculate the equilibrium pressure of O2(g) over a sample of pure PbO(s) in contact with pure Pb(s) at 25°C. PbO(s) decomposes according to the equation
\[\ce{PbO_{(s)} <=> Pb (s) + 1/2 O2(g)}\nonumber \]
- Solution
-
Since Gf° for O2(g) and Pbs(s) is 0, for the reaction
\[\Delta G^{\circ}=(0+0)-(-188.95kJ mol^{-1})=188.95kJ mol^{-1}\nonumber \]
The equilibrium constant of the reaction can be computed by
\[ln K= -\frac{\Delta G^{\circ}}{RT}=-76.22\nonumber \]
\[K=7.898\bullet 10^{-34}\nonumber \]
From the chemical equation, we can tell
\[K=(P_{O_{2}})^{1/2}\nonumber \]
Therefore the equilibrium pressure of O2 at 25°C
\[P_{O_{2}}=6.2\bullet 10^{-67}atm\nonumber \]
Q105
If that weren’t enough, Jim’s sister, ., knocked his grass juice (a mixture of 1-Hexanol, \(Cl_{2}\), \(CaCl_{2}\), and cyclohexane) into the family’s benzene-ethanol vat! Assume that the two solvents in the vat are immiscible with each other but are miscible with the grass juice components. Jim separates the benzene and ethanol, and drinks the one with the greater amount of 1-Hexanol. Which one does he drink? Which of the two solvents have the highest concentration of the other components of the grass juice?
- Solution
-
There are two immiscible solvents in the family vat. What this means is that they do not mix/ dissolve well in each other. Consequently, when . poured the grass juice into this vat, the solution technically contains two solvents. Evidently, what this means is that each of the solutes (which are the grass juice constituents mentioned in the question) dissolves to a different extent in each solvent. When the question asks which solvent has the greater amount of 1-Hexanol, it is the same as asking does 1-Hexanol dissolve “more” in either benzene or ethanol (the two solvents). The concept of “like dissolves like” is very important here, and to solve this problem first benzene must be identified as non-polar and driven by dispersion forces, while ethanol is polar. Since polar solvents dissolve polar solutes, then ethanol should be able to dissolve \(CaCl_{2}\) and 1-Hexanol, both polar solutes, much better, while benzene can dissolve \(Cl_{2}\) and cyclohexane, which are nonpolar, to a greater extent. The aptitude that each solvent has in dissolving the solutes directly correlate to the concentrations of solutes that are present in the solvent.
Thus, Jim would drink the ethanol, since it has the highest concentration of the polar 1-Hexanol. Also, the benzene would have the highest concentration of \(Cl_{2}\) and cyclohexane, and the ethanol would also have the highest concentration of \(CaCl_{2}\), which is ionic and therefore “very polar”.
Abstract: “Like dissolves Like”: polar solvents dissolve polar solutes, and nonpolar solvents dissolve polar solutes
Q107
Calculate the pH of a 0.5 M \(H_3PO_4\) acid solution given that \(K_{a1}=7.1 \times 10^{-3}\), \(K_{a2}=6.3 \times 10^{-8}\) and \(K_{a3}=4.2 \times 10^{-13}\).
- Solution
-
A14.107V2
1.25
H14.107V2
Review on how to calculate the pH of a polyprotic acids here.
S14.107V2
\[7.1 \times 10^{-3}=\dfrac{x^2}{(0.5-x)}\nonumber \]
\[x=0.0561\;M=[H^+]\nonumber \]
\[pH=-\log[H^+]=1.25\nonumber \]
We assume that all of the \(H^+\) in solution comes from the dissociation of the first H+ because the second and the third is too small to have a significant effect in the pH of the solution.
Q107
The Haber-Bosch process is a method invented in the 20th century as a method for hydrogen fixation. It is widely used in industry today, and involves reacting nitrogen and hydrogen in the following manner:
\[\ce{N2 (g) + 3H2 (g) \rightleftharpoons 2 NH3 (g)}\nonumber \]
Calculate \(\Delta{G_{rxn}^{\circ}}\). If the pressure of the products and reaction are all kept constant at the same value, in which direction will the reaction go?
Relevant information:
\(\Delta{G_f^{\circ}}\; NH_{2\, (g)} = 199.83\dfrac{kJ}{mol}\)
- Solution
-
The process of calculating \(\Delta{G}\) should be very familiar after reading Q15, so this solution will not elaborate much on this method. With that being said, the \(\Delta{G_{rxn}^{\circ}}\) is as follows:
\(\Delta{G_{rxn}^{\circ}} = 399.66\dfrac{kJ}{mol}\)
Both \(N_{2}\) and \(H_{2}\) have respective \(\Delta{G_{f}}\) of zero. Now, remember that if \(\Delta{G_{rxn}^{\circ}}\) is negative (\(\Delta{G_{rxn}^{\circ}}\)<0), then the reaction is spontaneous in the direction mentioned. However, in this case the \(\Delta{G_{rxn}^{\circ}}\) is definitely NOT less than zero, so it is not spontaneous in the direction \(N_{2\, (g)} + 3H_{2\, (g)} \rightarrow 2 NH_{3\, (g)}\). However, if the chemical formula is "flipped" so that it goes from \(N_{2\, (g)} + 3H_{2\, (g)} \leftarrow 2 NH_{3\, (g)}\), Hess's law states that the corresponding \(\Delta{G_{rxn}^{\circ}}\) is also "flipped" from positive to negative (or vice versa, depending on the value. For this situation, however, the \(\Delta{G_{rxn}^{\circ}}\) does turn negative). What information can be drawn from this is that, since a negative \(\Delta{G_{rxn}^{\circ}}\) means that the reaction will be spontaneous, then it can be inferred that the reaction will favor going from \(N_{2\, (g)} + 3H_{2\, (g)} \leftarrow 2 NH_{3\, (g)}\), rather than \(N_{2\, (g)} + 3H_{2\, (g)} \rightarrow 2 NH_{3\, (g)}\). Without even having to calculate the equilibrium constant, from this information alone, it can be inferred that, at equilibrium, the reactants are favored over the products. Therefore, if both gasses are kept at constant pressure, the reaction will tend to increase concentration of reactants. Thus, the reaction will go left.
Abstract: Find the \(\Delta{G_{rxn}^{\circ}}\), understand what implications it has in regards to equilibrium, and apply this knowledge to infer that the reaction will favor the reactants.
Q109
At 273 K, the equation: H2(g) + I2(g) → 2HI(g) has an equilibrium constant of 60.2
- Solve for ΔGº at 273 K
- How does G change when the pressure of HI is 2 atm, I2 is 4 atm and H2 is 6 atm?
- Is this reaction spontaneous?
- Solution
-
a) ΔG° = -RT ln(K)
ΔG° = -(8.3145 J/K mol)(273 K) ln(60.2)
ΔG° = -9301.1 J/mol
b) ΔG = ΔG° + RT ln(Q)
ΔG = -9301.1 J/mol + (8.3145 J/K mol)(273 K) ln(PHI / PH2PI2)
ΔG = -9301.1 J/mol + (8.3145 J/K mol)(273 K) ln(2 / (6x4))
ΔG = -14941.49 J/mol.
c) This reaction proceeds spontaneously in the forward direction.
Q109
At 773 K the equilibrium constant for the Haber-Bosch process is 1.45x10-5. The chemical reaction involved in the Haber-Bosch process is:
\[ N_{2\, (g)} + 3H_{2\, (g)} \rightleftharpoons 2NH_{3\: (g)} \nonumber \]
- What is \(\Delta G°(773) \) for this reaction?
- What is \(\Delta G \) at 773 K for transforming 1 mole of N2 and 3 moles H2 held at 30 atm to 2 moles of NH3 held at 1 atm?
- In which direction would the previous reaction run spontaneously?
- Solution
-
a. The value of \(\Delta G°(773) \) can be found using the equation \(\Delta G° = -RT \ln K \) where T and K are already known to be 773 K and 1.45x10-5 respectively while R=8.134 J K-1 mol-1.
\[ \Delta G°= -8.314\; J\; K^{-1}\; mol^{-1} \times 773K \times ln(1.45 \times 10^{-5}) = 70052\; J \nonumber \]
\[\Delta G°= 70052\; J \nonumber \]
b. The equation needed to determine \(\Delta G\) is \( \Delta G = RTln(Q/K) \). The values of R, T, and K are known while Q is
\[Q = \dfrac{P_{NH_{3}}^{2}/P_{ref}} {(P_{N_{2}}/P_{ref})(P_{H_{2}}^{3}/P_{ref})} \nonumber \]
Pref =1 atm and the other pressures are stated in the question. So to find Q, the pressures have to be plugged into the equation
\[Q = \dfrac{(1)^{2}} {(20)(20)^{3}} = \dfrac{1}{160000} = 6.25 \times 10^{-6}\nonumber \]
Now that the value of Q is known, \(\Delta G \) can be found
\[ \Delta G= -8.314\; J\; K^{-1}\; mol^{-1} \times 773K \times ln(\frac{6.25 \times 10^{-6}}{1.45 \times 10^{-5}}) = -5291\; J \nonumber \]
\[ \Delta G = -5291\; J \nonumber \]
c. The previous reaction would run towards the products spontaneously because \(\Delta G < 0 \).
Q111
The following reaction is exothermic
\[\ce{SnO2(s) + 2H2(g) → Sn(g) + 2H2O(l)} \nonumber\]
- What is the equilibrium expression based on this chemical equation?
- What happens to the reaction if more H2 is added? SnO2 is added into the system?
- What effect would an increase in temperature have on the system?
- What affect would an increase in pressure have on the system?
- Solution
-
- Add texts here. Do not delete this text first.K = [Sn] / [H2] This is because solids are not included in the equilibrium expression
- If H2 were added, the reaction would shift right, towards the products, more Sn is produced. If SnO2 were added, there would be no effect on the equilibrium because SnO2 is not involve in the equilibrium process (K).
- The reaction would shift towards the reactants. The reaction is exothermic, so heat is treated like a product.
- An increase in pressure would shift the reaction towards the side that has less mole of gas. Therefore, in this reaction, an increased in pressure would shift the reaction to the right, more products are produced. Q111
Q112
Given the chemical reaction
\[\ce{ SnO2(s) \rightleftharpoons Sn (s) + O2 (g)} \nonumber \]
- Formulate the equilibrium expression using activities
- State the effect on \(p\ce{O2}\) at equilibrium if more \(\ce{SnCl4(l)}\) is added to the system
- State the effect on \(p\ce{O2}\) at equilibrium if more \(\ce{O2(g)}\) is added to the system
- Solution
-
a. The activities of solids and liquids are always equal to 1. The activities of gases are equal to the partial pressure of the gas in bars. Therefore the equilibrium expression would be
\[ K = P_{O_{2}} \nonumber \]
b. \(P_{O_{2}} \) would not change because the activity of a liquid is always 1 meaning it has no effect on the equilibrium constant
c. \(P_{O_{2}} \) would decrease because the extra gas would push the system out of equilibrium and in order for the system to return to equilibrium, some of the O2 gas would have to react with some of the Sn(s). This would decrease the amount of O2(g) present in the system and therefore decrease the the pressure of O2(g).
Q113
Arrange the following solutions in order of most acidic to basic: NaOH, NaCN, H2SO4, NH4NO3, NaCl
- Solution
-
\[\ce{H2SO4 > NH4NO3 > NaCl > NaCN > NaOH }\]
Review acids bases here.
- H2SO4 is a strong acid.
- NH4NO3 is formed by a weak base (NH4OH) and a strong acid (HNO3). Hence, NH4NO3 is acidic.
- NaCl is formed by a strong base (NaOH) and a strong acid (HCl). Hence, it is a neutral salt.
- NaCN is formed by a strong base (NaOH) and a weak acid (HCN). Hence, NaCN is basic.
- NaOH is a strong base.
Q115
Given that the \(K_b\) values for \(\ce{NH_3}\) and \(\ce{NH_2NH_2}\) are \(1.8 \times 10^{-5}\) and \(8.5 \times 10^{-7}\), respectively. Which is the stronger acid?
- Solution
-
\(\ce{NH2NH2}\)
Calculate the \(K_a\) values first. Review on how to identify the strength of an acid from its \(K_a\) value here.
For NH3,
\[K_a= \dfrac{1.0 \times 10^{-14}}{1.8 \times 10^{-5}} = 5.56 \times 10^{-10}\nonumber \]
For NH2NH2,
\[K_a= \dfrac{(1.0 \times 10^{-14}}{8.5 \times 10^{-7}}= 1.18 \times 10^{-8}\nonumber \]
Since the Ka value of NH2NH2 is larger, NH2NH2 is the stronger acid.
Q119
Calculate the pH of the following solutions.
- 0.5 M \(\ce{NaCN}\) (\(K_a \text{ of } \ce{HCN}=6.2 \times 10^{-10}\))
- 0.01 M \(\ce{NH4Cl}\) (\(K_b \text{ of } \ce{NH3} = 1.8 \times 10^{-5}\))
- Solution
- 11.5 5.63
Ka=(1*10-14)/(1.8*10-5)=5.56*10-10
5.56*10-10=x2/(0.01-x)
x=2.36*10-6
pH= -log(x)= 5.63H14.119V2
Review on the properties of salts here.
\[\ce{CN- (aq) + H2O (l) <=> HCN (aq) + OH- (aq)}\]
Kb=(1*10-14)/(6.2*10-10)=1.62*10-5
\[ 1.62 \times 10^{-5} =\dfrac{x^2}{0.5-x}\]
x=0.00283
pOH= -log(x)= 2.55
pH= 14-pOH= 11.5
\[\ce{NH4^{+}(aq) + H2O (l) <=>NH3 (aq) + H3O^{+} (aq)}\]
Q131
Identify the stronger acid in each of the following combination. Explain.
- HF and HBr
- H2SO4 and H2SO3
- HOCl and HOBr
- Solution
-
14.131V2
HBr H2SO4 HOCl - Study the effect of structure on acids and bases.
- S14.131V2
-
- HBr is the stronger acid because Br less electronegative and therefore less polar as compared to HF.
- H2SO4 is the stronger acid because as the number of attached oxygen on the O-H bonds increases, the less polar the molecule is.
- For oxyacids, the less polar oxyacids are the ones that are more electronegative. Since Cl is more electronegative than Br, HOCl is the stronger acid.
Q137
Identify the Lewis acid and Lewis base for each of the following reaction.
- \(\ce{H^{+} (aq) + NH3 (aq) <=> NH4^{+} (aq)}\)
- \(\ce{Al^{3+} (aq) + 6H2O (l) <=> Al(H2O)6^{3+} (aq)}\)
- \(\ce{CO2 (g) + H2O (l) <=> H2CO3 (aq)}\)
- Solution
-
Lewis acid
Lewis base
1.
H+ NH3
2.
Al3+
H2O
3.
CO2
H2O
H14.137V2
Study the concept of electron pairs here.
S14.137V2
H+ is the electron-pair acceptor while NH3 is the electron-pair donor. Al3+ is the electron-pair acceptor while H2O is the electron-pair donor. CO2 is the electron-pair acceptor while H2O is the electron-pair donor.
Q139
Beryllium hydroxide is an amphoteric compound. It can react as an acid as well as a base. Please write the reactions of Be(OH)2 and describe its role base on Brønsted-Lowry and Lewis theories.
- Solution
-
Be(OH)2(s)+2H+(aq)-> Be2+(aq)+2H2O(l) (Brønsted-Lowry base, 2H+ acceptor)
Be(OH)2(s)+2OH-(aq)-> Be(OH)42-(aq) (Lewis acid, electron pair acceptor)
H14.139.2P
Consider Brønsted-Lowry and Lewis theories.