1.6: Molecules as Energy Carriers and Converters
- Page ID
- 96609
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Make sure you thoroughly understand the following essential concepts:
- Describe the sources of potential energy and kinetic energy contained in a molecule.
- Describe the nature of "thermal" energy, and how it relates to other forms of kinetic energy and to temperature.
- Explain why the simplest molecules (monatomic and diatomic) have smaller heat capacities than polyatomic molecules.
- Similarly, explain why the dependence of heat capacity on the temperature is different for monatomic and polyatomic molecules.
All molecules at temperatures above absolute zero possess thermal energy— the randomized kinetic energy associated with the various motions the molecules as a whole, and also the atoms within them, can undergo. Polyatomic molecules also possess potential energy in the form of chemical bonds. Molecules are thus both vehicles for storing and transporting energy, and the means of converting it from one form to another when the formation, breaking, or rearrangement of the chemical bonds within them is accompanied by the uptake or release of heat.
Internal Energy: Potential + Kinetic
Chemical substances are made of atoms, or more generally, of positively charged nuclei surrounded by negatively charged electrons. A molecule such as dihydrogen, H2, is held together by electrostatic attractions mediated by the electrons shared between the two nuclei. The total potential energy of the molecule is the sum of the repulsions between like charges and the attractions between electrons and nuclei:
\[PE_{total} = PE_{electron-electron} + PE_{nucleus-nucleus} + PE_{nucleus-electron} \label{1-1}\]
In other words, the potential energy of a molecule depends on the time-averaged relative locations of its constituent nuclei and electrons. This dependence is expressed by the familiar potential energy curve which serves as an important description of the chemical bond between two atoms.
- Translation refers to movement of an object as a complete unit. Translational motions of molecules in solids or liquids are restricted to very short distances comparable to the dimensions of the molecules themselves, whereas in gases the molecules typically travel hundreds of molecular diameters between collisions. In gaseous hydrogen, for example, the molecules will be moving freely from one location to another; this is called translational motion, and the molecules therefore possess translational kinetic energy \[KE_{trans} = \dfrac{mv^2}{2}\] in which \(v\) stands for the average velocity of the molecules; you may recall from your study of gases that \(v\), and therefore \(KE_{trans}\), depends on the temperature.
In addition to translation, molecules composed of two or more atoms can possess other kinds of motion.
- Because a chemical bond acts as a kind of spring, the two atoms in H2 will have a natural vibrational frequency. In more complicated molecules, many different modes of vibration become possible, and these all contribute a vibrational term \(KE_{vib}\) to the total kinetic energy.
- Finally, a molecule can undergo rotational motions which give rise to a third term \(KE_{rot}\).
Thus the total kinetic energy of a molecule is the sum
\[KE_{total} = KE_{trans} + KE_{vib} + KE_{rot} \label{1-2}\]
The total energy of the molecule (i.e, its internal energy \(U\)) is just the sum of total kinetic and potential energies:
\[U = KE_{total} + PE_{total} \label{1-3}\]
Although Equation \ref{1-3} is simple and straightforward, it cannot take us very far in understanding and predicting the behavior of even one molecule, let alone a large number of them. The reason, of course, is the chaotic and unpredictable nature of molecular motion. Fortunately, the behavior of a large collection of molecules, like that of a large population of people, can be described by statistical methods.
How Molecules "Store" Thermal Energy
As noted previously, the heat capacity of a substance is a measure of how sensitively its temperature is affected by a change in heat content; the greater the heat capacity, the less effect a given flow of heat \(q\) will have on the temperature.
Thermal energy is randomized kinetic energy and temperature is a measure of it.
For monatomic gases, temperature is a measure of the average kinetic energy due to translational motions of molecules. If vibrational or rotational motions are also active (e.g., diatomic gases), these motions will also accept thermal energy and reduce the amount that goes into translational motions. Because the temperature depends only on the latter, the effect of the other kinds of motions will be to reduce the dependence of the internal energy on the temperature, thus raising the heat capacity of a substance.
| monatomic | diatomic | triatomic | |||
|---|---|---|---|---|---|
| \(\ce{He}\) | 20.5 | \(\ce{CO}\) | 29.3 | \(\ce{H2O}\) | 33.5 |
| \(\ce{Ne}\) | 20.5 | \(\ce{N2}\) | 29.5 | \(\ce{D2O}\) | 34.3 |
| \(\ce{Ar}\) | 20.5 | \(\ce{F2}\) | 31.4 | \(\ce{CO2}\) | 37.2 |
| \(\ce{Kr}\) | 20.5 | \(\ce{Cl2}\) | 33.9 | \(\ce{CS2}\) | 45.6 |
Whereas monatomic molecules can only possess translational thermal energy, two additional kinds of motions become possible in polyatomic molecules. A linear molecule has an axis that defines two perpendicular directions in which rotations can occur; each represents an additional degree of freedom, so the two together contribute a total of ½ R to the heat capacity.
\[ C_{trans} = \underbrace{\dfrac{1}{2} R}_{\text{x dimension}} + \underbrace{\dfrac{1}{2} R}_{\text{y dimension}} + \underbrace{\dfrac{1}{2} R}_{\text{z dimension}} = \underbrace{\dfrac{3}{2} R}_{\text{translation in 3D}} \label{eq3D}\]
Vibrational and rotational motions are not possible for monatomic species such as the noble gas elements, so these substances have the lowest heat capacities. Moreover, as you can see in the leftmost column of Table \(\PageIndex{1}\), their heat capacities are all the same. This reflects the fact that translational motions are the same for all particles; all such motions can be resolved into three directions in space, each contributing one degree of freedom to the molecule and \(½ R\) to its heat capacity (Equation \ref{eq3D}) where \(R\) is the gas constant, \(8.314\, J \,K^{–1}\).
Think of a "degree of freedom" as a motion that contributes to the total kinetic energy of a molecule.
For a non-linear molecule, rotations are possible along all three directions of space, so these molecules have a rotational heat capacity of \(3/2 R\).
\[ \underbrace{C_{rot}}_{\text{nonlinear molecules}}= \underbrace{\dfrac{1}{2} R}_{\text{x rotation}} + \underbrace{\dfrac{1}{2} R}_{\text{y rotation}} + \underbrace{\dfrac{1}{2} R}_{\text{z rotation}} = \dfrac{3}{2} R \label{eq10} \]
Linear molecules can only rotate in two dimensions so rotational motions in linear molecules contribute less than rotational motions in nonlinear molecules to the heat capacity.
\[ \underbrace{C_{rot}}_{\text{linear molecules}} = \underbrace{\dfrac{1}{2} R}_{\text{x rotation}} + \underbrace{\dfrac{1}{2} R}_{\text{y rotation}} = R \label{eq11} \]
Finally, the individual atoms within a molecule can move relative to each other, producing a vibrational motion. A nonlinear molecule consisting of \(N\) atoms can vibrate in \(3N –6\) different ways or modes, while a linear molecule has \(3N-5\) modes. Each vibrational mode contributes \(R\) (rather than ½ R) to the total heat capacity (these results come from advanced mechanics and will not be proven here).
\[ \underbrace{C_{vib}}_{\text{linear molecules}} = \overbrace{(3N-5)}^{\text{vib degrees of freedom}} R \label{eq12}\]
and
\[ \underbrace{C_{vib}}_{\text{nonlinear molecules}} = \overbrace{(3N-6)}^{\text{vib degrees of freedom}} R \label{eq13}\]
The total heat capacity of a mole of gas molecules is then
\[ C_p = C_{trans} + C_{rot} + C_{vib} \]
which differs based on the geometry and number of atoms in the molecule considered (Equations \ref{eq10} - \ref{eq13}) as shown in Table \(\PageIndex{2}\).
| type of motion → | translation |
Rotation |
vibration |
|---|---|---|---|
| monatomic | \(3/2R\) | \(0\) | \(0\) |
| diatomic | \(3/2 R\) | \(R\) | \(R\) (\(N=2\) in Equation \ref{eq12}) |
| polyatomic | \(3/2 R\) | \(3/2 R\)(nonlinear) or \(R\) (linear) | \((3N – 6)R\) (nonlinear) or \((3N – 5)R\) (linear) |
| separation between adjacent levels, (kJ mol–1) | 6.0 × 10–17 J (O2) | 373 J (HCl) | 26,000 J (HCl) |
Now we are in a position to understand why more complicated molecules have higher heat capacities. The total kinetic energy of a molecule is the sum of those due to the various kinds of motions:
\[KE_{total} = KE_{trans} + KE_{rot} + KE_{vib} \label{2-1}\]
When a monatomic gas absorbs heat, all of the energy ends up in translational motion, and thus goes to increase its temperature. In a polyatomic gas, by contrast, the absorbed energy is partitioned among the other kinds of motions; since only the translational motions contribute to the temperature, the temperature rise is smaller, and thus the heat capacity is larger. There is one very significant complication, however: classical mechanics predicts that the energy is always partitioned equally between all degrees of freedom. Experiments, however, show that this is observed only at quite high temperatures. The reason is that these motions are all quantized. This means that only certain increments of energy are possible for each mode of motion, and unless a certain minimum amount of energy is available, a given mode will not be active at all and will contribute nothing to the heat capacity.
Translational Energy Levels are Effectively Continuous
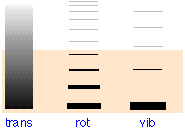
The shading in Figure \(\PageIndex{1}\) indicates the average thermal energy available at 300 K. Only those levels within this range will have significant occupancy as indicated by the thickness of the lines in the two rightmost columns. At 300 K, only the lowest vibrational states and the first few rotational states will be active. Most of the thermal energy will be confined to the translational levels whose minute spacing (10–17 J) causes them to appear as a continuum although technically quantized (by the particle in a box quantum model).
Heat capacity of dihydrogen as a function of temperature. Figure \(\PageIndex{2}\) is typical of those for other polyatomic molecules, and shows the practical consequences of the spacings of the various forms of thermal energy. Thus translational motions are available at virtually all temperatures, but contributions to heat capacity by rotational or vibrational motions can only develop at temperatures sufficiently large to excite these motions.
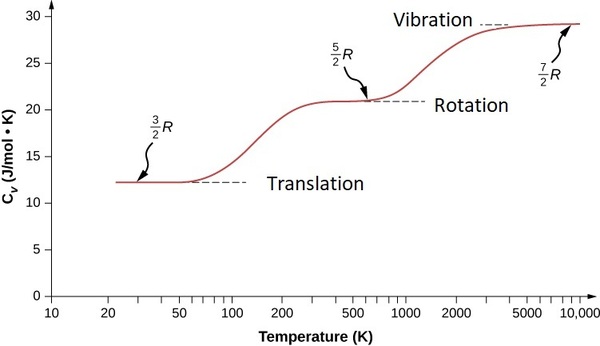
It turns out that translational energy levels are spaced so closely that these motions are active almost down to absolute zero, so all gases possess a heat capacity of at least 3/2 R at all temperatures. Rotational motions do not get started until intermediate temperatures, typically 300-500K, so within this range heat capacities begin to increase with temperature. Finally, at very high temperatures, vibrations begin to make a significant contribution to the heat capacity
The strong intermolecular forces of liquids and many solids allow heat to be channeled into vibrational motions involving more than a single molecule, further increasing heat capacities. One of the well known “anomalous” properties of liquid water is its high heat capacity (75 J mol–1 K–1) due to intermolecular hydrogen bonding, which is directly responsible for the moderating influence of large bodies of water on coastal climates.
Metallic solids are a rather special case. In metals, the atoms oscillate about their equilibrium positions in a rather uniform way which is essentially the same for all metals, so they should all have about the same heat capacity. We can model the atoms of a solid as attached to neighboring atoms by springs (Figure \(\PageIndex{3}\)).
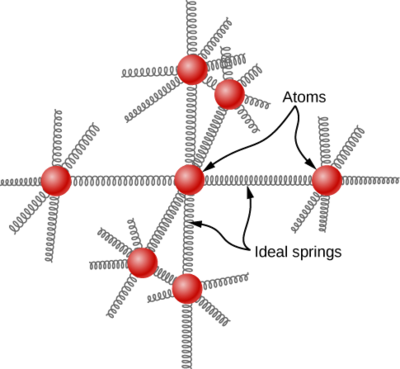
Analogously to the discussion of vibration in the previous module, each atom has six degrees of freedom: one kinetic and one potential for each of the x-, y-, and z-directions. Accordingly, the molar specific heat of a metal should be \(3R\). This result, known as the Law of Dulong and Petit, works fairly well experimentally at room temperature. In the 19th century these workers discovered that the molar heat capacities of all the metallic elements they studied were around to 25 J mol–1 K–1, which is close to what classical physics predicts for crystalline metals. This observation played an important role in characterizing new elements, for it provided a means of estimating their molar masses by a simple heat capacity measurement.
Contributors and Attributions
Stephen Lower, Professor Emeritus (Simon Fraser U.) Chem1 Virtual Textbook


