5.3: Hybridization of Atomic Orbitals
- Page ID
- 20327
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Hybridization was introduced to explain molecular structure when the valence bond theory failed to correctly predict them. It is experimentally observed that bond angles in organic compounds are close to 109°, 120°, or 180°. According to Valence Shell Electron Pair Repulsion (VSEPR) theory, electron pairs repel each other and the bonds and lone pairs around a central atom are generally separated by the largest possible angles.
In this section, we will use a model called valence bond theory to describe bonding in molecules. In this model, bonds are considered to form from the overlapping of two atomic orbitals on different atoms, each orbital containing a single electron. In looking at simple inorganic molecules such as H2 or HF, our present understanding of s and p atomic orbitals will suffice. In order to explain the bonding in organic molecules, however, we will need to introduce the concept of hybrid orbitals.
Hybrid orbitals: sp3 hybridization and tetrahedral bonding
Now let’s turn to methane, the simplest organic molecule. Recall the valence electron configuration of the central carbon:
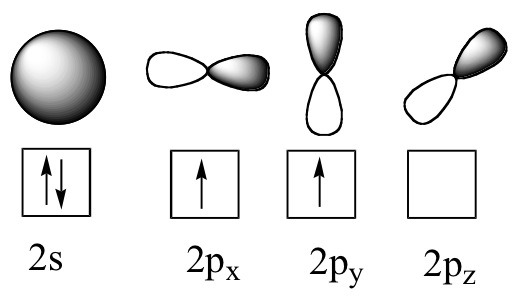
This picture, however, is problematic. How does the carbon form four bonds if it has only two half-filled p orbitals available for bonding? A hint comes from the experimental observation that the four C-H bonds in methane are arranged with tetrahedral geometry about the central carbon, and that each bond has the same length and strength. In order to explain this observation, valence bond theory relies on a concept called orbital hybridization. In this picture, the four valence orbitals of the carbon (one 2s and three 2p orbitals) combine mathematically (remember: orbitals are described by equations) to form four equivalent hybrid orbitals, which are named sp3 orbitals because they are formed from mixing one s and three p orbitals. In the new electron configuration, each of the four valence electrons on the carbon occupies a single sp3 orbital.

The sp3 hybrid orbitals, like the p orbitals of which they are partially composed, are oblong in shape, and have two lobes of opposite sign. Unlike the p orbitals, however, the two lobes are of very different size. The larger lobes of the sp3 hybrids are directed towards the four corners of a tetrahedron, meaning that the angle between any two orbitals is 109.5o.
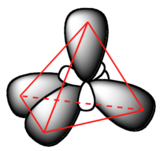
This geometric arrangement makes perfect sense if you consider that it is precisely this angle that allows the four orbitals (and the electrons in them) to be as far apart from each other as possible. This is simply a restatement of the Valence Shell Electron Pair Repulsion (VSEPR) theory that you learned in General Chemistry: electron pairs (in orbitals) will arrange themselves in such a way as to remain as far apart as possible, due to negative-negative electrostatic repulsion.
Each C-H bond in methane, then, can be described as an overlap between a half-filled 1s orbital in a hydrogen atom and the larger lobe of one of the four half-filled sp3 hybrid orbitals in the central carbon. The length of the carbon-hydrogen bonds in methane is 1.09 Å (1.09 x 10-10 m).
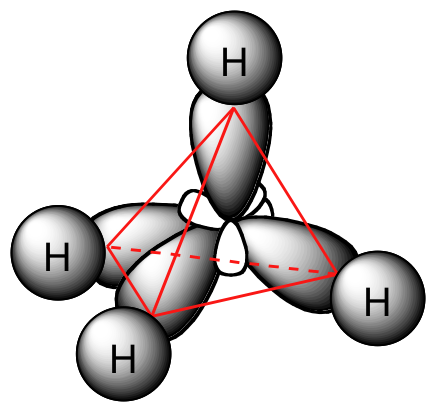
While previously we drew a Lewis structure of methane in two dimensions using lines to denote each covalent bond, we can now draw a more accurate structure in three dimensions, showing the tetrahedral bonding geometry. To do this on a two-dimensional page, though, we need to introduce a new drawing convention: the solid / dashed wedge system. In this convention, a solid wedge simply represents a bond that is meant to be pictured emerging from the plane of the page. A dashed wedge represents a bond that is meant to be pictured pointing into, or behind, the plane of the page. Normal lines imply bonds that lie in the plane of the page.
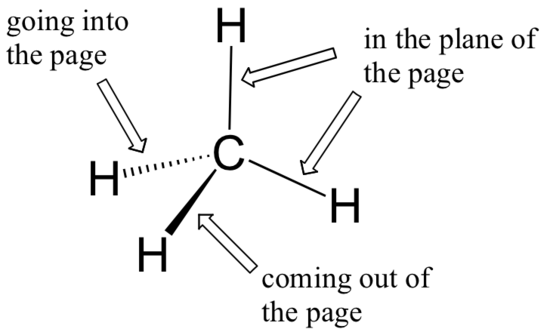
This system takes a little bit of getting used to, but with practice your eye will learn to immediately ‘see’ the third dimension being depicted.
interactive 3D model of the bonding in methane
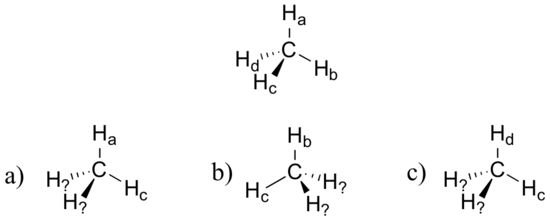
Exercise
Imagine that you could distinguish between the four hydrogens in a methane molecule, and labeled them Ha through Hd. In the images below, the exact same methane molecule is rotated and flipped in various positions. Draw the missing hydrogen atom labels. (It will be much easier to do this if you make a model.)
In the ethane molecule, the bonding picture according to valence orbital theory is very similar to that of methane. Both carbons are sp3-hybridized, meaning that both have four bonds arranged with tetrahedral geometry. The carbon-carbon bond, with a bond length of 1.54 Å, is formed by overlap of one sp3 orbital from each of the carbons, while the six carbon-hydrogen bonds are formed from overlaps between the remaining sp3 orbitals on the two carbons and the 1s orbitals of hydrogen atoms. All of these are sigma bonds.
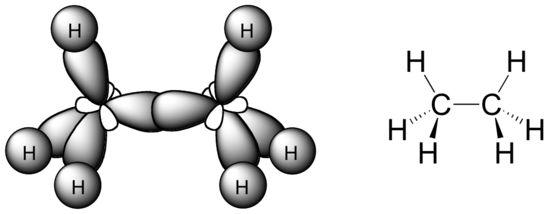
Because they are formed from the end-on-end overlap of two orbitals, sigma bonds are free to rotate. This means, in the case of ethane molecule, that the two methyl (CH3) groups can be pictured as two wheels on a hub, each one able to rotate freely with respect to the other.
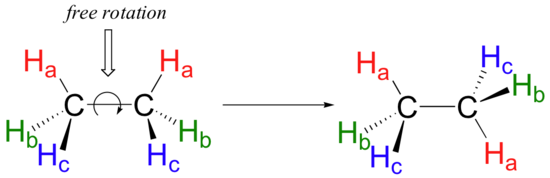
In another module we will learn more about the implications of rotational freedom in sigma bonds, when we discuss the ‘conformation’ of organic molecules.
The sp3 bonding picture is also used to described the bonding in amines, including ammonia, the simplest amine. Just like the carbon atom in methane, the central nitrogen in ammonia is sp3-hybridized. With nitrogen, however, there are five rather than four valence electrons to account for, meaning that three of the four hybrid orbitals are half-filled and available for bonding, while the fourth is fully occupied by a (non-bonding) pair of electrons.

The bonding arrangement here is also tetrahedral: the three N-H bonds of ammonia can be pictured as forming the base of a trigonal pyramid, with the fourth orbital, containing the lone pair, forming the top of the pyramid.
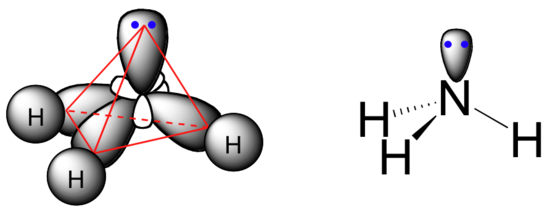
Recall from your study of VSEPR theory in General Chemistry that the lone pair, with its slightly greater repulsive effect, ‘pushes’ the three N-H sigma bonds away from the top of the pyramid, meaning that the H-N-H bond angles are slightly less than tetrahedral, at 107.3˚ rather than 109.5˚.
VSEPR theory also predicts, accurately, that a water molecule is ‘bent’ at an angle of approximately 104.5˚. It would seem logical, then, to describe the bonding in water as occurring through the overlap of sp3-hybrid orbitals on oxygen with 1sorbitals on the two hydrogen atoms. In this model, the two nonbonding lone pairs on oxygen would be located in sp3 orbitals.

Some experimental evidence, however, suggests that the bonding orbitals on the oxygen are actually unhybridized 2p orbitals rather than sp3 hybrids. Although this would seem to imply that the H-O-H bond angle should be 90˚ (remember that p orbitals are oriented perpendicular to one another), it appears that electrostatic repulsion has the effect of distorting this p-orbital angle to 104.5˚. Both the hybrid orbital and the nonhybrid orbital models present reasonable explanations for the observed bonding arrangement in water, so we will not concern ourselves any further with the distinction.
Exercise
Draw, in the same style as the figures above, an orbital picture for the bonding in methylamine.
Formation of pi bonds - sp2 and sp hybridization
The valence bond theory, along with the hybrid orbital concept, does a very good job of describing double-bonded compounds such as ethene. Three experimentally observable characteristics of the ethene molecule need to be accounted for by a bonding model:
- Ethene is a planar (flat) molecule.
- Bond angles in ethene are approximately 120o, and the carbon-carbon bond length is 1.34 Å, significantly shorter than the 1.54 Å single carbon-carbon bond in ethane.
- There is a significant barrier to rotation about the carbon-carbon double bond.
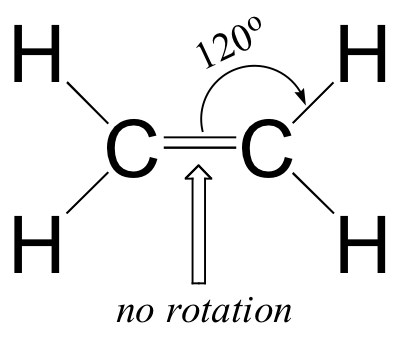
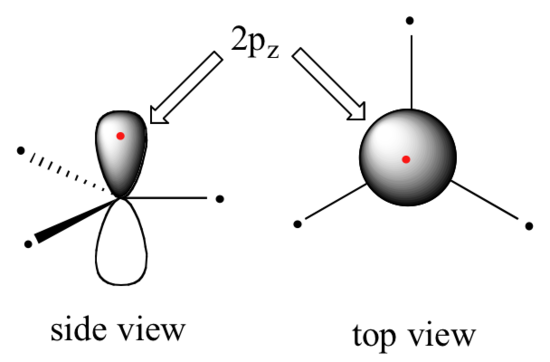
Clearly, these characteristics are not consistent with an sp3 hybrid bonding picture for the two carbon atoms. Instead, the bonding in ethene is described by a model involving the participation of a different kind of hybrid orbital. Three atomic orbitals on each carbon – the 2s, 2px and 2py orbitals – combine to form three sp2 hybrids, leaving the 2pz orbital unhybridized.

The three sp2 hybrids are arranged with trigonal planar geometry, pointing to the three corners of an equilateral triangle, with angles of 120°between them. The unhybridized 2pz orbital is perpendicular to this plane (in the next several figures, sp2 orbitals and the sigma bonds to which they contribute are represented by lines and wedges; only the 2pz orbitals are shown in the 'space-filling' mode).
The carbon-carbon double bond in ethene consists of one sigma bond, formed by the overlap of two sp2 orbitals, and a second bond, called a π (pi) bond, which is formed by the side-by-side overlap of the two unhybridized 2pz orbitals from each carbon.
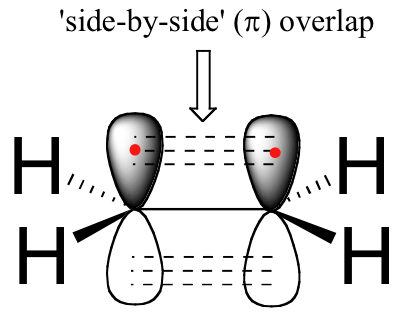
another view
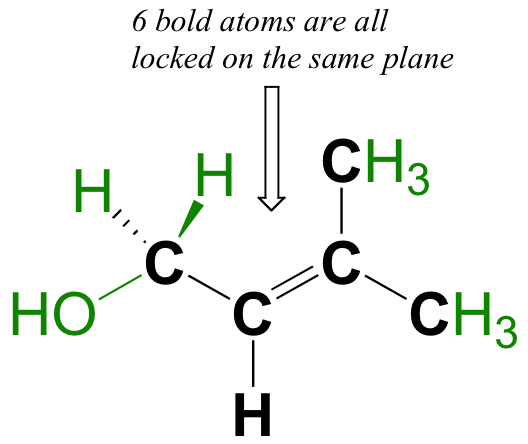
The pi bond does not have symmetrical symmetry. Because they are the result of side-by-side overlap (rather then end-to-end overlap like a sigma bond), pi bonds are not free to rotate. If rotation about this bond were to occur, it would involve disrupting the side-by-side overlap between the two 2pz orbitals that make up the pi bond. The presence of the pi bond thus ‘locks’ the six atoms of ethene into the same plane. This argument extends to larger alkene groups: in each case, the six atoms of the group form a single plane.
Conversely, sigma bonds such as the carbon-carbon single bond in ethane (CH3CH3) exhibit free rotation, and can assume many different conformations, or shapes.
Example
Circle the six atoms in the molecule below that are ‘locked’ into the same plane.
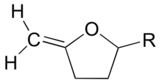
Exercise
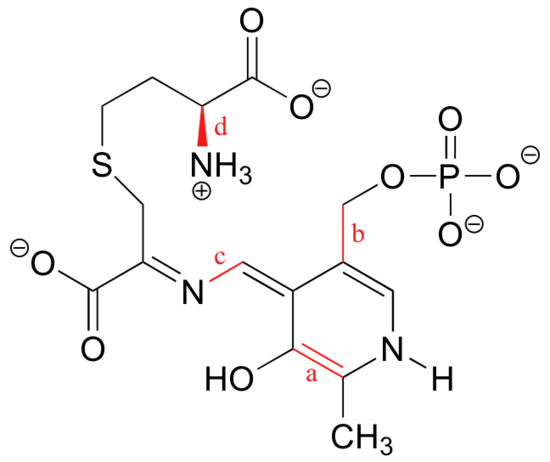
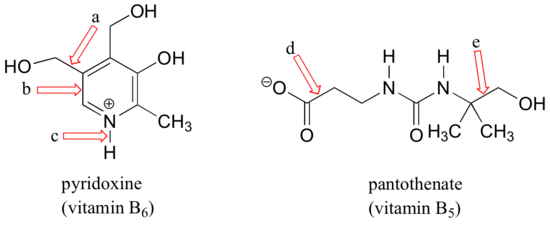
What kinds of orbitals are overlapping in bonds a-d indicated below?
A similar picture can be drawn for the bonding in carbonyl groups, such as formaldehyde. In this molecule, the carbon is sp2-hybridized, and we will assume that the oxygen atom is also sp2 hybridized. The carbon has three sigma bonds: two are formed by overlap between two of its sp2 orbitals with the 1sorbital from each of the hydrogens, and the third sigma bond is formed by overlap between the remaining carbon sp2 orbital and an sp2 orbital on the oxygen. The two lone pairs on oxygen occupy its other two sp2 orbitals.
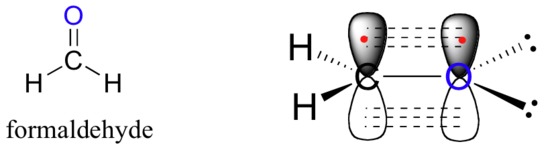
The pi bond is formed by side-by-side overlap of the unhybridized 2pz orbitals on the carbon and the oxygen. Just like in alkenes, the 2pz orbitals that form the pi bond are perpendicular to the plane formed by the sigma bonds.
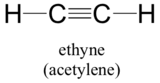
This molecule is linear: all four atoms lie in a straight line. The carbon-carbon triple bond is only 1.20Å long. In the hybrid orbital picture of acetylene, both carbons are sp-hybridized. In an sp-hybridized carbon, the 2s orbital combines with the 2px orbital to form two sp hybrid orbitals that are oriented at an angle of 180°with respect to each other (eg. along the x axis). The 2py and 2pz orbitals remain unhybridized, and are oriented perpendicularly along the y and z axes, respectively.


another view
The C-C sigma bond, then, is formed by the overlap of one sp orbital from each of the carbons, while the two C-H sigma bonds are formed by the overlap of the second sp orbital on each carbon with a 1s orbital on a hydrogen. Each carbon atom still has two half-filled 2py and 2pz orbitals, which are perpendicular both to each other and to the line formed by the sigma bonds. These two perpendicular pairs of p orbitals form two pi bonds between the carbons, resulting in a triple bond overall (one sigma bond plus two pi bonds).

The hybrid orbital concept nicely explains another experimental observation: single bonds adjacent to double and triple bonds are progressively shorter and stronger than ‘normal’ single bonds, such as the one in a simple alkane. The carbon-carbon bond in ethane (structure A below) results from the overlap of two sp3 orbitals.

In alkene B, however, the carbon-carbon single bond is the result of overlap between an sp2 orbital and an sp3 orbital, while in alkyne C the carbon-carbon single bond is the result of overlap between an sp orbital and an sp3 orbital. These are all single bonds, but the bond in molecule C is shorter and stronger than the one in B, which is in turn shorter and stronger than the one in A.
The explanation here is relatively straightforward. An sp orbital is composed of one s orbital and one p orbital, and thus it has 50% s character and 50% p character. sp2 orbitals, by comparison, have 33% s character and 67% p character, while sp3 orbitals have 25% s character and 75% p character. Because of their spherical shape, 2s orbitals are smaller, and hold electrons closer and ‘tighter’ to the nucleus, compared to 2p orbitals. Consequently, bonds involving sp + sp3 overlap (as in alkyne C) are shorter and stronger than bonds involving sp2 + sp3 overlap (as in alkene B). Bonds involving sp3-sp3overlap (as in alkane A) are the longest and weakest of the group, because of the 75% ‘p’ character of the hybrids.
Example
For each of the bonds indicated by arrows a-e in the figures below, describe the bonding picture by completing this sentence:
"The sigma bond indicated by this arrow is formed by the overlap of an ________ orbital of a _________atom and an ________orbital of a _______atom."
Contributors and Attributions
Organic Chemistry With a Biological Emphasis by Tim Soderberg (University of Minnesota, Morris)

