Skip to main content
Chemistry LibreTexts

Chapter 1 Solutions

  1. Last updated
  2. Save as PDF
  • Page ID
    1116

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    In-chapter Exercises

    E1.1: Mass numbers are:

    1. 31P
    2. 32P
    3. 37Cl

    E1.2:

    image002.png

    E1.3:

    image004.png

    E1.4:

    1. a neutral magnesium atom: 1s22s22p63s2
    2. a Mg2+ atom: 1s22s22p6
    3. a neutral potassium atom: 1s22s22p63s23p64s1
    4. a K+ ion: 1s22s22p63s23p6
    5. a Cl- ion: 1s22s22p63s23p6

    E1.5:

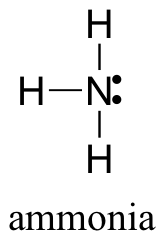
    image006.png

    E1.6:

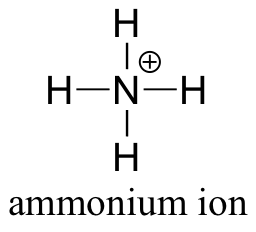
    image008.png

    E1.7:

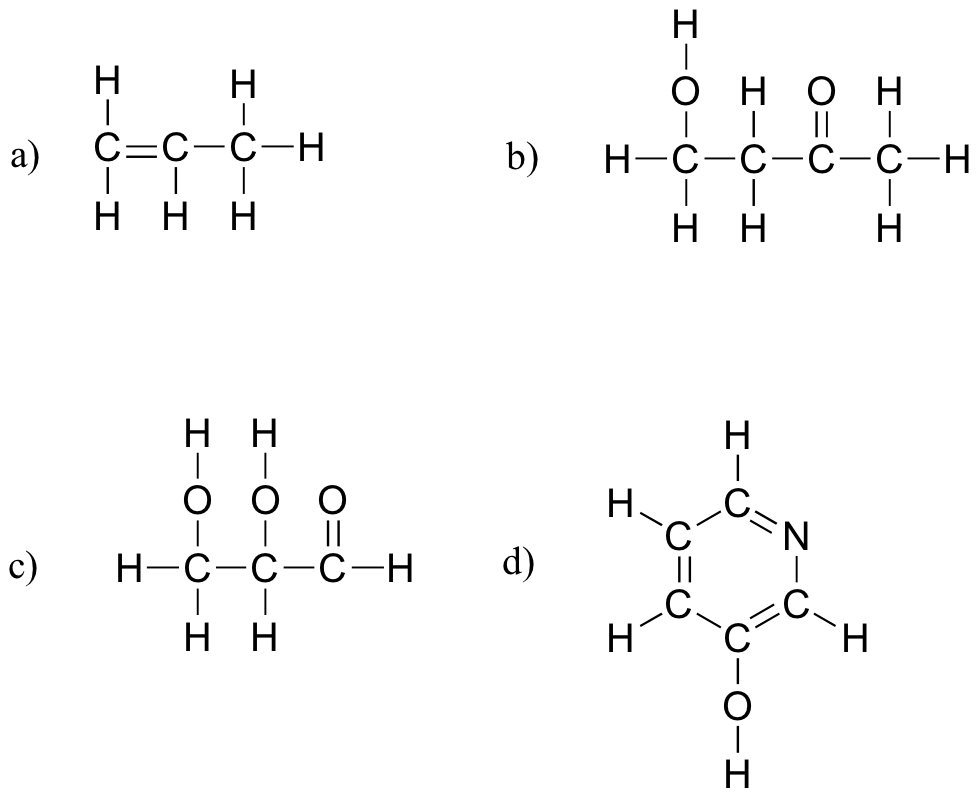
    image010.png

    E1.8:

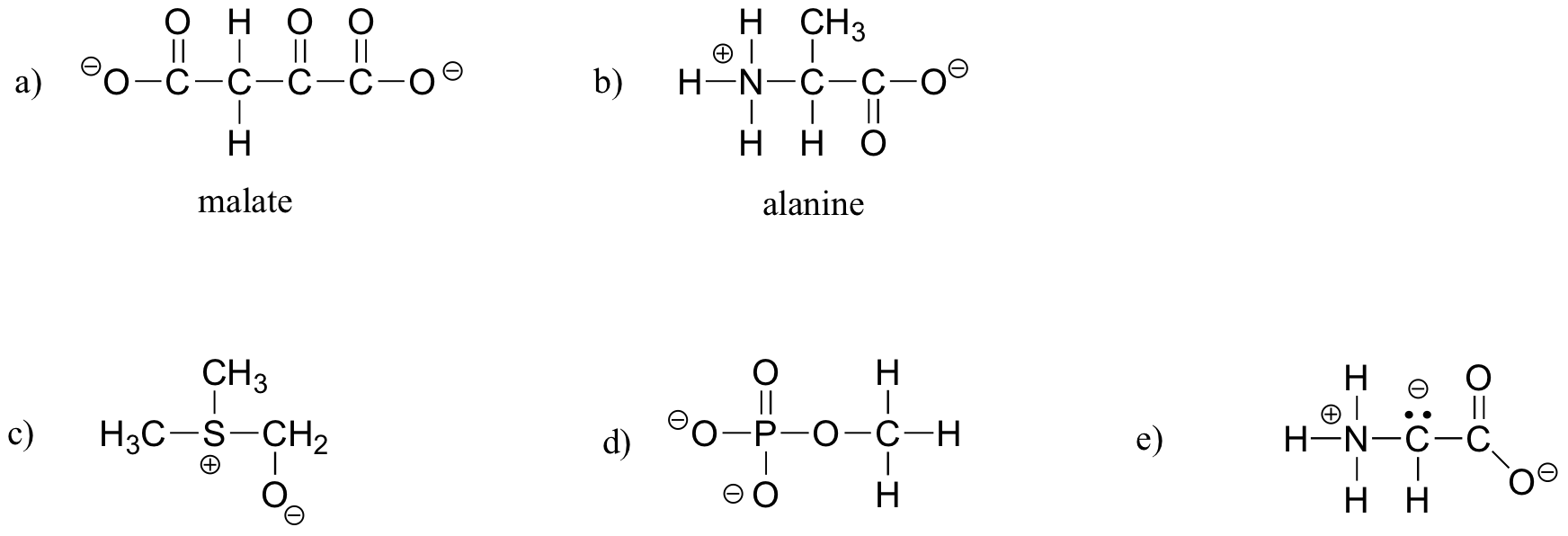
    image012.png

    E1.9:

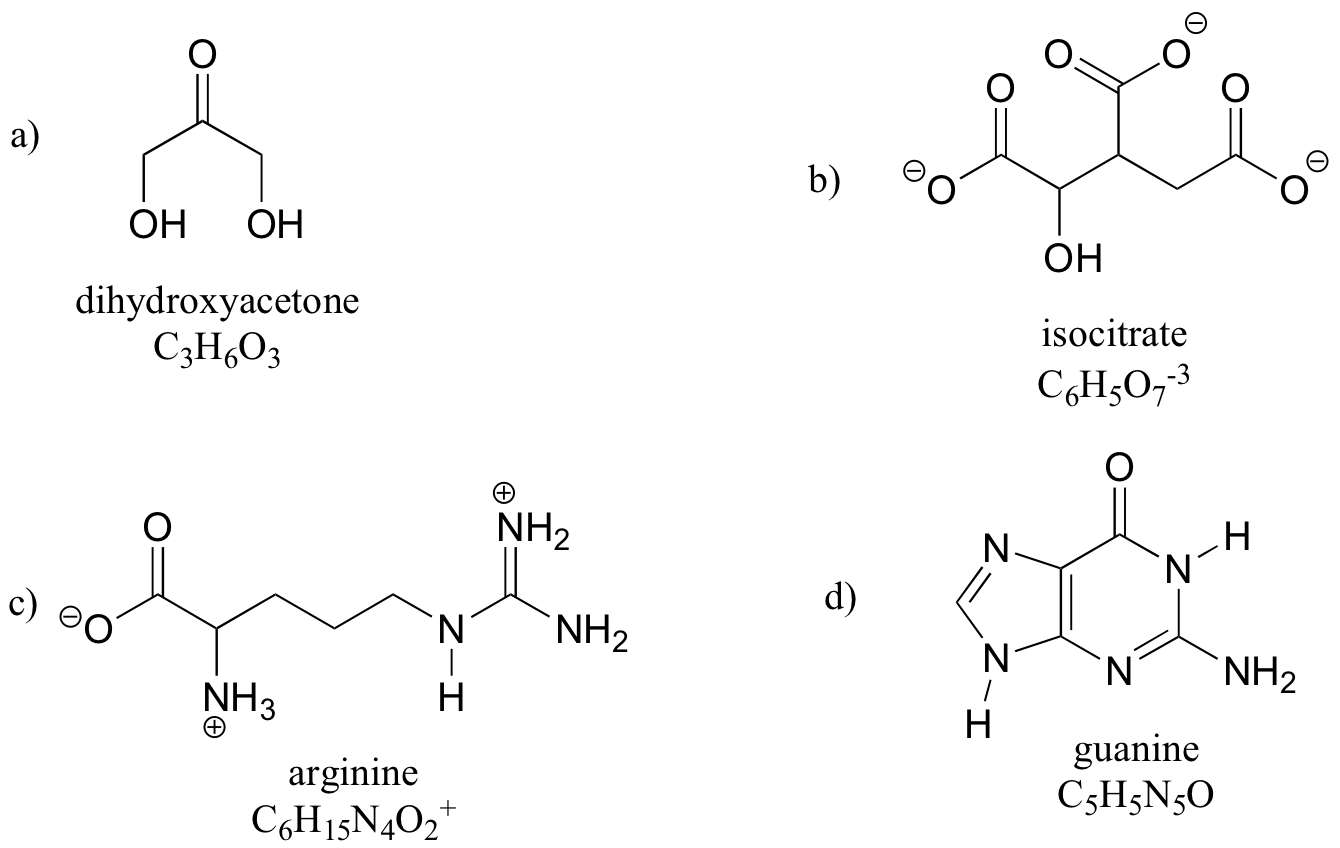
    image014.png

    E1.10:

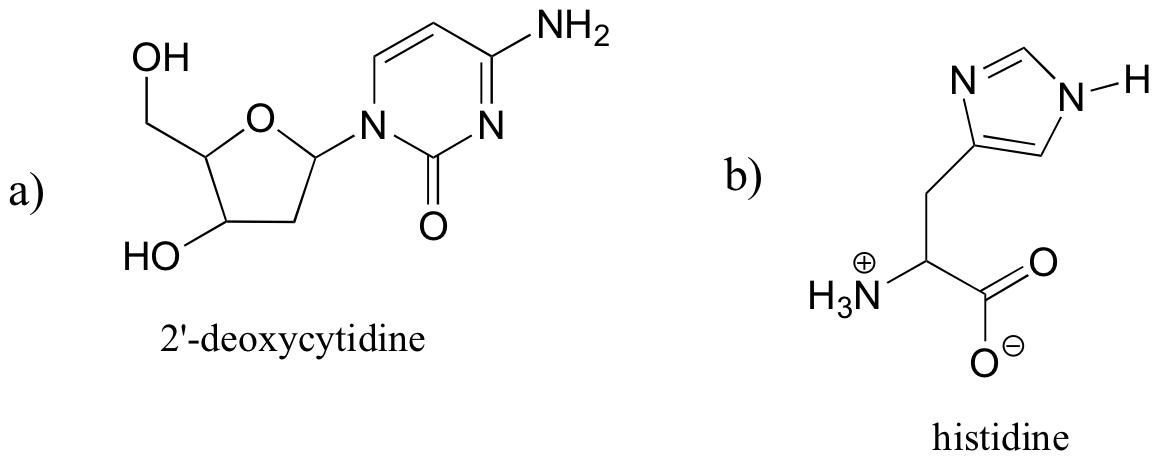
    image016.png

    E1.11:

    a) C5H12

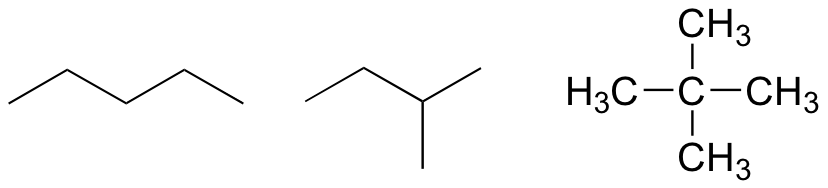
    image018.png

    b) C4H10O

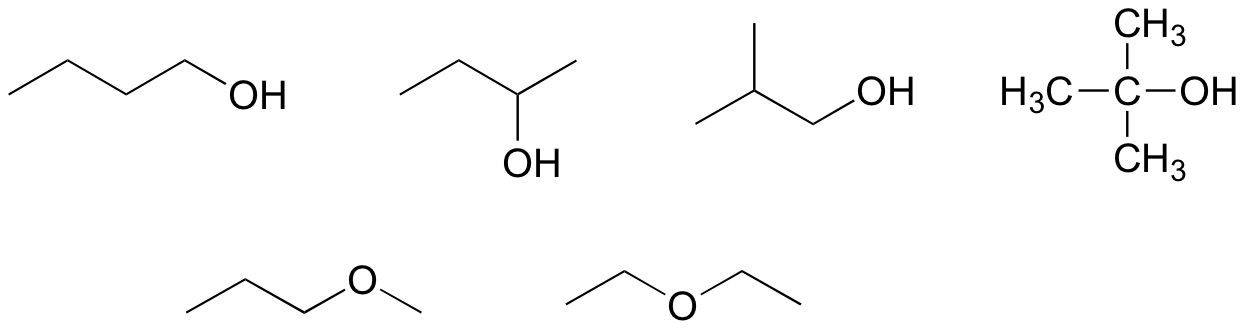
    image020.png

    c) C3H9N

    image022.png

    E1.12:

    1. a) 2-deoxycytidine: IHD = 5 (2 rings, 3 double bonds)
    2. b) histidine: IHD = 4 (2 rings, 2 double bonds)
    3. c) C9H10NOI: IHD = 5
    4. d) an ion with the molecular formula C6H11O7- : IHD = 1

    E1.13:

    1. a) carboxylate, sulfide, aromatic, two amide groups (one of which is cyclic)
    2. b) tertiary alcohol, thioester
    3. c) carboxylate, ketone
    4. d) ether, primary amine, alkene

    E1.14:

    The following molecules (and many others) fit the descriptions in the problem:

    image024.png

    E1.15:

    1. acetic acid: ethanoic acid
    2. chloroform: trichloromethane
    3. acetone: 2-propanone

    E1.16:

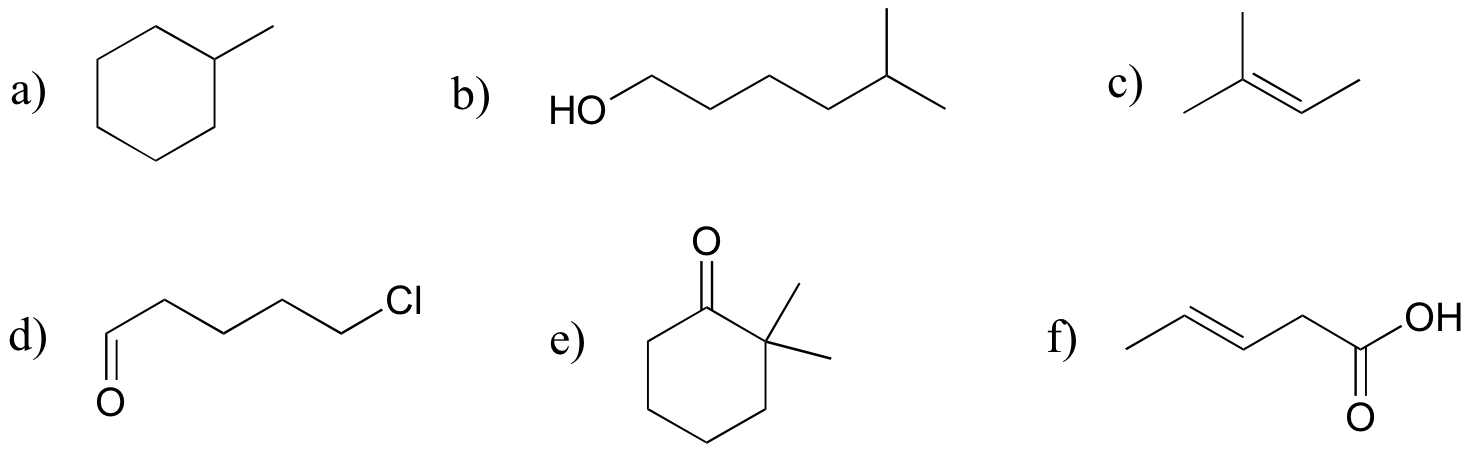
    image026.png

    E1.17:

    image028.png

    E1.18:

    The bonding in chloroform consists of three of the sp3 hybrid orbitals on the central carbon atom overlapping with 3p orbitals on clorine. The fourth bond is an overlap between the fourth sp3 orbital on carbon and the 1s orbital of hydrogen.

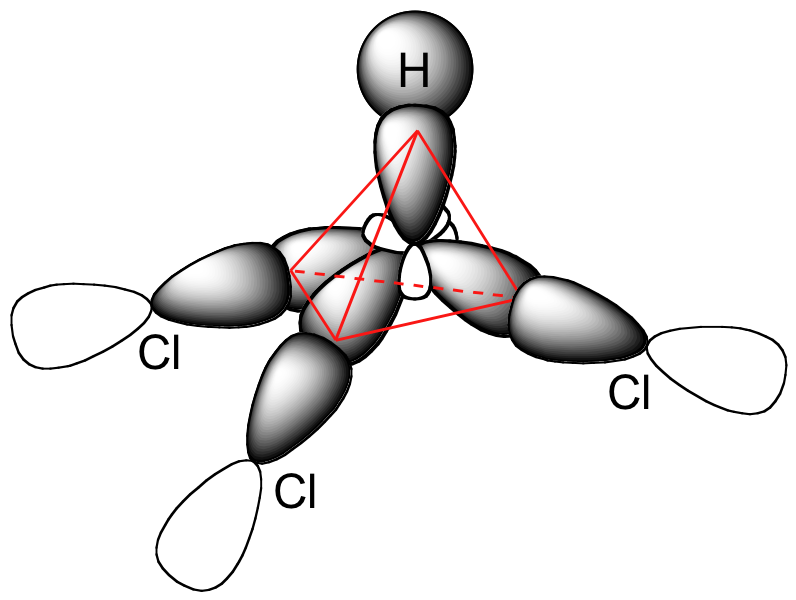
    image030.png

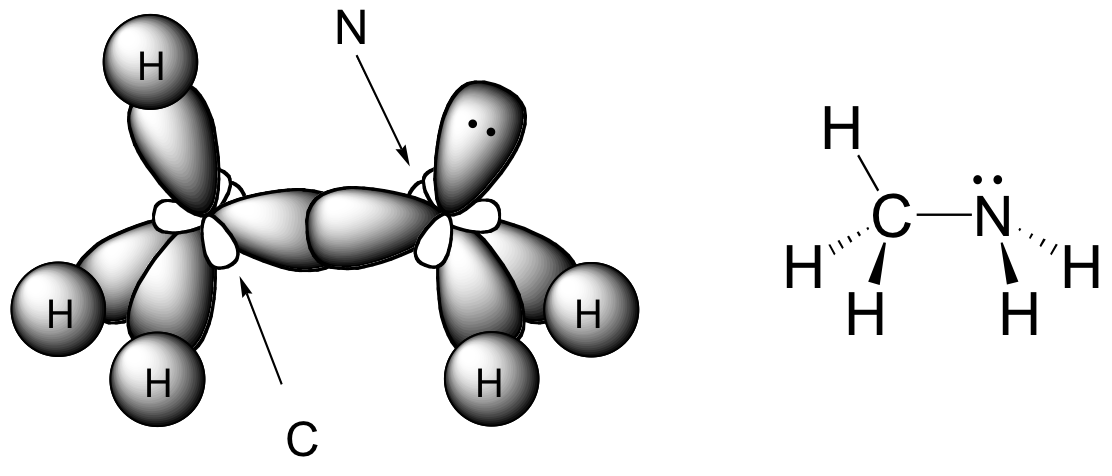
    E1.19:

    Both the carbon and the nitrogen atom in CH3NH2 are sp3-hybridized. The C-N sbond is an overlap between two sp3 orbitals.

    image032.png

    E1.20:

    image034.png

    E1.21:

    1. a) Csp2-Csp2
    2. b) Csp2-Csp3
    3. c) Csp2-Nsp2
    4. d) Csp3-Nsp3

    E1.22:

    The three bonds that are drawn as solid wedges should be drawn as lines – they are all coming out of planar, sp2-hybridized carbons and should be shown lying in the plane of the page.

    E1.23:

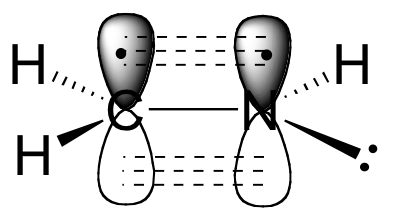
    image036.png

    The carbon and nitrogen atoms are bond sp2-hybridized. The carbon-nitrogen double bond is composed of a s bond formed from two sp2 orbitals, and a pi bond formed from the side-by-side overlap of two unhybridized 2p orbitals.

    E1.24:

    1. The sigma bond indicated by this arrow is formed by the overlap of an sp2 orbital of a carbon atom and an sp3 orbital of a carbon atom.
    2. The sigma bond indicated by this arrow is formed by the overlap of an sp2 orbital of a carbon atom and an sp2 orbital of a carbon atom.
    3. The sigma bond indicated by this arrow is formed by the overlap of an sp2 orbital of a nitrogen atom and an s orbital of a hydrogen atom.
    4. The sigma bond indicated by this arrow is formed by the overlap of an sp2 orbital of a carbon atom and an sp3 orbital of a carbon atom.
    5. The sigma bond indicated by this arrow is formed by the overlap of an sp3 orbital of a carbon atom and an sp3 orbital of a carbon atom.

    End-of-chapter problems

    P1.1:

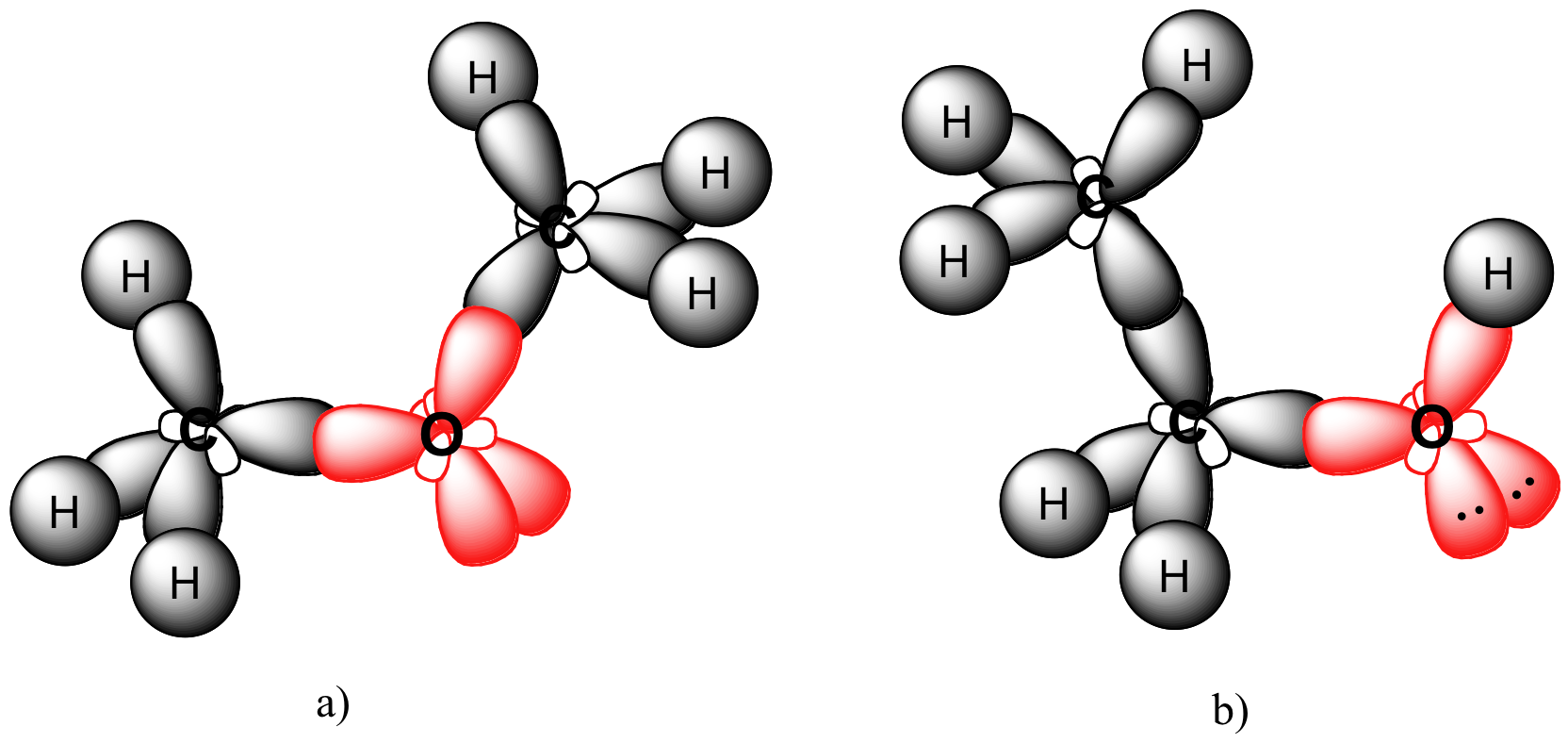
    image038.png

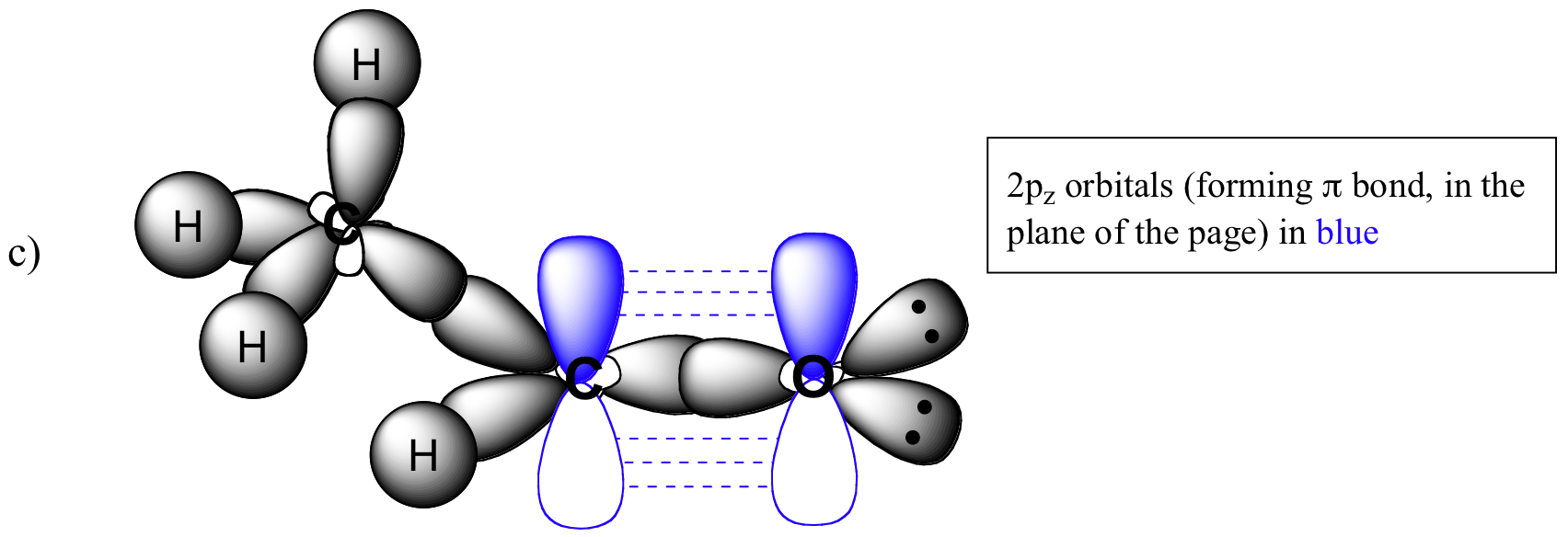
    image040.png

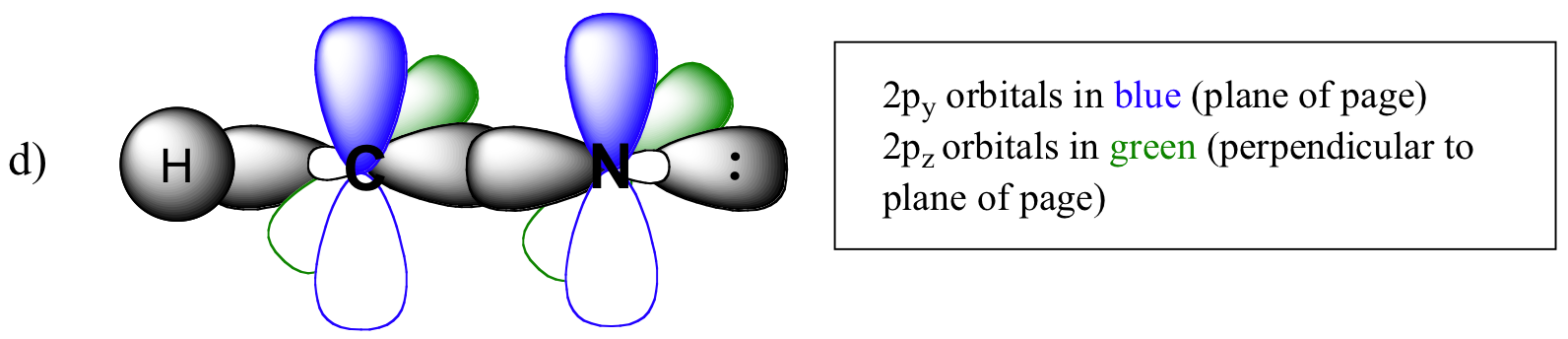
    image042.png

    P1.2:

    1. a lithium cation (Li+): 1s2
    2. a calcium cation (Ca2+): 1s22s12p63s23p6
    3. a iron cation in the ferric (Fe+3) state: 1s22s12p63s23p64s23d3

    P1.3: There are many possible correct answers to this problem – check your answer with your TA or instructor.

    P1.4:

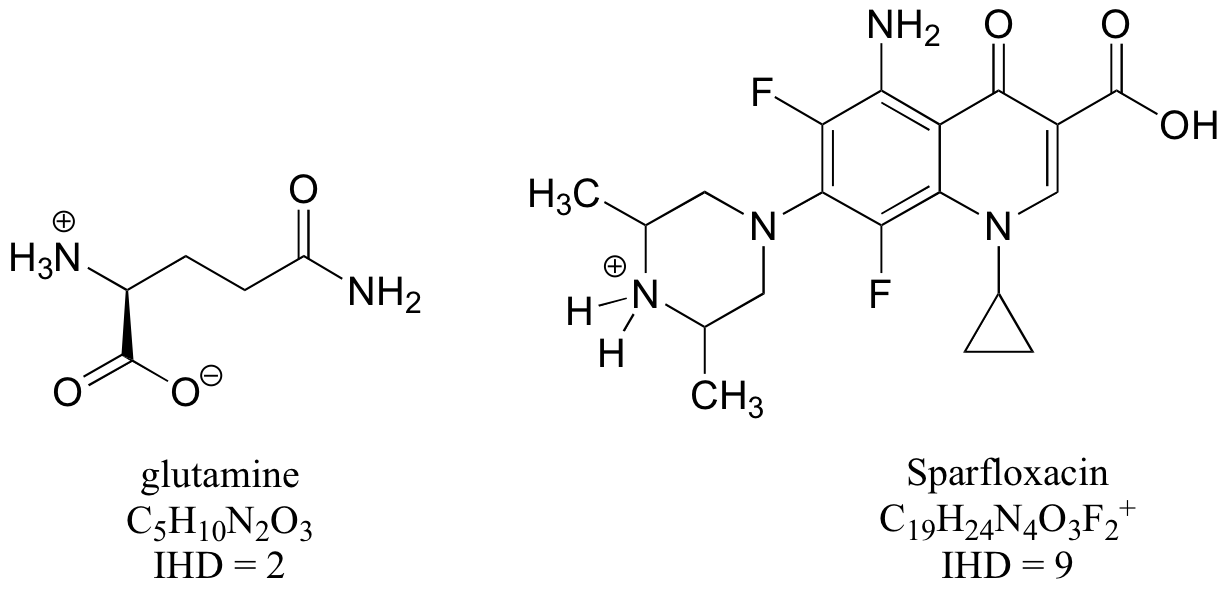
    image044.png

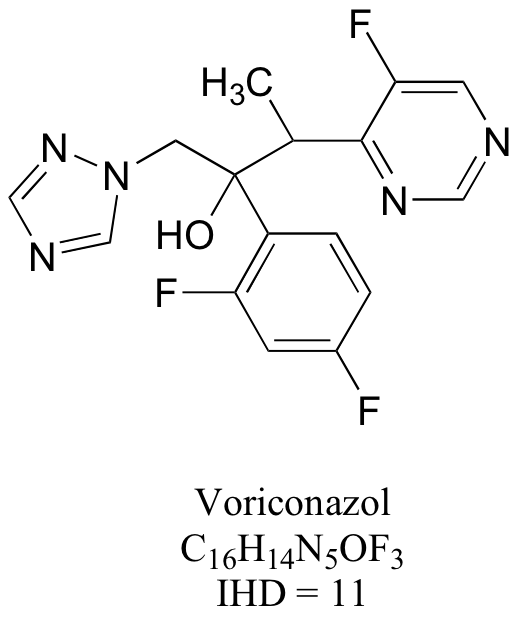
    image046.png

    Notice in doing this problem that it is much easier to determine the IHD from the structure rather than the molecular formula – just count rings and multiple bonds! But it would still be good practice to use the molecular formulas to calculate IHDs, then check that they match what you determined from the structures.

    P1.5:

    a-i; j) see structures below

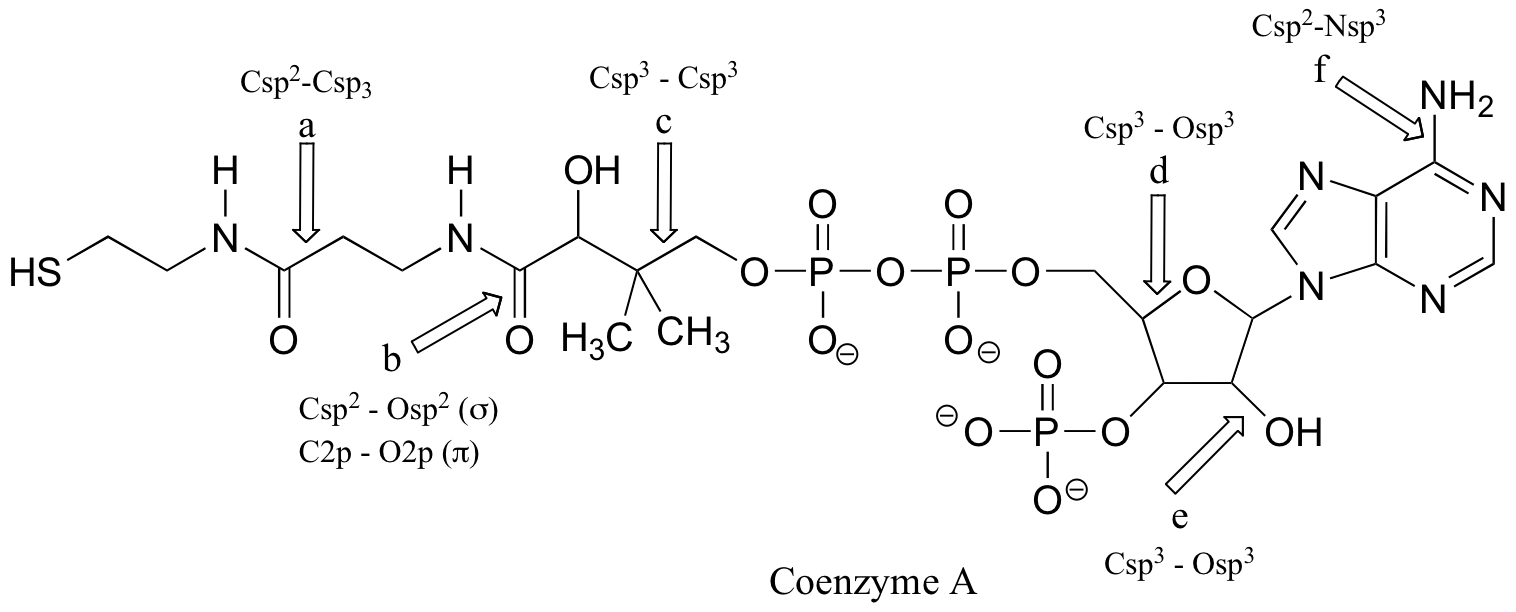
    image048.png

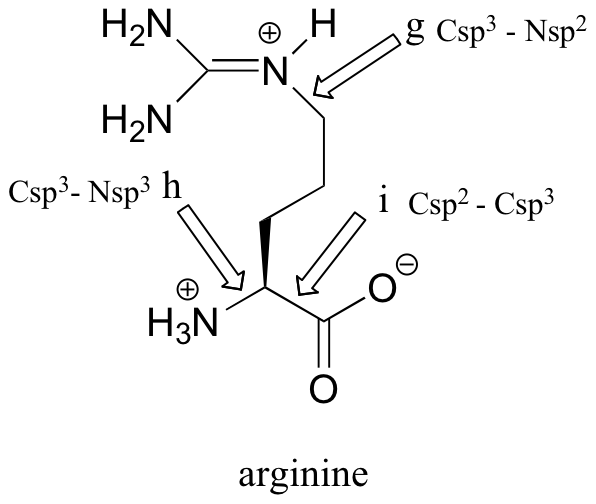
    image050.png

    k) the molecular formula of arginine is C6H15N4O2.

    P1.6:

    a) Csp3 – Osp3

    b) Csp2 – Csp3

    c) Csp2 – Nsp2

    d) Csp2 – Csp2

    e) Csp3 – Csp3

    f) Csp2 – Csp2

    g) Csp3- Csp3

    h)Csp2 – H1s

    i) Csp2 – Osp2

    j) Csp2 – Cl3p

    k) Nsp3 – H1s

    l) Compound 3 contains two aldehydes, compound one contains an ether, compound 2 contains an amide, compound 3 contains a terminal alkene, and compound 4 contains a secondary amine.

    m) The molecular formula of compound 3 is C10H14O2.

    P1.7:

    image052.png

    P1.8:

    image054.png

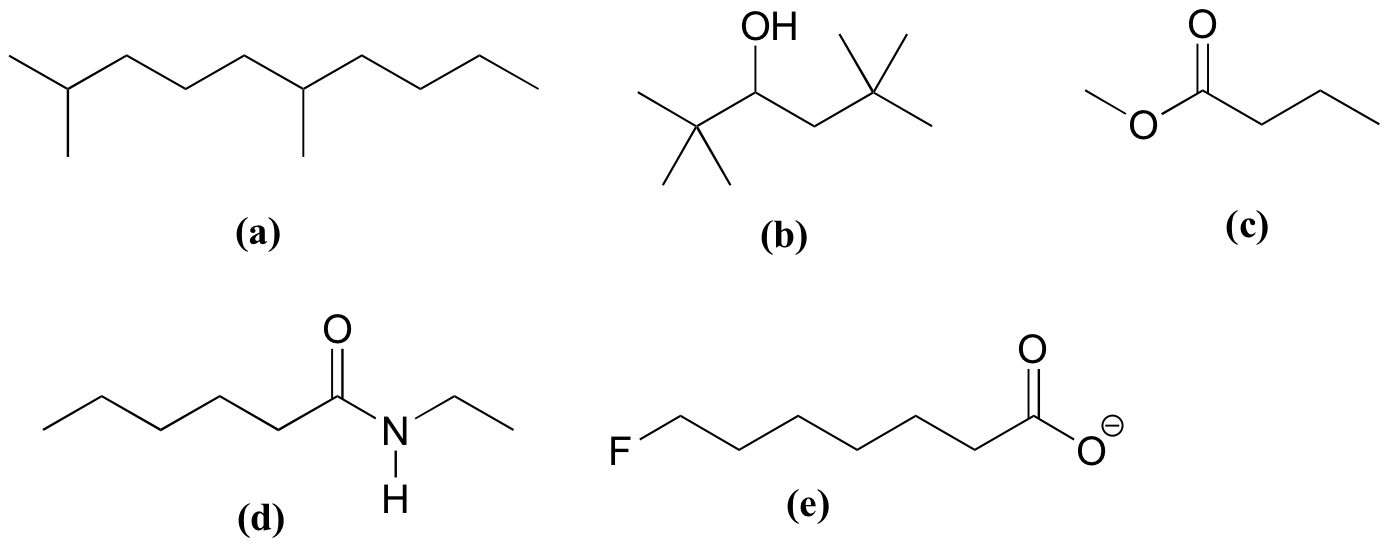
    P1.9: shortest e<c<d<f<b<a longest

    P1.10

    image056.png

    Challenge problems

    C1.1: If the bonds in water were formed from the two half-filled, unhybridized 2p orbitals on oxygen, the bonding geometry would be approximately to 90o, rather than 103.5o as is actually observed. Unhybridized p orbitals lie at right angles to one another!

    C1.2: The bonding an allene can be depicted thus:

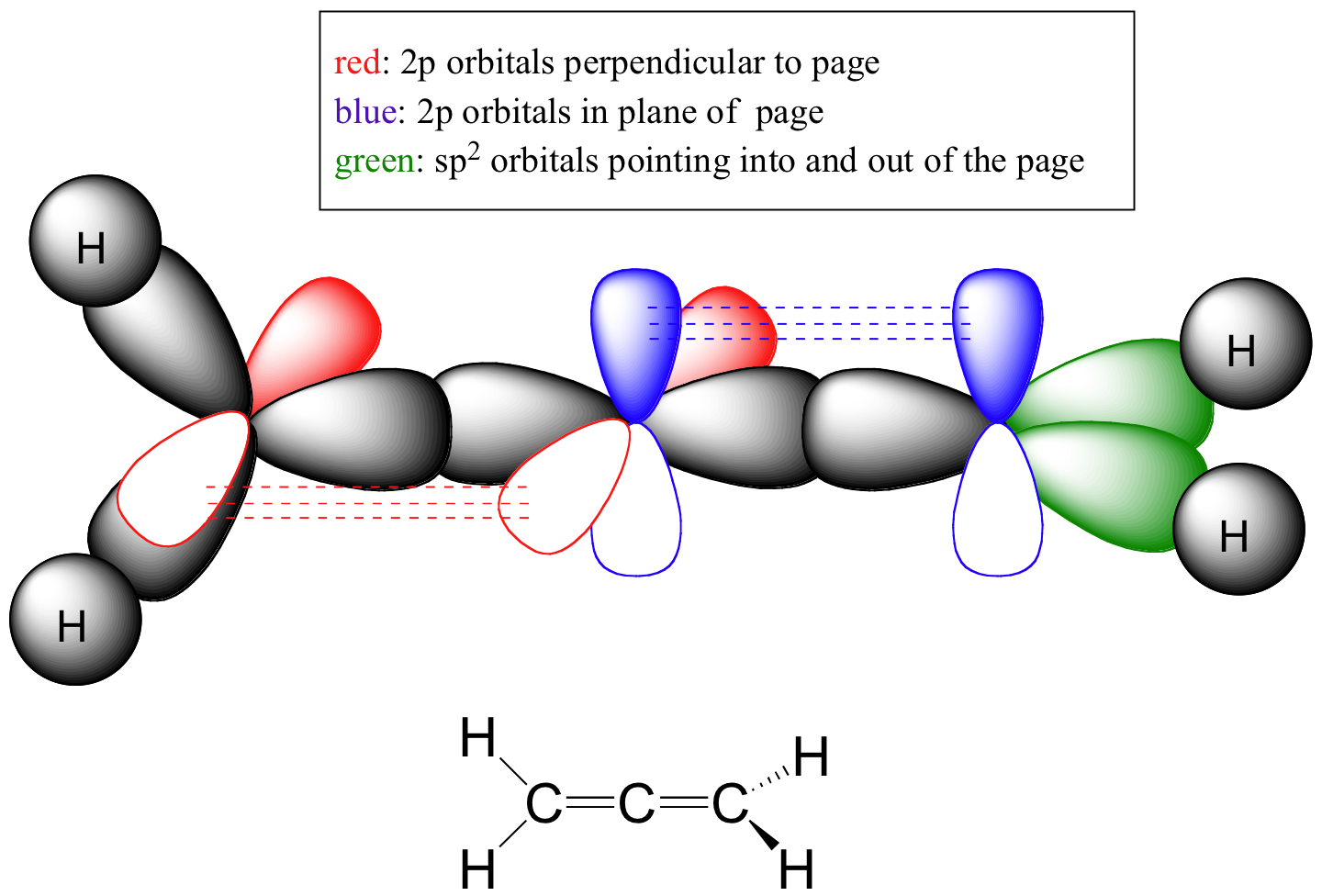
    image058.png

    Notice that the central carbon is sp-hybridized, while the two end carbons are sp2-hybridized: the left one with the three sp2 hybrid orbitals in the plane of the page, the right one with two if the three orbitals pointing into or out of the plane of the page.

    Contributors

    • Organic Chemistry With a Biological Emphasis, Tim Soderberg (University of Minnesota, Morris)

    This page titled Chapter 1 Solutions is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by via source content that was edited to the style and standards of the LibreTexts platform.

    This page titled Chapter 1 Solutions is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Tim Soderberg via source content that was edited to the style and standards of the LibreTexts platform.