7.3: Electron Configurations of Atoms

 

Learning Objectives 

• Using the Aufbau Principle, the Pauli Exclusion Principle, and Hund's rule to predict an atom's electron configuration using the periodic table as a guide 
• Differentiate between (spdf) electron configuration, orbital box diagram, and Nobel Gas Configuration 
• Determine the number of valence electrons in atom based on the electron configuration and main group number 
• Note the exeptions in electron configurations when electrons shift to obtain a half filled orbital or a half filled orbital  

 

Introduction

The electron configuration of an atom is the representation of the arrangement of electrons distributed among the orbital shells and subshells. Commonly, the electron configuration is used to describe the orbitals of an atom in its ground state, but it can also be used to represent an atom that has ionized into a cation or anion by compensating for the loss of or gain of electrons in their subsequent orbitals  (we will examine those in the next section). Many of the physical and chemical properties of elements can be correlated to their unique electron configurations. The valence electrons, electrons in the outermost shell, are the determining factor for the unique chemistry of the element.

 

Recall, we can use the periodic table to rank the energy levels of various orbitals. 

 

Using the periodic table to determine the electron configurations of atoms is key, but also keep in mind that there are certain rules to follow when assigning electrons to different orbitals. The periodic table is an incredibly helpful tool in writing electron configurations. 

Assigning Electron Configuration 

 

We write electronic configurations by following the aufbau principle (from German, meaning “building up”). First we determine the number of electrons in the atom; then we add electrons one at a time to the lowest-energy orbital available without violating the Pauli Exclusion Principle . That is, recognizing that each orbital can hold two electrons, one with spin up ↑, corresponding to m_s = +½, which is arbitrarily written first, and one with spin down ↓, corresponding to m_s = −½. A filled orbital is indicated by ↑↓, in which the electron spins are said to be paired. Here is a schematic orbital box diagram for a hydrogen atom in its ground state:

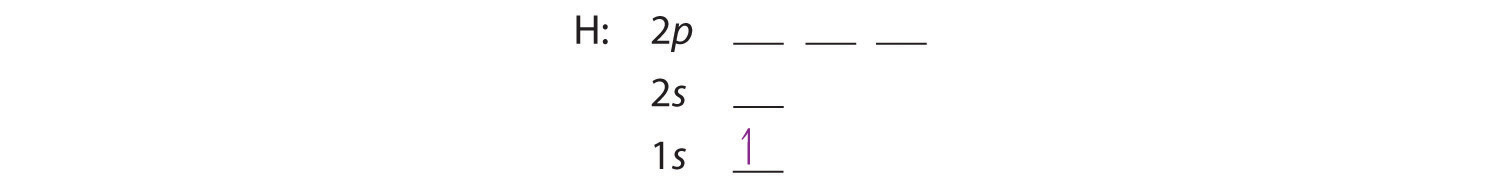
From the orbital diagram, we can write the electron configuration in an abbreviated form in which the occupied orbitals are identified by their principal quantum number n and their value of l (s, p, d, or f), with the number of electrons in the subshell indicated by a superscript. For hydrogen, therefore, the single electron is placed in the 1s orbital, and the electron configuration (also known a spdf notation) is written as 1s¹ and read as “one-s-one.”

A neutral helium atom, with an atomic number of 2 (Z = 2), has two electrons. We place one electron in the orbital that is lowest in energy, the 1s orbital. From the Pauli exclusion principle, we know that an orbital can contain two electrons with opposite spin, so we place the second electron in the same orbital as the first but pointing down, so that the electrons are paired. The orbital diagram for the helium atom is therefore

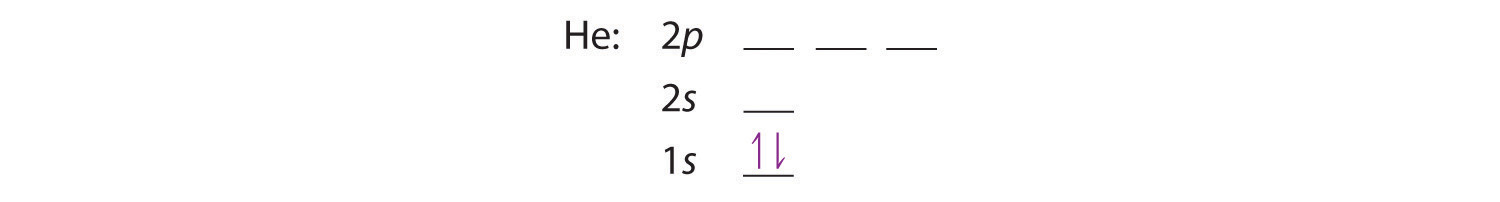
written as 1s², where the superscript 2 implies the pairing of spins. Otherwise, our configuration would violate the Pauli principle.

The next element is lithium, with Z = 3 and three electrons in the neutral atom. We know that the 1s orbital can hold two of the electrons with their spins paired. Figure 6.29 tells us that the next lowest energy orbital is 2s, so the orbital diagram for lithium is

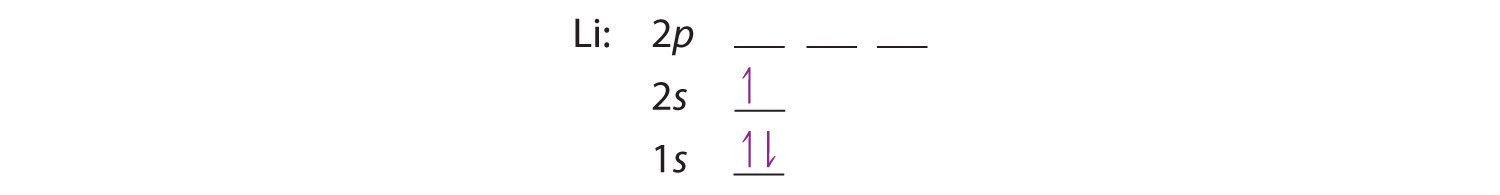
This electron configuration is written as 1s²2s¹.

The next element is beryllium, with Z = 4 and four electrons. We fill both the 1s and 2s orbitals to achieve a 1s²2s² electron configuration:

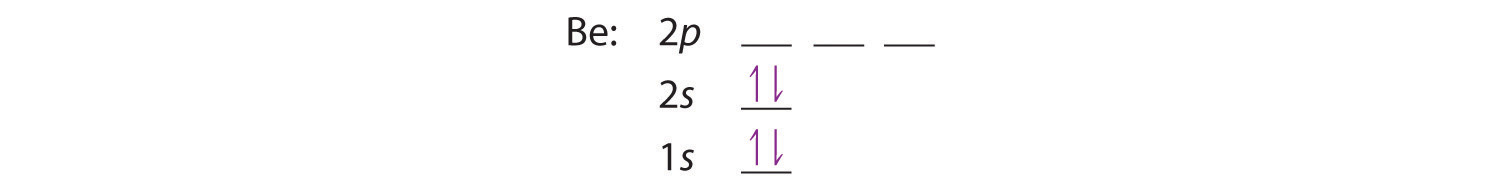
When we reach boron, with Z = 5 and five electrons, we must place the fifth electron in one of the 2p orbitals. Because all three 2p orbitals are degenerate, it doesn’t matter which one we select. The electron configuration of boron is 1s²2s²2p¹:

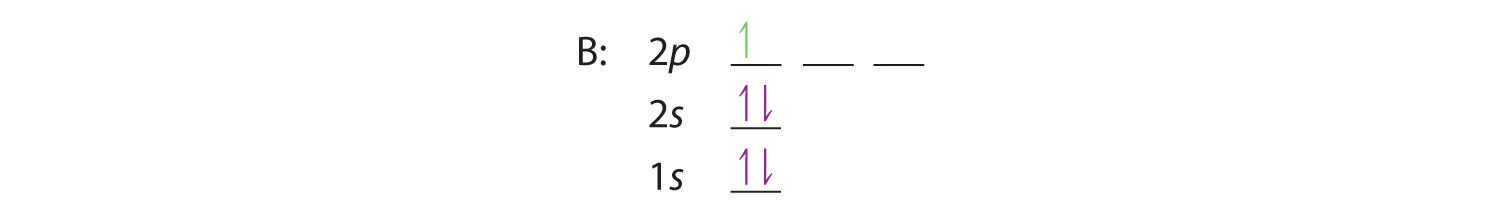
At carbon, with Z = 6 and six electrons, we are faced with a choice. Should the sixth electron be placed in the same 2p orbital that already has an electron, or should it go in one of the empty 2p orbitals? If it goes in an empty 2p orbital, will the sixth electron have its spin aligned with or be opposite to the spin of the fifth? In short, which of the following three orbital diagrams is correct for carbon, remembering that the 2p orbitals are degenerate?

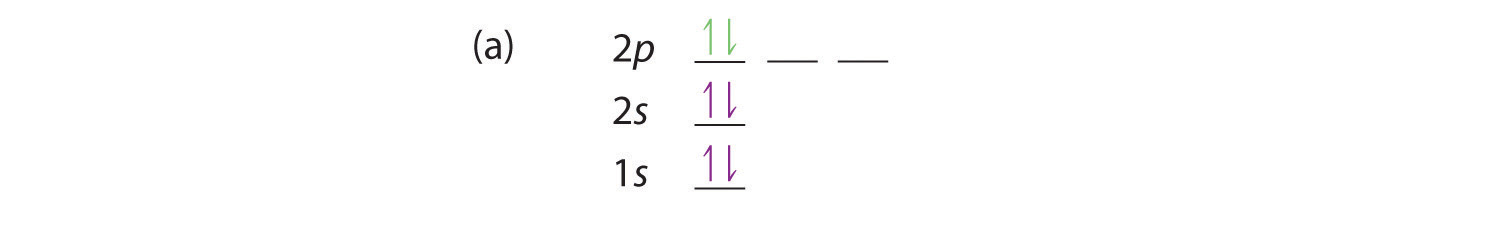
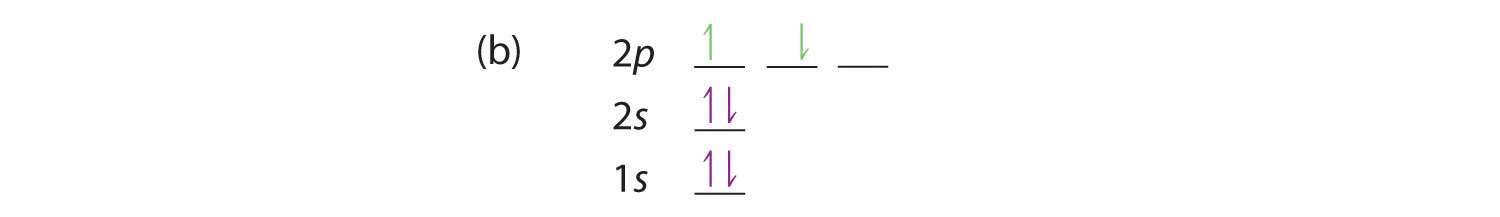
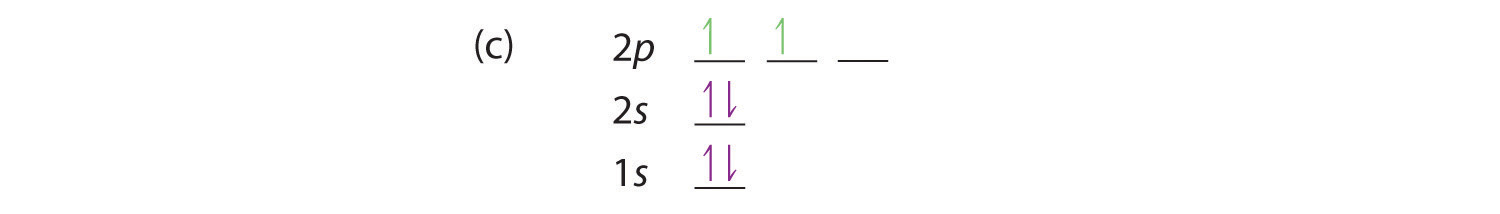
Because of electron-electron repulsions, it is more favorable energetically for an electron to be in an unoccupied orbital than in one that is already occupied; hence we can eliminate choice a. Similarly, experiments have shown that choice b is slightly higher in energy (less stable) than choice c because electrons in degenerate orbitals prefer to line up with their spins parallel; thus, we can eliminate choice b. Choice c illustrates Hund’s rule (named after the German physicist Friedrich H. Hund, 1896–1997), which today says that the lowest-energy electron configuration for an atom is the one that has the maximum number of electrons with parallel spins in degenerate orbitals. By Hund’s rule, the electron configuration of carbon, which is 1s²2s²2p², is understood to correspond to the orbital diagram shown in c. Experimentally, it is found that the ground state of a neutral carbon atom does indeed contain two unpaired electrons.

When we get to nitrogen (Z = 7, with seven electrons), Hund’s rule tells us that the lowest-energy arrangement is

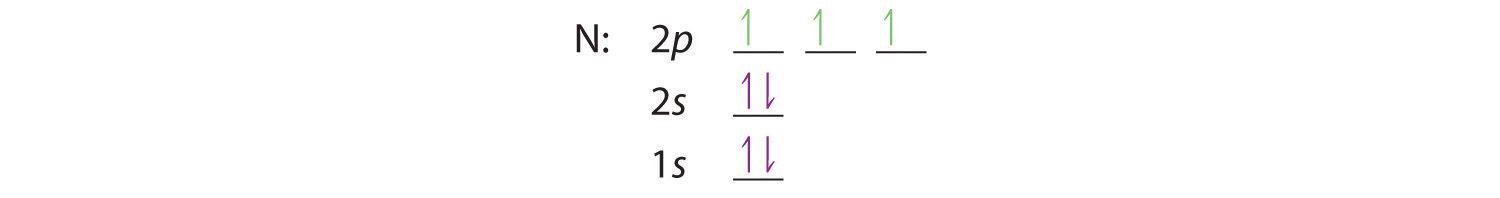
with three unpaired electrons. The electron configuration of nitrogen is thus 1s²2s²2p³.

At oxygen, with Z = 8 and eight electrons, we have no choice. One electron must be paired with another in one of the 2p orbitals, which gives us two unpaired electrons and a 1s²2s²2p⁴ electron configuration. Because all the 2p orbitals are degenerate, it doesn’t matter which one has the pair of electrons.

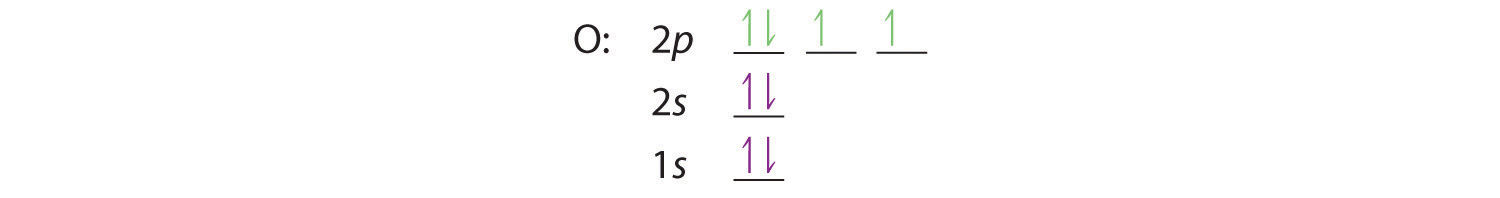
Similarly, fluorine has the electron configuration 1s²2s²2p⁵:

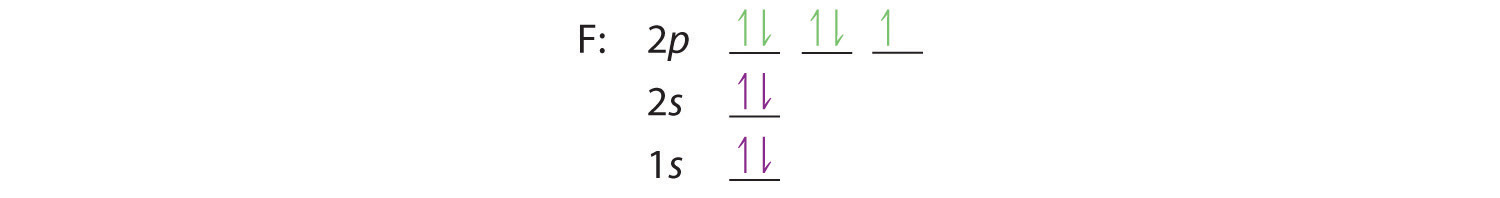
When we reach neon, with Z = 10, we have filled the 2p subshell, giving a 1s²2s²2p⁶ electron configuration:

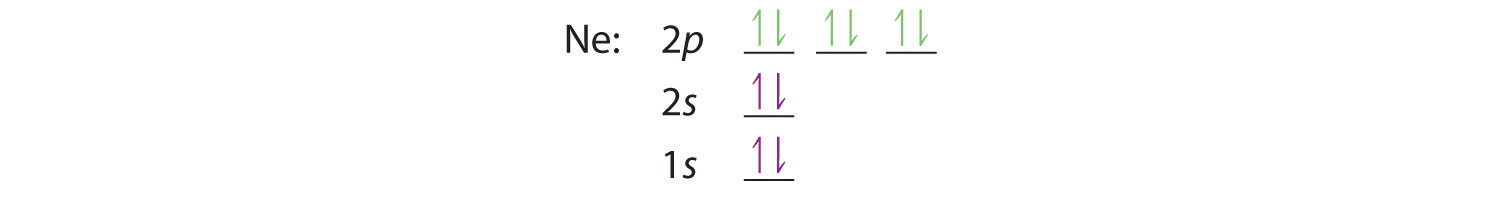
Notice that for neon, as for helium, all the orbitals through the 2p level are completely filled. This fact is very important in dictating both the chemical reactivity and the bonding of helium and neon, as you will see.

 

Let's take a look video tutor to help you understand how to use the periodic table to write electron configuration for atoms in various elements. 

Nobel Gas Configuration 

As we continue through the periodic table in this way, writing the electron configurations of larger and larger atoms, it becomes tedious to keep copying the configurations of the filled inner subshells. In practice, chemists simplify the notation by using a bracketed noble gas symbol to represent the configuration of the noble gas from the preceding row because all the orbitals in a noble gas are filled. For example, [Ne] represents the 1s²2s²2p⁶ electron configuration of neon (Z = 10), so the electron configuration of sodium, with Z = 11, which is 1s²2s²2p⁶3s¹, is written as [Ne]3s¹:

Neon	Z = 10	1s^22s^22p^6
Sodium	Z = 11	1s^22s^22p^63s^1 = [Ne]3s^1

Because electrons in filled inner orbitals are closer to the nucleus and more tightly bound to it, they are rarely involved in chemical reactions. This means that the chemistry of an atom depends mostly on the electrons in its outermost shell (with the greatest "n" value), which are called the valence electrons. The simplified notation allows us to see the valence-electron configuration more easily. Using this notation to compare the electron configurations of sodium and lithium, we have:

Sodium	1s^22s^22p^63s^1 = [Ne]3s^1
Lithium	1s^22s^1 = [He]2s^1

It is readily apparent that both sodium and lithium have one s electron in their valence shell. We would therefore predict that sodium and lithium have very similar chemistry, which is indeed the case. Now we have explained why elements in the same group have similar chemical properties. 

As we continue to build the eight elements of period 3, the 3s and 3p orbitals are filled, one electron at a time. This row concludes with the noble gas argon, which has the electron configuration [Ne]3s²3p⁶, corresponding to a filled valence shell.

 

Example \(\PageIndex{1}\)

Draw an orbital diagram using the shorthand Nobel Gas Configuration and use it to derive the electron configuration of phosphorus, Z = 15. How many valance electrons are there in the ground state electron configuration of a neutral phosphorus atom?

Given: atomic number

Asked for: orbital diagram and valence electron configuration for phosphorus

Strategy:

1. Locate the nearest noble gas preceding phosphorus in the periodic table. Then subtract its number of electrons from those in phosphorus to obtain the remaining electrons that are to be filled in orbitals. 
2. Referring to the periodic table above, draw an orbital diagram to represent those remaining electrons. Following Hund’s rule, place the valence electrons in the available orbitals, beginning with the orbital that is lowest in energy. Write the electron configuration from your orbital diagram.
3. Ignore the inner orbitals (those that correspond to the electron configuration of the nearest noble gas) and write the valence electron configuration for phosphorus.

Solution:

Because phosphorus is in the third row of the periodic table, we know that it has a [Ne] closed shell with 10 electrons. We begin by subtracting 10 electrons from the 15 in phosphorus. The additional five electrons are placed in the next available orbitals, which Figure 6.29 tells us are the 3s and 3p orbitals:

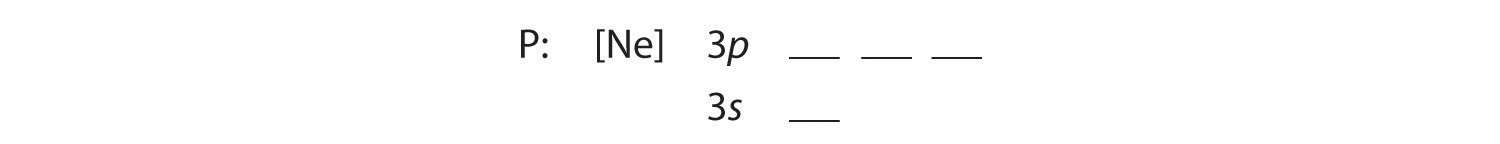
Because the 3s orbital is lower in energy than the 3p orbitals, we fill it first:

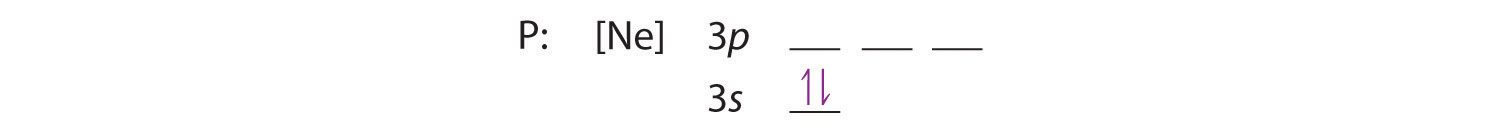
Hund’s rule tells us that the remaining three electrons will occupy the degenerate 3p orbitals separately but with their spins aligned:

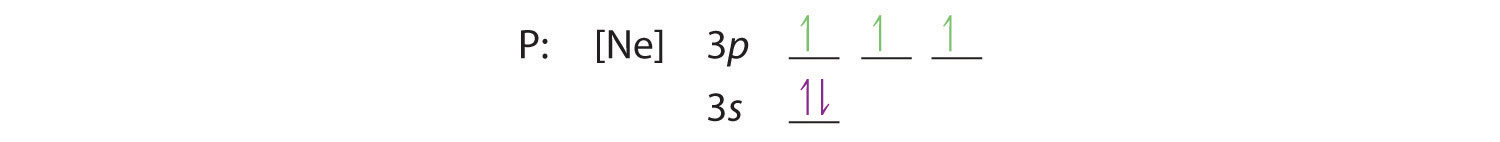
The electron configuration is [Ne]3s²3p³. 

There are 5 valence electrons from the highest shell (n=3) [Ne]3s²3p³ 

 

Exercise \(\PageIndex{1}\) 

Draw an orbital diagram and use it to derive the Nobel Gas electron configuration of chlorine, Z = 17. How many valence electrons are found in a neutral ground state chlorine atom?

Answer: [Ne]3s²3p⁵; 7 

 

Note: Brining It Full Circle 

In chapter 2, we discussed numbering the main group elements using "A" convention. So, phosphorus is in group 5A and chlorine is in group 7A. Now that we have learned to determine electron configuration, we realize that phosphorus has 5 valence electrons and chlorine has 7 valance electrons. The group number ((using the "A" convention) for main group elements  reveals the number of valence electrons in an atom! 

 

 

Electron Configuration of Transition Metals and Inner Transition Metals 

 

So far, we have studied the electron configuration for elements in periods 1-3 on the periodic table in which we filled s and p orbitals. When we get to period 4-7 on the periodic table, we will require the use of the d and f orbitals for transition metals and inner transition metals. Let's take a look at a few examples on how to write the electron configuration for such elements. 

 

Example \(\PageIndex{2}\)

Write the complete ground state (spdf) electron configuration of yttrium? What is the Nobel Gas Configuration? How many valence electrons are found in the ground state electron configuration for yttrium? 

SOLUTION

Start with the straightforward problem of finding the electron configuration of the element yttrium. As always, refer to the periodic table. The element yttrium (symbolized Y) is a transition metal, found in the fifth period and in Group 3. In total it has thirty-nine electrons. Starting from period 1 on th periodic table

 

1s^2	row 1	2 electrons
2s^22p^6	row 2	8 electrons
3s^23p^6	row 3	8 electrons
4s^23d^104p^6 although the "d" block begins in period 4 on the periodic table, it should actually be shifted up one period since at n=3, there are s, p , and d orbitals.  Therefore, the d orbitals will always  be one principle quantum number (n) behind the s and p orbitals.	row 4	18 electrons

5s^24d^1	row 5	3 electrons
	Total	39 electrons

 

Solution : 

Electron Configuration: 1s² 2s² 2p⁶ 3s² 3p⁶ 4s² 3d¹⁰ 4p⁶ 5s² 4d¹

Noble Gas Configuration: 1s² 2s² 2p⁶ 3s² 3p⁶ 4s² 3d¹⁰ 4p⁶ 5s² 4d¹ : [Kr] 5s² 4d¹ 

Number of valence electrons: 2 valence electrons that come from the highest shell (n=5).  [Kr] 5s² 4d¹ 

 

 

Example \(\PageIndex{3}\)

Write the electron configuration of mercury (Z = 80), showing all the inner orbitals. What is the nobel gas configuration? How many valence electrons are in the ground state electron configuration of mercury? 

Given: atomic number

Asked for: complete electron configuration

Strategy:

Using the orbital diagram in Figure 6.8.1 and the periodic table as a guide, fill the orbitals until all 80 electrons have been placed.

Solution:

By placing the electrons in orbitals following the order shown in Figure 6.8.1 and using the periodic table as a guide, we obtain

1s^2	row 1	2 electrons
2s^22p^6	row 2	8 electrons
3s^23p^6	row 3	8 electrons
4s^23d^104p^6	row 4	18 electrons
5s^24d^105p^6	row 5	18 electrons
6s^24f^145d^10 After the 6s orbital is filled, 4f fills next (can hold 14 electrons) because it lower in energy than 5d.  Then, the 10 remaining electrons will go in the 5d orbital. The f orbitals will always be one principle quantum number(n) behind the d orbitals.	row 6	26 electrons
	Total	80 electrons

 

Solution: 

Electron Configuration: 1s²2s²2p⁶3s²3p⁶4s²3d¹⁰4p⁶5s²4d¹⁰5p⁶6s²4f¹⁴5d¹⁰ 

Nobel Gas Configuration: 1s²2s²2p⁶3s²3p⁶4s²3d¹⁰4p⁶5s²4d¹⁰5p⁶6s²4f¹⁴5d¹⁰ : [Xe]6s²4f¹⁴5d¹⁰

Number of valence electrons: two valance shells coming from highest shell number (n=6): [Xe]6s²4f¹⁴5d¹⁰

 

 

Exercise \(\PageIndex{2}\)

Although element 114 is not stable enough to occur in nature, two isotopes of element 114 were created for the first time in a nuclear reactor in 1999 by a team of Russian and American scientists. Write the complete electron configuration for element 114. How many valence electrons are found in the ground state electron configuration for Element 114?

Answer: 1s²2s²2p⁶3s²3p⁶4s²3d¹⁰4p⁶5s²4d¹⁰5p⁶6s²4f¹⁴5d¹⁰6p⁶7s²5f¹⁴6d¹⁰7p² ; 4 valence electrons (from 7s and 7p orbitals. Also, elemenet 114 is in Group 4A, so it will have the same number of valence electrons as carbon and other group 4A elements)

 

Exercise \(\PageIndex{3}\)

After completing the electron configuration for elements in  all rows of the periodic table, what can be concluded about where the valence electrons come from? That is, what subshell(s) do valence electrons typically reside in? 

Answer

s and p orbitals. Since d orbitals are always one shell behind s and p orbitals, and f orbitals are always two shells behind s and p, then it can be concluded that the highest shell number will always be for s and p orbitals, where the valence electrons reside. 

 

 

Exceptions

 

In several cases, the ground state electron configurations are different from those predicted using th periodic table and the Aufbau Principle.  Some of these anomalies occur as the 3d orbitals are filled. For example, the observed ground state electron configuration of chromium is [Ar]4s¹3d⁵ rather than the predicted [Ar]4s²3d⁴. Similarly, the observed electron configuration of copper is [Ar]4s¹3d ¹⁰ instead of [Ar]s²3d ⁹. The actual electron configuration may be rationalized in terms of an added stability associated with a half-filled (ns¹, np³, nd⁵, nf ⁷) or filled (ns², np⁶, nd¹⁰, nf ¹⁴) subshell. Given the small differences between higher energy levels, this added stability is enough to shift an electron from one orbital to another. In heavier elements, other more complex effects can also be important, leading to some of the additional anomalies. For example, cerium has an electron configuration of [Xe]6s²4f¹5d¹, which is impossible to rationalize in simple terms. In most cases, however, these apparent anomalies do not have important chemical consequences. Table 1 summarizes some of those exceptions: 

Table 1: Exceptions to Electron Configuration Trends

Period 4:	Period 5:
Chromium: Z:24 [Ar] 3d^54s^1	Niobium: Z:41 [Kr] 5s^1 4d^4
Copper: Z:29 [Ar] 3d^104s^1	Molybdenum: Z:42 [Kr] 5s^1 4d^5
	Ruthenium: Z:44 [Kr] 5s^1 4d^7
	Rhodium: Z:45 [Kr] 5s^1 4d^8
	Palladium: Z:46 [Kr] 4d^10
	Silver: Z:47 [Kr] 5s^1 4d^10
Period 6:	Period 7:
Lanthanum: Z:57 [Xe] 6s^2 5d^1	Actinium: Z:89 [Rn] 7s^2 6d^1
Cerium: Z:58 [Xe] 6s^2 4f^1 5d^1	Thorium: Z:90 [Rn] 7s^2 6d^2
Gadolinium: Z:64 [Xe] 6s^2 4f^7 5d^1	Protactium: Z:91 [Rn] 7s^2 5f^2 6d^1
Platinum: Z:78 [Xe] 6s^1 4f^14 5d^9	Uranium: Z:92 [Rn] 7s^2 5f^3 6d^1
Gold: Z:79 [Xe] 6s^1 4f^14 5d^10	Neptunium: Z:93 [Rn] 7s^2 5f^4 6d^1
	Curium: Z:96 [Rn] 7s^2 5f^7 6d^1
	Lawrencium: Z:103 [Rn] 7s^2 5f^14 7p^1

 

Summary

Based on the Pauli principle and a knowledge of orbital energies obtained using hydrogen-like orbitals, it is possible to construct the periodic table by filling up the available orbitals beginning with the lowest-energy orbitals (the aufbau principle), which gives rise to a particular arrangement of electrons for each element (its electron configuration). Hund’s rule says that the lowest-energy arrangement of electrons is the one that places them in degenerate orbitals with their spins parallel. For chemical purposes, the most important electrons are those in the outermost principal shell, the valence electrons.

 

Problems

Unless specified, use any method to solve the following problems. Answers are given in noble gas notation.

1. Find the electron configurations of the following:

1. silicon
2. tin
3. lead

2. Scenario: You are currently studying the element iodine and wish to use its electron distributions to aid you in your work.

1. Find the electron configuration of iodine
2. How many unpaired electrons does iodine have?

3. Thought Questions:

1. In your own words describe how to write an electron configuration and why it is an important skill in the study of chemistry.
2. Describe the major concepts (Hunds, Pauli...etc.) and explain why each is a key part of the "tool kit" when describing electron configurations
3. Why is it possible to abbreviate electron configurations with a noble gas in the noble gas notation?

4. Identify the following elements:

1. 1s² 2s² 2p⁶ 3s² 3p⁶ 4s² 3d⁶
2. 1s² 2s² 2p⁶ 3s² 3p⁶ 4s² 3d¹⁰ 4p⁶ 5s² 4d⁷
3. 1s² 2s² 2p⁶ 3s² 3p⁴
4. 1s² 2s² 2p⁶ 3s² 3p⁶ 4s² 3d¹⁰ 4p⁶ 5s² 4d¹⁰ 5p⁶ 6s² 4f¹⁴ 5d¹⁰ 6p⁴

5. Without using a periodic table or any other references, fill in the correct box in the periodic table with the letter of each question. (a)The element with electron configuration: 1s² 2s² 2p⁶ 3s² 3p⁵; (b)A noble gases with f electrons; (c) a fifth-period element whose atoms have three unpaired p electrons; (d) First rowtransition metals having one 4s electron.

Answers

1. Find the electron configuration of the following:

a) silicon: [Ne] 3s² 3p²

b) tin: [Kr] 5s² 4d¹⁰ 5p²

c) lead: [Xe] 6s² 4f¹⁴ 5d¹⁰ 6p²

2. Scenario: You are currently studying the element iodine and wish to use its electron distributions to aid you in your work.

a) Find the electron configuration of iodine

[Kr] 5s² 4d¹⁰ 5p⁵

b) How many unpaired electrons does iodine have?

To find the answer we refer to part a) and look at the valence electrons. We see that iodine has 5 electrons in the p orbitals. We know that the full p orbitals will add up to 6. Using the Hund's rule and Pauli exclusion principals we can make a diagram like the following:

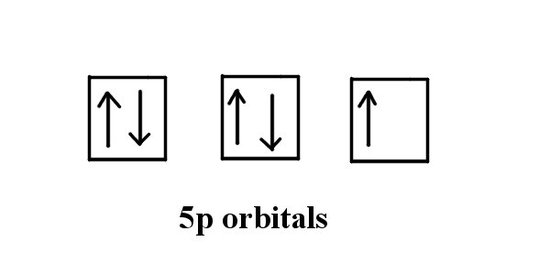
The answer is one.

3. Thought Questions:

a) In your own words describe how to write an electron configuration and why it is an important skill in the study of chemistry.

The first part of this question is straightforward. The second part is slightly more complicated. Because each individual's knowledge of chemistry differs, there are many answers to this question. The important aspect is that we realize that knowing electron configurations helps us determine the valence electrons on an atom. This is important because valence electrons contribute to the unique chemistry of each atom.

b) Describe the major concepts (Hunds, Pauli...etc.) and explain why each is a key part of the "tool kit" when describing electron configurations

This should also be a straightforward question, and if it seems a little difficult refer to the body of this text about these rules and how they relate to creating an electron configuration. Remember to make logical connections! We know that the main "tools" we have in writing electron configurations are orbital occupation, the Pauli exclusion principle, Hund's rule, and the Aufbau process. Orbitals are occupied in a specific order, thus we have to follow this order when assigning electrons. The Pauli exclusion principle states that no two electrons can have the same four quantum numbers . The fourth quantum number, which refers to spin, denotes one of two spin directions. This means that in one orbital there can only be two electrons and they mus have opposite spins. This is important when describing an electron configuration in terms of the orbital diagrams. Hund's rule states that electrons first occupy the similar energy orbitals that are empty before occupying those that are half full. This is especially helpful when determining unpaired electrons. The Aufbau process denotes the method of "building up" each subshell before moving on to the next; we first fill the 2s orbitals before moving to the 2p orbitals.

c) Why is it possible to abbreviate electron configurations with a noble gas in the noble gas notation?

We know that the noble gas has all of its orbitals filled; thus it can be used as a "shorthand" or abbreviated method for writing all of the electron configurations after 1s.

4. Identify the following elements:

a) 1s² 2s² 2p⁶ 3s² 3p⁶ 4s² 3d⁶

The element is iron, Fe

b) 1s² 2s² 2p⁶ 3s² 3p⁶ 4s² 3d¹⁰ 4p⁶ 5s² 4d⁷

The element is Rhodium, Rh

c) 1s² 2s² 2p⁶ 3s² 3p⁴

The element is Sulfur, S

d) 1s² 2s² 2p⁶ 3s² 3p⁶ 4s² 3d¹⁰ 4p⁶ 5s² 4d¹⁰ 5p⁶ 6s² 4f¹⁴ 5d¹⁰ 6p⁴

The element is Polonium, Po

5. Without using a periodic table or any other references, fill in the correct box in the periodic table with the letter of each question. (a) The element with electron configuration: 1s² 2s² 2p⁶ 3s² 3p⁵; (b)A noble gases with f electrons; (c) a fifth-period element whose atoms have three unpaired p electrons; (d) First row transition metals having one 4s electron.

 

 

Contributors 

• Original Source 

• Modified by Ronia Kattoum (UA of Little Rock)