7.2: Atomic Subshell Energies and Electron Assignments

Learning Objectives 

• Rank the energy levels of subshells based on the Aufbau Principle for filling electrons in orbitals 
• Explain the ranking order of subshells using effective nuclear charge 

Now you can determine the electronic structure of every element in the Periodic Table. The process of describing each atom’s electronic structure consists, essentially, of beginning with hydrogen and adding one proton and one electron at a time to create the next heavier element in the table.All stable nuclei other than hydrogen also contain one or more neutrons. Because neutrons have no electrical charge, however, they can be ignored in the following discussion. Before demonstrating how to do this, however, we must introduce the concept of electron spin and the Pauli principle.

 

Order of Filling Orbitals

Occupation of Orbitals

Electrons fill orbitals in a way to minimize the energy of the atom. Therefore, the electrons in an atom fill the principal energy levels in order of increasing energy (the electrons are getting farther from the nucleus). This is known as the Aufbau principle, coming from the German word "Aufbau" meaning "builidng up". The order of levels filled looks like this:

1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, and 7p

 

You may have wondered why, for example, does the 4s orbital fill before the 3d orbital. One would think that the the thirds shell (n=3) would be completely full before we go on to the fourth shell (n=4). However, within a given principal shell (n) of a multielectron atom, the orbital energies increase with increasing l. An ns orbital always lies below the corresponding np orbital, which in turn lies below the nd orbital. In essence, you can think of electrons filling in "n+l " order. If you have an equal "n + l"  value for two orbitals, then electrons will occupy the orbital with the lower "n" value. The following figure illustrates the energy orbitals for each subshell and their filling order according to the aufbau principle. 

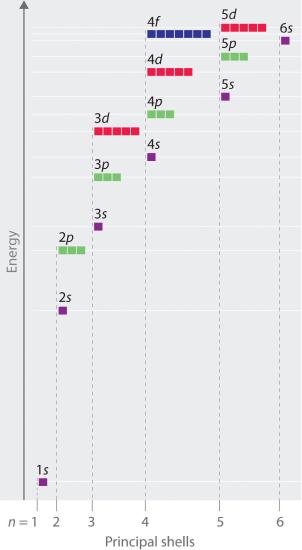
Figure 6.7.16.7.1: Orbital Energy Level Diagram for a Typical Multielectron Atom: notice how the orbitals are assigned in order of increasing "n + l" value. 

 

Example \(\PageIndex{1}\)

Rank the following subshells in order of increasing energy. 

4s, 4d, 4f, 5p 

Solution: 

Strategy: Determine the "n + l " number for each energy level 

4s = (4+0) = 4

4d= (4+2) = 6 

4f= (4+3)= 7

5p= (5+1) = 6 

 

Solution: 4s<4d<5p<4f 

Even though 4d and 5p have the same "n + l " value, the subshell with the lowest "n" value will have the lower energy level. Notice that even though the 5p subshell has an n=5 value, it has a lower energy level than 4f because overall "n + l "  is lower for 5p than for 4f. 

  

 

It may same like a time consuming task to determine the order of electron filling for each subshell. One way to remember this pattern for filling order is to make a table like the one below and use vertical lines to determine which subshells correspond with each other.

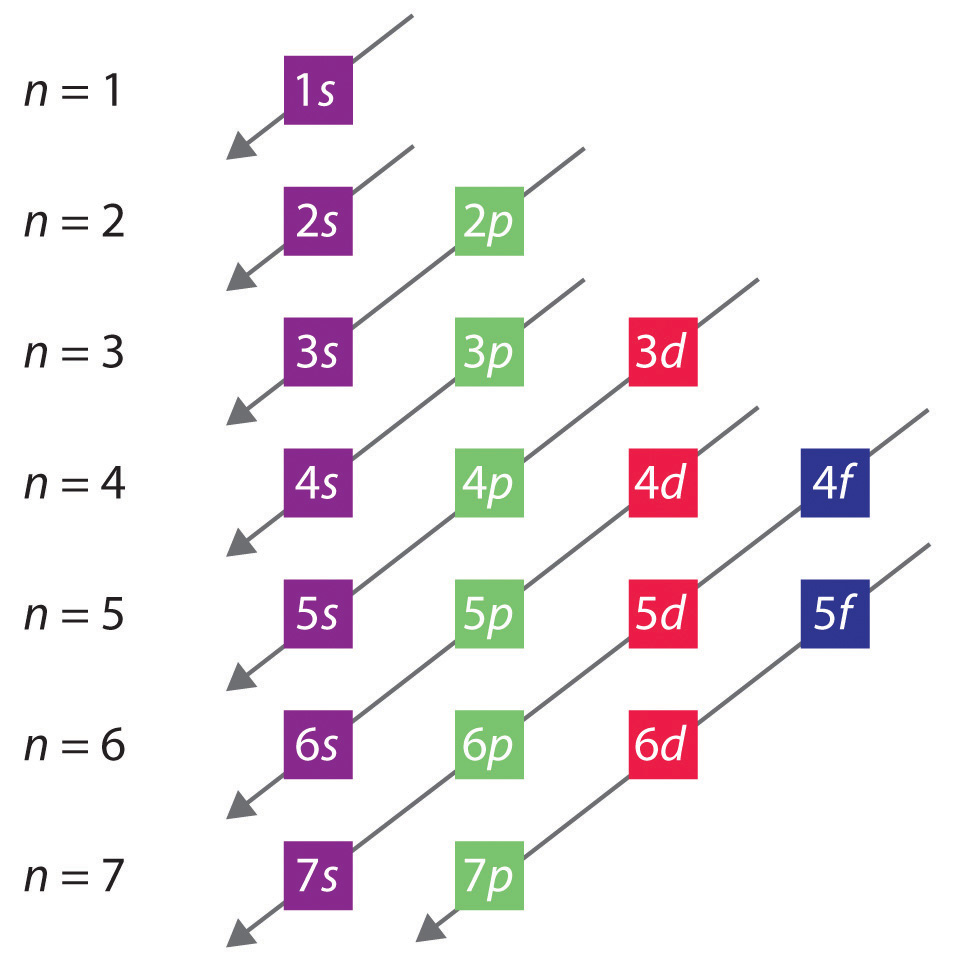
Yet another strategy, perhaps the most useful to chemists, is to use the periodic table to determine the energy levels of orbitals in subshells:

 

Each orbital can be represented by specific blocks on the periodic table. The s-block is the region of the alkali metals including helium (Groups 1 & 2), the d-block are the transition metals (Groups 3 to 12), the p-block are the main group elements from Groups 13 to 18, and the f-block are the lanthanides and actinides series.  

Effective Nuclear Charge 

 

We have discussed how to determine the order for filling electrons in the orbitals of their respective subshell based on increasing energy, but we have not discussed why this is the case. These energy differences are caused by the effects of shielding and penetration, the extent to which a given orbital lies inside other filled orbitals. For an atom or an ion with only a single electron, we can calculate the potential energy by considering only the electrostatic attraction between the positively charged nucleus and the negatively charged electron. When more than one electron is present, however, the total energy of the atom or the ion depends not only on attractive electron-nucleus interactions but also on repulsive electron-electron interactions. When there are two electrons, the repulsive interactions depend on the positions of both electrons at a given instant, but because we cannot specify the exact positions of the electrons, it is impossible to exactly calculate the repulsive interactions. Consequently, we must use approximate methods to deal with the effect of electron-electron repulsions on orbital energies.

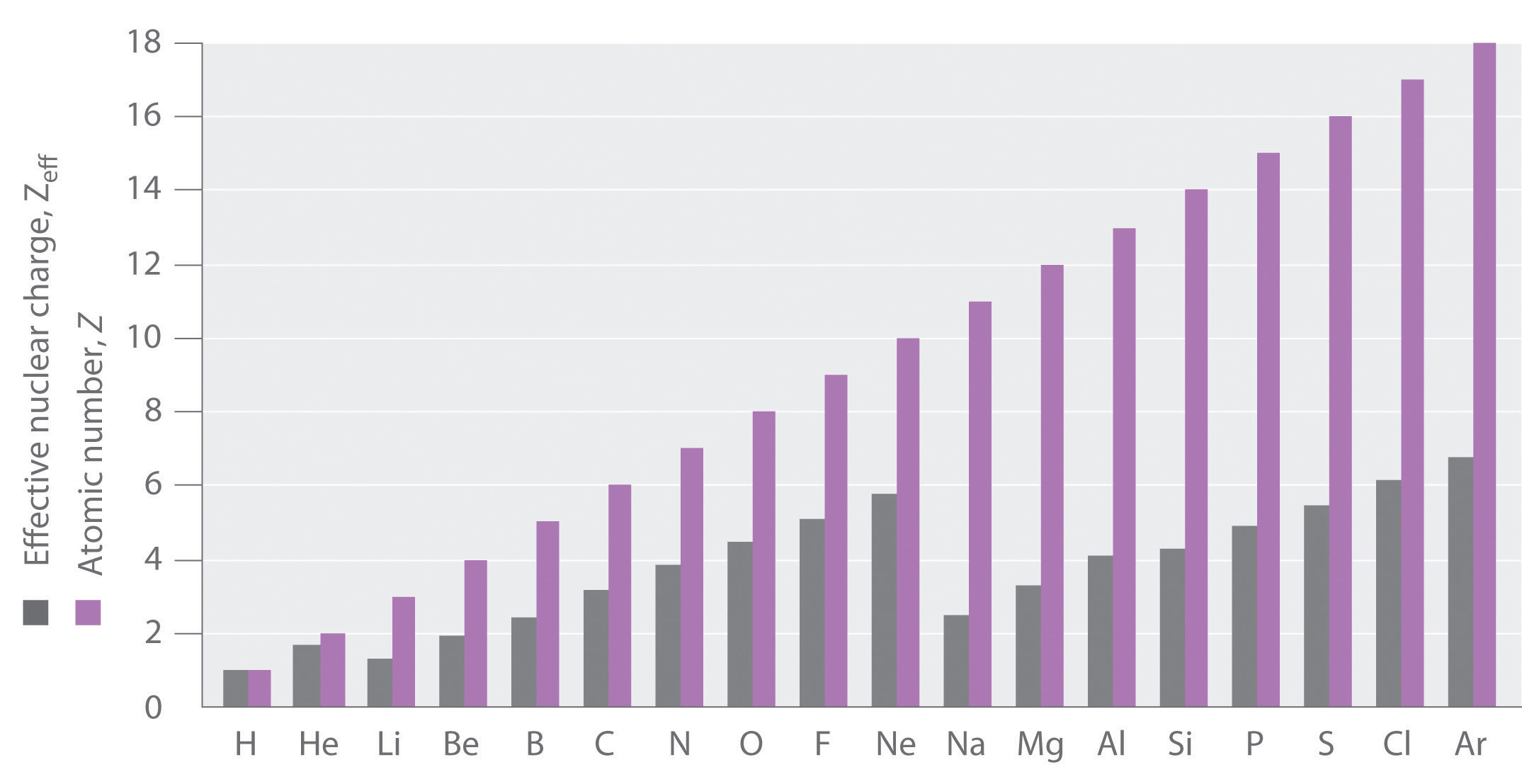
Figure \(\PageIndex{1}\): Relationship between the Effective Nuclear Charge Z_eff and the Atomic Number Z for the Outer Electrons of the Elements of the First Three Rows of the Periodic Table. Except for hydrogen, Z_eff is always less than Z, and Z_eff increases from left to right as you go across a row.

If an electron is far from the nucleus (i.e., if the distance r between the nucleus and the electron is large), then at any given moment, most of the other electrons will be between that electron and the nucleus. Hence the electrons will cancel a portion of the positive charge of the nucleus and thereby decrease the attractive interaction between it and the electron farther away. As a result, the electron farther away experiences an effective nuclear charge (Z_eff) that is less than the actual nuclear charge Z. This effect is called electron shielding. As the distance between an electron and the nucleus approaches infinity, Z_eff approaches a value of 1 because all the other (Z − 1) electrons in the neutral atom are, on the average, between it and the nucleus. If, on the other hand, an electron is very close to the nucleus, then at any given moment most of the other electrons are farther from the nucleus and do not shield the nuclear charge. At r ≈ 0, the positive charge experienced by an electron is approximately the full nuclear charge, or Z_eff ≈ Z. At intermediate values of r, the effective nuclear charge is somewhere between 1 and Z: 1 ≤ Z_eff ≤ Z. Thus the actual Z_eff experienced by an electron in a given orbital depends not only on the spatial distribution of the electron in that orbital but also on the distribution of all the other electrons present. This leads to large differences in Z_eff for different elements, as shown in Figure \(\PageIndex{2}\) for the elements of the first three rows of the periodic table. Notice that only for hydrogen does Z_eff = Z, and only for helium are Z_eff and Z comparable in magnitude.

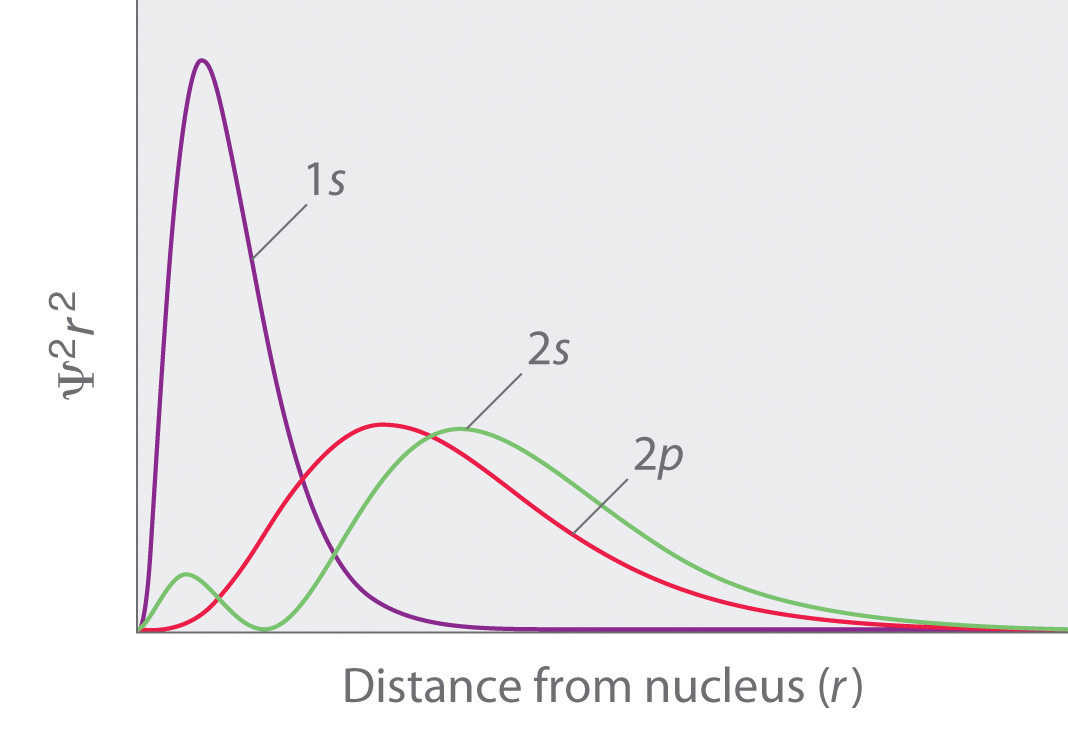
Figure \(\PageIndex{2}\): Orbital Penetration. A comparison of the radial probability distribution of the 2s and 2p orbitals for various states of the hydrogen atom shows that the 2s orbital penetrates inside the 1s orbital more than the 2p orbital does. Consequently, when an electron is in the small inner lobe of the 2s orbital, it experiences a relatively large value of Z_eff, which causes the energy of the 2s orbital to be lower than the energy of the 2p orbital.

Because of the effects of shielding and the different radial distributions of orbitals with the same value of n but different values of l, the different subshells are not degenerate in a multielectron atom. For a given value of n, the ns orbital is always lower in energy than the np orbitals, which are lower in energy than the nd orbitals, and so forth. As a result, some subshells with higher principal quantum numbers are actually lower in energy than subshells with a lower value of n; for example, the 4s orbital is lower in energy than the 3d orbitals for most atoms.

Except for the single electron containing hydrogen atom, in every other element \(Z_{eff}\) is always less than \(Z\).

Summary

The calculation of orbital energies in atoms or ions with more than one electron (multielectron atoms or ions) is complicated by repulsive interactions between the electrons. The concept of electron shielding, in which intervening electrons act to reduce the positive nuclear charge experienced by an electron, allows the use of hydrogen-like orbitals and an effective nuclear charge (Z_eff) to describe electron distributions in more complex atoms or ions. The degree to which orbitals with different values of l and the same value of n overlap or penetrate filled inner shells results in slightly different energies for different subshells in the same principal shell in most atoms.

 

Contributors

• Modified by Ronia Kattoum 
• Original Source