5.2 Specific Heat Capacity
- Page ID
- 158433
Learning Objectives
- Define heat capacity and specific heat capacity and differentiate between the two terms
- Deduce which substance will have greatest temperature changed based on specific heat capacities
- Calculate unknown variables based on known variables using the specific heat equation
Heat Capacity
The heat capacity of a substance is defined as the amount of heat it takes to raise the temperature of a substance by 1°C. In equation form, this can be represented as the following:
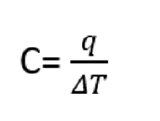 or
or 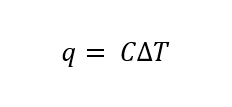
Note: You can determine the above equation from the units of Capacity (energy/temperature). That is if a constant has units, the variables must fit together in an equation that results in the same units. So C equals something with energy in the numerator and temperature in the denominator. Now, you need to use some common sense here, as we are adding heat, not work, and adding heat changes the temperature, it does not make the temperature. So the right side is a ΔT, and not a T.
In words, heat capacity is the substance's ability to resist change in temperature upon exposure to a heat source.A substance with a small heat capacity cannot hold a lot of heat energy and so warms up quickly. On the other hand, a substance with a high heat capacity can absorb much more heat without its temperature drastically increasing. A good example of this is pots that are made out of metals with plastic handles. The metal has a low heat capacity and the plastic handles have a high heat capacity. So, upon exposure to the same amount of heat, the pot gets much hotter, but the handles still remain at a temperature that you can tolerate when you grab onto them.
So, the heat capacity depends on the identity of the material and the quantity of material. For example, even if a cup of water and a gallon of water have the same temperature, the gallon of water holds more heat because it has a greater mass than the cup of water. That is why splattering boiling water on your arm does not do as much damage to the skin as, say, spilling a pot of water on your arm. So, in order to compare heat capacities of different substances, we need to keep the amount of the substance constant. Let's take a look how we can do that.
Specific Heat Capacity
The specific heat capacity is the amount of heat it takes to change the temperature of one gram of substance by 1°C. So, we can now compare the specific heat capacity of a substance on a per gram bases. This value also depends on the nature of the chemical bonds in the substance, and its phase.
q = mc\(\Delta T,\: \: \: c=\frac{q(J)}{m(g)\Delta T(K)}\)
Note: Capital "C" is the Heat Capacity of an object, lower case "c" is the specific heat capacity of a substance. The heat capacity of an object made of a pure substance is, C=mc. If the material an object is made of is uniform in composition, than you can calculate the specific heat capacity for that object, and use it to predict the heat capacity of another object of the same material but different mass. So doubling the mass of an object doubles its heat capacity. Also, some texts use the symbol "s" for specific heat capacity.
It should be noted that just as for heat capacity, the units of specific heat capacity must align with the units of the equation, and so you can calculate the equation from the units, as long as you realize J is a unit of energy, and we are talking heat, not work, g is a unit of mass, and °C is a unit of temperature, although here, it stand for temperature change (ΔT).
Video 5.2.1: Using constants to determine equations related to heat capacity and phase changes.
Is specific heat capacitance an extensive or intensive property?
The specific heat capacity is intensive, and does not depend on the quantity, but the heat capacity is extensive, so two grams of liquid water have twice the heat capacitance of 1 gram, but the specific heat capacity, the heat capacity per gram, is the same, 4.184 (J/g.K).
| Substance | Symbol (state) | Specific Heat (J/g °C) |
|---|---|---|
| helium | He(g) | 5.193 |
| water | H2O(l) | 4.184 |
| ethanol | C2H6O(l) | 2.376 |
| ice | H2O(s) | 2.093 (at −10 °C) |
| water vapor | H2O(g) | 1.864 |
| nitrogen | N2(g) | 1.040 |
| air | mixture | 1.007 |
| oxygen | O2(g) | 0.918 |
| aluminum | Al(s) | 0.897 |
| carbon dioxide | CO2(g) | 0.853 |
| argon | Ar(g) | 0.522 |
| iron | Fe(s) | 0.449 |
| copper | Cu(s) | 0.385 |
| lead | Pb(s) | 0.130 |
| gold | Au(s) | 0.129 |
| silicon | Si(s) | 0.712 |
Table 5.2.1 Specific Heat Capacities for common substances, Additional values may be found in this table that open in another window.
Note: The specific heat capacity depends on the phase (look at ice liquid water and water vapor)
Exercise \(\PageIndex{1}\)
If you add the same amount of heat to an equal mass of liquid water, solid gold, and solid iron, which would end up having the highest temperature?
- Answer
-
Solid Gold. They all have the same mass and are exposed to the same amount of heat. So, the one with the lowest specific heat would have the highest temperature. It has the lowest resistance to temperature change when exposed to heat. If you ever reached into an oven to grab your food with a gold bracelet on, you may have experience the low specific heat capacity of gold. Metals have low heat capacities and thus undergo rapid temperature rises when heat is applied.
Not can we only estimate which substance will have the highest temperature upon heat exposure, we can calculate the final temperature. Let's take a look at how we can use the specific heat equation to calculate the final temperature:
Example \(\PageIndex{2}\)
What is the final temperature if 100.0 J is added to 10.0 g of Aluminum at 25oC? CAl = 0.902J/(g.Co)
Solution
Video Tutor:
We can also use the specific heat equation to determine the identity of the unknown substance by calculating its specific heat capacity.
Example \(\PageIndex{1}\)
Identify an unknown metal using the table of specific heat capacities if its temperature is raised 22.0oC when 51.26J is added to 10.0g of the metal.
Solution
Video Tutor:
Contributors:
- Robert Belford (UA of Little Rock)
- Ronia Kattoum (UA of Little Rock)

