7.3: Atomic Properties and Periodic Trends
- Page ID
- 52827
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
Now that we have an understanding of the electron configurations of the periodic table we are ready to tackle periodic trends in atomic properties. This is a very important section as it will allow us to predict behavior of atoms of the various elements. For example, if two ions have the same charge, the smaller ion forms a stronger bond because it can get closer to the counter ion. So knowing the radius of ions can help us predict ionic bond strengths.
Atomic Radius
The atomic radius is generally stated as being the total distance from an atom’s nucleus to the outermost orbital of its electrons. In simpler terms, it can be defined as something similar to the radius of a circle, where the center of the circle is the nucleus and the outer edge of the circle is the outermost orbital of electron. As you begin to move across or down the periodic table, trends emerge that help explain how atomic radii change. With the exception of the 1s orbitals the nuclear charge the valence shell electrons feel is not the full nuclear charge (Z), but a reduced charge due to shielding caused by the negative charge of the inner shell (core) electrons. We call this the effective nuclear charge, (\(Z_{eff}\)).
\[Z_{eff} < Z_{real}\]
We shall see that this effective nuclear charge influences the size of an atom or ion.
Now determining the size of an atom is actually impossible because according to the Heisenberg Uncertainty Principle we never really know where an electron is, and is going at the same time. But if we look at two bonded atoms we can approximate the size by looking at the distances between the atoms, that is, by looking at bond lengths we can get an approximation of the size of the atoms. We will take two approaches based on the type of bond.
Covalent Radius
When a covalent bond is present between two identical atoms, the covalent radius can be determined. When two atoms of the same element are covalently bonded, the radius of each atom will be half the distance between the two nuclei because they equally attract the electrons. The distance between two nuclei will give the diameter of an atom, and the covalent radius is half this diameter.
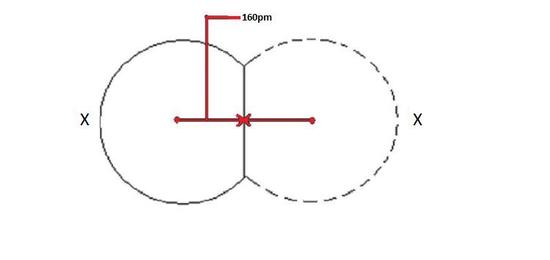
Figure \(\PageIndex{1}\): Covalent radii is one half the distance between two nuclei for a homonuclear bond.
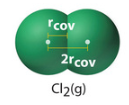
Some compounds like the noble gasses do not form bonds and you can cool them down until they form a solid, and measure the difference between them, which is know as the Van der Waals atomic radius
 |
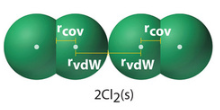 |
Figure \(\PageIndex{2}\): On left is the covalent atomic radius of chlorine, on the right is the van der Waals atomic radi which comes from solid chlorine. These are not necessarily equal
Ionic Radius
Ionic radius are more complicated because the anion and cation are often of vastly different sizes. Now as we shall see, anions are larger than neutral molecules because they gain electrons, and metals are smaller than neutral atoms because they lose electrons. So it is very common for the anion to be larger than the cation. As we shall see in Chapter 12 (section 12.2) of the second semester we can determine the size of ionic ions by looking at the structure of their crystal lattice. What is important to note here is that you can not use the internuclear distance as you can with covalent bonds, because the ion sizes are not equal.
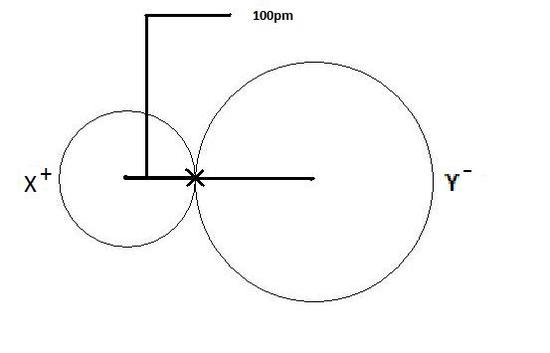 Figure \(\PageIndex{3}\): Ionic radii of cation and anion are not necessarily equal
Figure \(\PageIndex{3}\): Ionic radii of cation and anion are not necessarily equal
Metallic Radius
At first glance you would think you could predict metallic radii the same way you do for covalent, that it would be one half the distance between two metal atoms. As we will learn in Chapter 12 (section 12.1) metals form a variety of different crystal lattice structures and in section 12.1.2 we will learn how to calculate the atomic radii of a metal atom for three different crystal structures. If the metals touch edge to edge along an axis then the atomic radius is one half the distance between the nuclei (as in Figure \(\PageIndex{1}\)).
Periodic Trends in Atomic Radius
There are two general periodic trends in atomic radii. The radii increase as you go down a group, and decrease as you go across a period. These trends are shown in Figures \(\PageIndex{4}\) and \(\PageIndex{5}\)
 |
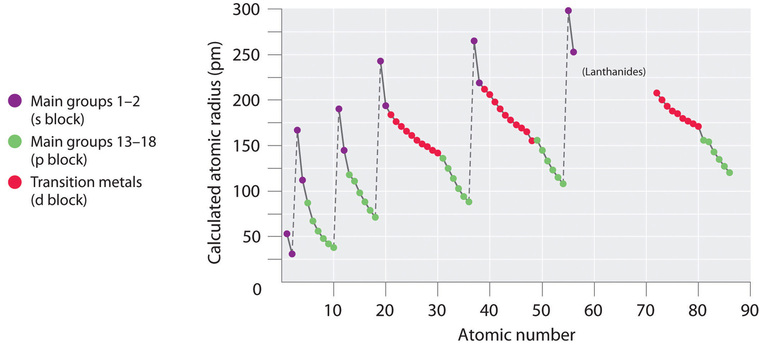 |
Figure \(\PageIndex{4}\): On left is the general periodic trend for atomic radius and on the right are group trends.
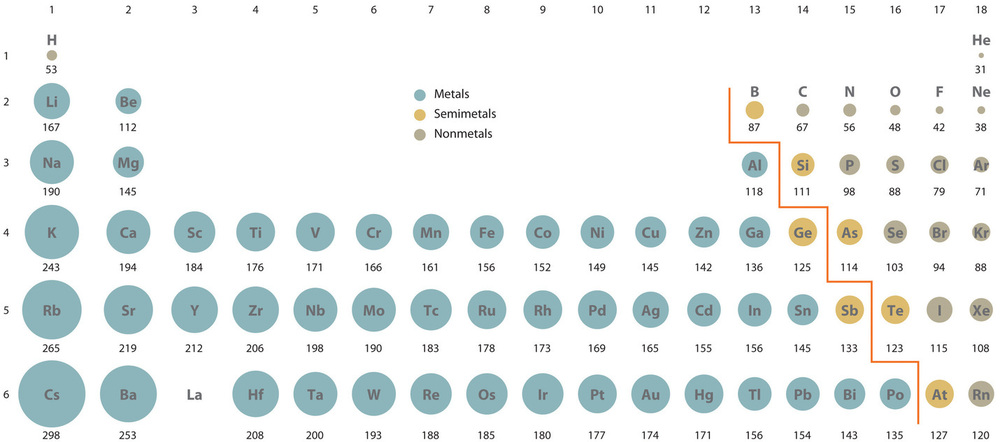
Trend 1: Increased radii going down a group. This one is easy to see, as in going down a group the principle quantum number goes up and you are effectively adding a new shell. It should be noted that valence shells have isoelectronic electron configurations (bottom row of table 7.2.1.) and you are increasing the number of filled core shells. This increase in the number of core electrons results in a larger radii for the valence electrons.
Trend 2: Decreased radii going across a period. This trend takes a bit more thought, but you are changing the valence shell electron configuration while maintaining the same core electron configuration. Core electrons spend more time between valence electrons and the nucleus and so are better at shielding. That is, when a core electron is between a valence electron and the nucleus the valence electron the magnitude of the positive charge the valence electron feels is diminished, and so the effective nuclear charge is decreased. Electrons in the same "shell" repel each other and so fill it in a manner where they are as far apart as possible, and so are not as effective at shielding each other as core electrons. So as you go across a period you increase both the number protons and electrons, but the electrons within a shell are dispersed in a manner that they do not shield each other effectively, and so the effective nuclear charge goes up.
\[\underbrace{Z_{Eff}}_{Effective \\ Nuclear \\ Charge} = \underbrace{Z_{Real}}_{Actual \\ Nuclear \\ Charge}-\underbrace{S}_{Shielding \\ by \; core \\ electrons*}\]
*NOTE: This is not saying that valence shell electrons do not shield each other, you need to look at the shape of the wave function and you can see that valence electrons actually do penetrate core orbitals (Figure \(\PageIndex{6}\), but that core electrons are much better at shielding valence electrons, and so as you go across a periodic table the electrons feel a greater effective nuclear charge, which pulls them in tighter and decreases the radius.
Exercise \(\PageIndex{1}\)
Arrange these atoms in order of decreasing radii and explain why; Si, Cl, Mg, F, Ca
- Answer
-
Answer: Ca > Mg > Si> Cl>F.
Explanation:
- Ca > Mg because it has a higher principle quantum number (higher shell is further from nucleus)
- Mg > Si because Si has has greater ZEff and is thus smaller
- Si > Cl because Cl has greater ZEff and is thus smaller
- Cl > F because it has a higher principle quantum number (higher shell is further from nucleus)
When you change periods (add both a proton and an electron to a Nobel gas) you form an alkali metal and there is a huge increase in atomic size because now you have completely filled a shell). That is for example, The six 3p orbitals of argon do not effectively shield each other because they are in the valence shell, but they very effectively shield the 4s orbital of potassium, and so there is a huge increase in the radii as you move from argon to potassium.
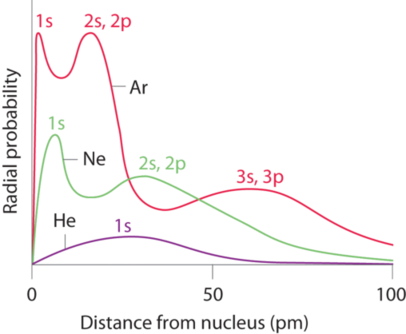
It should also be noted that as you increase the number of protons core shells are pulled in closer to the nucleus. This is shown in Figure \(\PageIndex{6}\) where the 1s orbital in Argon feels the nuclear charge of 18 protons and so is pulled in tighter than the 1s of Neon (10 protons), which in turn is much tighter than the 1s of helium. But only for helium is the 1s the valence electron.
\[1s_{He} > 1s_{Ne}>1s_{Ar} \\but \\ 1s_{He} < 2s_{Ne}<3s_{Ar} \\ and \; so \\r_{Ar}>r_{Ne} >r_{He}\]
So you have to be careful when reading questions.
Exercise \(\PageIndex{2}\)
Indicate if the following are true, and if not, explain why
- radius of K > radius Na because the 1s orbital of K is greater than the 1s orbital of Na.
- radius of K > radius Na because the 1s orbital of K is greater than the 3s orbital of Na
- Answer a
-
FALSE, the 1s orbital of K < the 1s orbital of Na because there is a larger nuclear charge.
- Answer b
-
FALSE, the 1s orbital of K < the 3s orbital of Na, but the 4s orbital of K > than the 3s orbital of Na, and it is the valence shell that determines the "size" of the atom.
Atomic Radii of Monatomic Cations and Anions
Here you are changing the number of electrons of the parent atom without changing the number of protons, and the trend is simple. If you add electrons and form an anion, it is bigger because there are more electrons. If you remove electrons and make a cation it is smaller, because there are fewer electrons. This trend is observed in Figure \(\PageIndex{7}\).
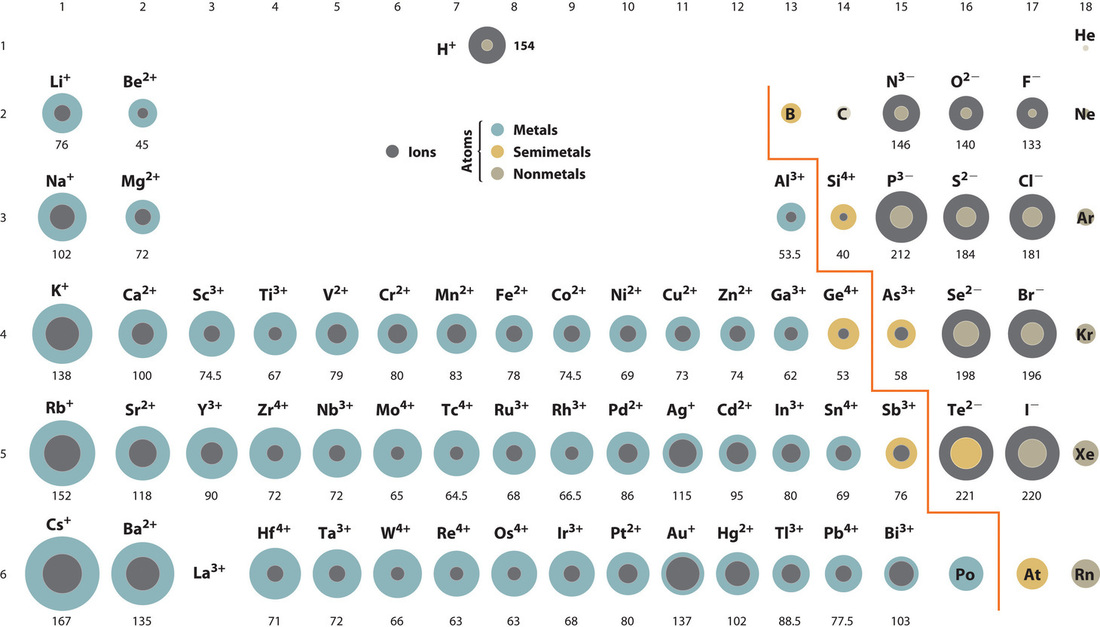
Figure \(\PageIndex{7}\): Ionic Radii (in Picometers) of the Most Common Ionic States of the s-, p-, and d-Block Elements.Gray circles indicate the sizes of the ions shown; colored circles indicate the sizes of the neutral atoms. Source: Ionic radius data from R. D. Shannon, “Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides,” Acta Crystallographica 32, no. 5 (1976): 751–767.
Isoelectronic Series
You note that many cations and anions are isoelectronic to a noble gas, with the nonmetal gaining electrons and the metal losing electrons until the have the same number as a nobel gas (they are isoelectronic to the nobel gas). This results in an isoelectronic series where the number of electrons is constant but the number of protons changes. So the more protons hold the electrons in tightest
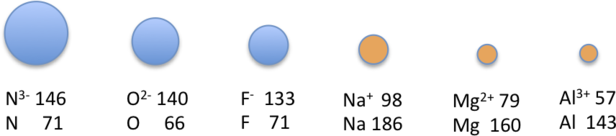
Figure \(\PageIndex{8}\): Anions and cations that are isoelectronic to the nobel gas Neon (the all have a [He]2s22p6 electron configuration).
Ionization Energy (I)
The ionization energy is the minimum energy required to remove an electron from an isolated gas phase chemical species in its ground (lowest energy) state. This is always an endothermic process. The removal of an electron from a neutral atom is its first ionization state, as indicated by the following equation:
\[X_{(g)} + Energy \rightarrow X^+_{(g)}+ e^-_{(g)}\]
First Ionization Energy of Sodium (I1) :
\[Na_{(g)} \rightarrow Na^+_{(g)}+ e^-_{(g)} \; \; I_1=496kJ/mol \]
Any atom other than hydrogen can have successive ionization energies as you take off successively more electrons
Second Ionization Energy of Sodium
\[Na^+_{(g)} \rightarrow Na^{2+}_{(g)} + e^- \; \; I_2=4,562 kJ/mol\]
Atoms that have low ionization energies are easy to ionize and so tend to form cations. It must be emphasized that these are for gas phase atoms where each atom is an isolated unit. Note, ionization energy has units of kJ/mol. In physics this is often treated as the ionization potential and expressed in units of electron volts.
\[1\; eV/atom = 96.49\; kJ/mol\]
Factors that Influence Ionization Energy
- Effective Nuclear Charge: The greater the nuclear charge the greater the Coulombic attraction and the higher the ionization energy. Note, the effective nuclear charge is the true nuclear charge minus any shielding effects of core electrons (ZEff = Z-S)
- Number of "Shells": The greater the number of shells the further the valence electron is from the nuclueus and the easier it is to remove, lowering the ionization energy.
- Orbital Occupancy: Electron configurations can influence ionization energies, for example, filled s orbitals can have a shielding effect on p orbitals of the same period, and electron spin pairing energies can influence ionization energies. That is, if you have two electrons in the same orbital the electron-electron repulsion between them can reduce the ionization energy.
The Noble gasses have the highest ionization energies because they have filled outer shells and thus exeperience very high effective nuclear charges. Helium has the highest because it is the smallest and has no core electrons to shield its valence electrons. Elements in the lower left of the periodic table (Cesium and Francium) have the lowest ionization energies, and are the easiest to ionize.
There are two types of periodic trends we need to understand. Those of the first ionization energy, and those of higher order ionization energies.
Exercise \(\PageIndex{3}\)
True/False and justify your answer: Elements with high ionization energies easily lose electrons and form cations
- Answer
-
False, elements with low ionization energies are easy to ionize because it does not take much energy. Elements with high ionization energies, like the noble gasses take a lot of energy to ionize.
First Ionization Energy Trends
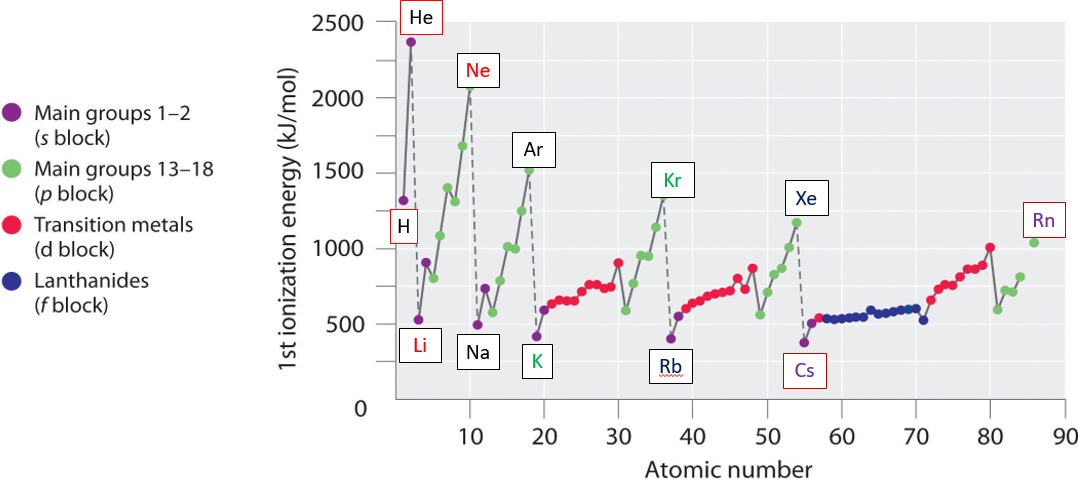
Going down a group is easy, there is an isoelectronic valence shell configuration and the ionization energy decreases because the electrons of each successive "shell" are further from the nucleus, and thus easier to remove. Going across a period requires looking at the electron configurations of each shell and taking into account electron-electron interactions. The general trend is increasing ionization energy because of increasing effective nuclear charge, but there are significant deviations from this that must be taken into account. Figure \(\PageIndex{9}\) shows the periodic trends in first ionization energies. The peaks are the noble gasses, which have the highest ionization potential
 |
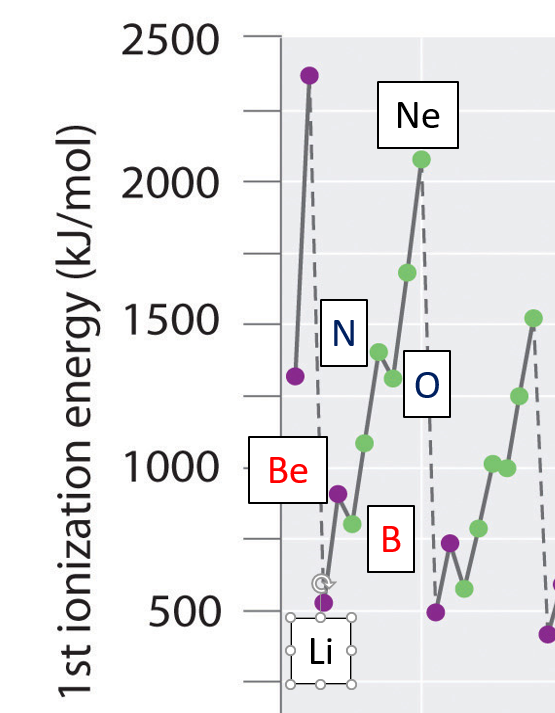 |
\(\PageIndex{9}\): Periodic trends in first ionization energy (left) with focus on second and third period (right)
What is clear from Figure \(\PageIndex{9}\) is that there is not a linear increase in ionization ionization energy across each period, but some clear deviations. For the representative elements (s and p blocks) of the second and third period there is sort of a lightning bolt shape, and it is instructive to examine these in more detail.
Groups 2 and 3 (Be-B and Mg-Al) Exceptions
The explanation lies with the structures of boron and aluminum. The outer electron is removed more easily from these atoms than the general trend in their period would suggest.
| Be | 1s22s2 | 1st I.E. = 900 kJ mol-1 | ||
| B | 1s22s22px1 | 1st I.E. = 799 kJ mol-1 |
You might expect the boron value to be more than the beryllium value because of the extra proton. Offsetting that is the fact that boron's outer electron is in a 2p orbital rather than a 2s. 2p orbitals have a slightly higher energy than the 2s orbital, and the electron is, on average, to be found further from the nucleus. This has two effects.
- The increased distance results in a reduced attraction to the nucleus and so a reduced ionization energy.
- The 2p orbital is screened not only by the 1s2 electrons but, to some extent, by the 2s2 electrons as well (remember, s orbitals penetrate and have inner lobes). That also reduces the pull from the nucleus and so lowers the ionization energy.
The explanation for the drop between magnesium and aluminum is the same, except that everything is happening at the 3-level rather than the 2-level.
| Mg | 1s22s22p63s2 | 1st I.E. = 736 kJ mol-1 | ||
| Al | 1s22s22p63s23px1 | 1st I.E. = 577 kJ mol-1 |
The 3p electron in aluminum is slightly more distant from the nucleus than the 3s, and partially screened by the 3s2 electrons as well as the inner electrons. Both of these factors offset the effect of the extra proton.
Groups 5 and 6 (N-O and P-S) Exceptions
Once again, you might expect the ionization energy of the group 6 element to be higher than that of group 5 because of the extra proton. What is offsetting it this time?
| N | 1s22s22px12py12pz1 | 1st I.E. = 1400 kJ mol-1 | ||
| O | 1s22s22px22py12pz1 | 1st I.E. = 1310 kJ mol-1 |
The screening is identical (from the 1s2 and, to some extent, from the 2s2 electrons), and the electron is being removed from an identical orbital. The difference is that in the oxygen case the electron being removed is one of the 2px2 pair. The repulsion between the two electrons in the same orbital means that the electron is easier to remove than it would otherwise be. The drop in ionization energy at sulfur is accounted for in the same way.
Exercise \(\PageIndex{4}\)
Rank the elements of the second period of the periodic table in order of increasing ionization energy
- Answer
-
Li<B<Be<C<O<N<F<Ne
Higher Order Ionization Energies
If an atom possesses more than one electron, the amount of energy needed to remove successive electrons increases steadily. We can define a first ionization energy (I1), a second ionization energy (I2), and in general an nth ionization energy (In) according to the following reactions:
\[ E_{(g)} \rightarrow E^+_{(g)} +e^- \;\;\ I_1=\text{1st ionization energy} \]
\[ E^+_{(g)} \rightarrow E^{2+}_{(g)} +e^- \;\;\ I_2=\text{2nd ionization energy} \]
\[ E^{2+}_{(g)} \rightarrow E^{3+}_{(g)} +e^- \;\;\ I_3=\text{3rd ionization energy}\]
Values for the ionization energies of \(Li\) and \(Be\) listed in Table \(\PageIndex{1}\) show that successive ionization energies for an element increase steadily; that is, it takes more energy to remove the second electron from an atom than the first, and so forth. There are two reasons for this trend. First, the second electron is being removed from a positively charged species rather than a neutral one, so in accordance with Coulomb’s law, more energy is required. Second, removing the first electron reduces the repulsive forces among the remaining electrons, so the attraction of the remaining electrons to the nucleus is stronger.
| Reaction | Electronic Transition | \(I\) | Reaction | Electronic Transition | \(I\) |
|---|---|---|---|---|---|
| \(Li_{(g)}\rightarrow Li^+_{(g)} + e^-\) | \(1s^22s^1 \rightarrow 1s^2 \;+ \; e^- \) | I1 = 520.2 | \(Be_{(g)} \rightarrow Be^+_{(g)}+e^-\) | \(1s^22s^2 \rightarrow 1s^22s^1 \;+ \; e^- \) | I1 = 899.5 |
| \(Li^+_{(g)} \rightarrow Li^{2+}_{(g)} +e^-\) | \(1s^2 \rightarrow 1s^1 \;+ \; e^- \) | I2 = 7298.2 | \(Be^+_{(g)} \rightarrow Be^{2+}_{(g)} +e^-\) | \(1s^22s^1 \rightarrow 1s^2 \;+ \; e^- \) | I2 = 1757.1 |
| \(Li^{2+}_{(g)} \rightarrow Li^{3+}_{(g)} + e^-\) | \(1s^1 \rightarrow 1s^0 \;+ \; e^- \) | I3 = 11,815.0 | \(Be^{2+}_{(g)} \rightarrow Be^{3+}_{(g)}+e^-\) | \(1s^2 \rightarrow 1s^1 \;+ \; e^- \) | I3 = 14,848.8 |
| \(Be^{3+}_{(g)} \rightarrow Be^{4+}_{(g)}+e^-\) | \(1s^1 \rightarrow 1s^0 \;+ \; e^- \) | I4 = 21,006.6 |
The most important consequence of the values listed in Table \(\PageIndex{1}\) is that the chemistry of \(Li\) is dominated by the \(Li^+\) ion, while the chemistry of \(Be\) is dominated by the +2 oxidation state. The energy required to remove the second electron from \(Li\)
\[Li^+_{(g)} \rightarrow Li^{2+}_{(g)} + e^− \label{7.4.5}\]
is more than 10 times greater than the energy needed to remove the first electron. Similarly, the energy required to remove the third electron from \(Be\)
\[Be^{2+}_{(g)} \rightarrow Be^{3+}_{(g)} + e^− \label{7.4.6}\]
is about 15 times greater than the energy needed to remove the first electron and around 8 times greater than the energy required to remove the second electron. Both \(Li^+\) and \(Be^{2+}\) have 1s2 closed-shell configurations, and much more energy is required to remove an electron from the 1s2 core than from the 2s valence orbital of the same element. The chemical consequences are enormous: lithium (and all the alkali metals) forms compounds with the 1+ ion but not the 2+ or 3+ ions. Similarly, beryllium (and all the alkaline earth metals) forms compounds with the 2+ ion but not the 3+ or 4+ ions. The energy required to remove electrons from a filled core is prohibitively large and simply cannot be achieved in normal chemical reactions.
| Element | 1st | 2rd | 3th | 4th | 5th | 6th | 7th |
|---|---|---|---|---|---|---|---|
| Na | 496 | 4562 | |||||
| Mg | 738 | 1451 | 7733 | ||||
| Al | 577 | 1817 | 2745 | 11580 | |||
| Si | 786 | 1577 | 3232 | 4356 | 16090 | ||
| P | 1060 | 1903 | 2912 | 4957 | 6274 | 21270 | |
| S | 999.6 | 2251 | 3361 | 4564 | 7013 | 8496 | 27110 |
| Cl | 1256 | 2297 | 3822 | 5158 | 6542 | 9362 | 11020 |
| Ar | 1520 | 2666 | 3931 | 5771 | 7238 | 8781 | 12000 |
These are the ionization energies for the period three elements. Notice how Na after in the second I.E, Mg in the third I.E., Al in the fourth I.E., and so on, all have a huge increase in energy compared to the proceeding one. This occurs because the proceeding configuration was in a stable octet formation; therefore it requires a much larger amount of energy to ionize.
Exercise \(\PageIndex{5}\)
An element in the second row of the periodic table shows the following trend in ionization energies
| 1st(kJ/mol) | 2nd(kJ/mol) | 3rf(kJ/mol) | 4th(kJ/mol) | 5th(kJ/mol) | 6th(kJ/mol) |
| 1086.45 | 2352.62 | 4620.47 | 6222.28 | 37831.0 | 47277.1 |
What is the identity of the element?
- Answer
-
Carbon, because the jump from the 4th to the 5th ionization energy is huge, indicating the 5th electron is a core electron, and so there are 4 valence shell electrons., which would be carbon.
Electron Affinities (EA)
Electron Affinity it typically described as the energy change in units of kJ/mol when an electron is added to a chemical species (atom in this case). A negative EA indicates an exothermic reaction and the product state is lower in energy and thus favored. Most textbooks relate this energy change to the following equation:
\[\underbrace{A(g) +e^- \rightarrow A^-(g)}_{\text{Electron Affinity of A}} \label{13} \]
The IUPAC goldbook definition is actually the "Energy required to detach an electron from the singly charged negative ion" for the process, which is actually the negative of the ionization potential (I) of the anion.
\[\underbrace{A^- (g) \rightarrow A(g) + e^- }_{\text{Ionization Potential of }A^-} \label{14}\]
At first it seems like there are two different definitions but when you think about it, they make sense. If Equation \(\ref{14}\) requires say that 73kJ/mol must be added to remove an electron from hydride (H-), which is the ionization potential of hydride (not hydrogen), then the reverse reaction, the electron affinity of hydrogen \(\ref{14}\) must be a negative 73 kJ/mol.
\[E_A(A) = -I(A^-)\]
If there is an affinity for an electron the reaction is exothermic (EA<0) and this can become a tongue twister. To keep things straight you should always stick to the sign conventions of thermodynamics, realizing that things tend to go towards the lower energy state and so a negative EA implies an affinity for the electron. That is why the Y-scale of Figure \(\PageIndex{10}\) is inverted (as you go up the numbers get more negative) with chlorine having the highest affinity for an electron with EA=-348.6kJ/mol.
a
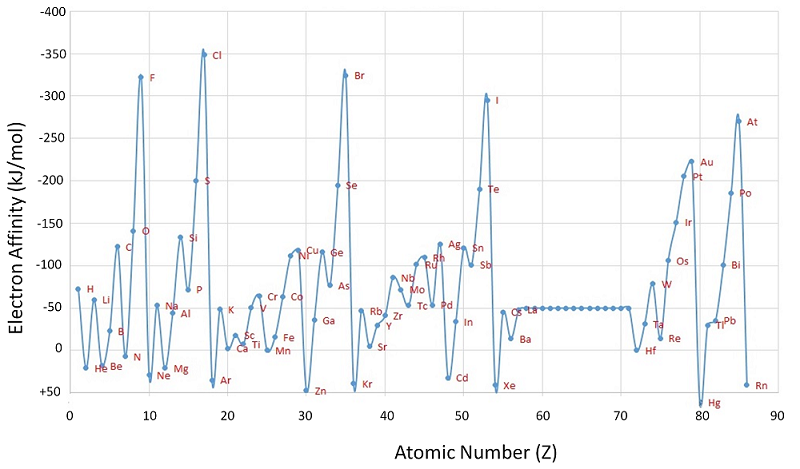
Figure \(\PageIndex{10}\): Chart of periodic trends in Electron Affinity (EA). Note, the values of the Lanthanides are not given in this Figure.
w
A positive (endothermic) electron affinity means you must add energy to form the anion.
a
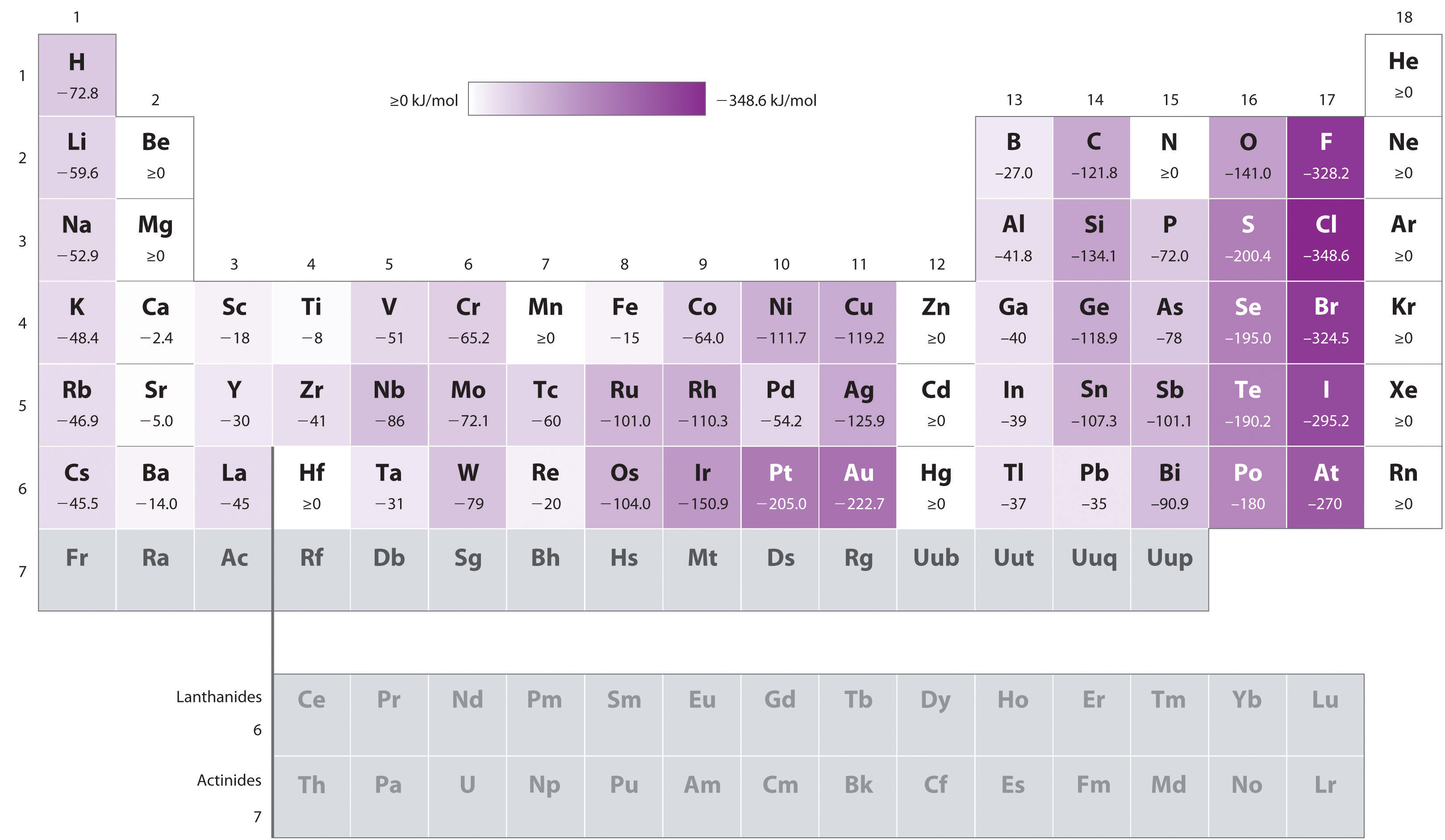
Figure \(\PageIndex{11}\): Values of Electron Affinity (EA) for elements with exothermic values . In looking at Electron Affinities it needs to be understood that these are energy states for an isolated atom or ion where there is no interaction with any other chemical species. Data from Journal of Physical and Chemical Reference Data 28, no. 6 (1999).
Note on Sign convention
The fact that the more exothermic the electron affinity the more an atom has an affinity for an electron has caused some confusion. Here is a table with the signs switched from the ones in Figures \(\PageIndex{10}\) and \(\PageIndex{11}\).
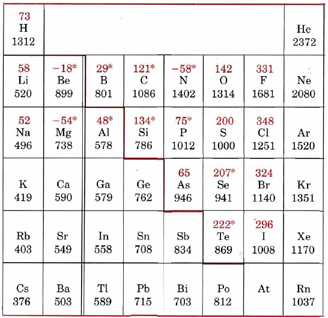
Figure \(\PageIndex{12}\): Table of ionization energies (black) and electron affinities (red). Note how the sign is changed from Figures \(\PageIndex{10}\) and \(\PageIndex{11}\). Values with asterisk (*) are theoretical calculations.
The truth is that there is inconsistent sign convention, and there is justification for both ways. Figure \(\PageIndex{12}\) give fluorine and chlorine positive electron affinities because they tend to grab an electron, and give nitrogen a negative one because it does not. In this class we will stick to the thermodynamic convention that a negative electron affinity means it is exothermic, and thus the affinity is higher. If you look closely at Figure \(\PageIndex{10}\) you will note that chlorine has the most negative value and is the highest on the chart, that means it has the highest electron affinity. So as you read through this, the more negative EA, the greater the electron affinity.
Periodic Trends in EA
Just like Ionization potentials you must look at the electron configurations to understand the periodic trends in EA.
- Nonmetals other than the noble gasses tend to have negative (exothermic) EAs.
- Noble gasses all have endothermic electron affinities because they have a filled valence shell, and so the added electron is going to the next highest shell (principle quantum number), which is very well shielded and so it does not feel a strong Zeff (Effective Nuclear Charge).
- There is a tendency for EA to increase going across a period (become more exothermic - negative) and this is due to increasing Zeff (until you reach the noble gasses).
- Nitrogen has an endothermic EA because of its electron configuration. As shown in Figure \(\PageIndex{12}\), in accordance with Hunds rule, nitrogen has one electron in all three of the p orbitals and their magnetic moments align. When you add the additional electron to make N-, it is not only being added to an orbital that is already occupied, but it magnetic field is against that of the other electrons.
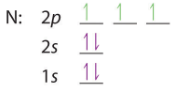 |
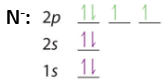 |
| N:[He]2s22p3 | N-: [He]2s22p4 |
- The other group VA elements also show a dip, but are exothermic, and this is for the same reason as Nitrogen.
- Halogens decrease in electron affinity (become less exothermic) going down the group because the valence shell is further away from the nucleus and so the electron being added feels a weaker pull. Fluorine is the exception (it is not higher than chlorine) because it is so small that the electron-electron repulsions interfere with the pull towards the nuclues.
- Alkali metals have negative electron affinities because the s orbital is being filled
Second Electron Affinities
The equations for second and higher electron affinities are analogous to those for second and higher ionization energies:
\[E_{(g)} + e^- \rightarrow E^-_{(g)} \;\;\; \text{energy change=}EA_1 \label{7.5.5}\]
\[E^-_{(g)} + e^- \rightarrow E^{2-}_{(g)} \;\;\; \text{energy change=}EA_2 \label{7.5.6}\]
As we have seen, the first electron affinity can be greater than or equal to zero or negative, depending on the electron configuration of the atom. In contrast, the second electron affinity is always positive because the increased electron–electron repulsions in a dianion are far greater than the attraction of the nucleus for the extra electrons. For example, the first electron affinity of oxygen is −141 kJ/mol, but the second electron affinity is +744 kJ/mol:
\[O_{(g)} + e^- \rightarrow O^-_{(g)} \;\;\; EA_1=-141 \;kJ/mol \label{7.5.7}\]
\[O^-_{(g)} + e^- \rightarrow O^{2-}_{(g)} \;\;\; EA_2=+744 \;kJ/mol \label{7.5.8}\]
Thus the formation of a gaseous oxide (\(O^{2−}\)) ion is energetically quite unfavorable (estimated by adding both steps):
\[O_{(g)} + 2e^- \rightarrow O^{2-}_{(g)} \;\;\; EA=+603 \;kJ/mol \label{7.5.9}\]
Similarly, the formation of all common dianions (such as \(S^{2−}\)) or trianions (such as \(P^{3−}\)) are energetically unfavorable in the gas phase.
Test Yourself
Query \(\PageIndex{1}\)
Contributors and Attributions
Robert E. Belford (University of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert E. Belford, rebelford@ualr.edu. You should contact him if you have any concerns. This material has both original contributions, and content built upon prior contributions of the LibreTexts Community and other resources, including but not limited to:
Some material adopted and/or adapted from
- Jim Clark (Chemguide.co.uk)
- anonymous contributors


