6.4: Wave-Particle Duality
- Page ID
- 52792
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- To understand the wave–particle duality of matter.
- To understand the uncertainty principle
A shortcoming of the Bohr model was that it could only predict the atomic spectra of hydrogen. It in essence treated an electron as a classical object in an orbit around the nucleus, where in reality an electron is a quantum particle that has wave-particle duality. This can be seen with Einstein's photoelectric effect where an electron interacts with a photon, which if it is of sufficient energy, ejects the electron out of an atomic orbital.
The Wave Character of Matter
Einstein initially assumed that photons had zero mass, which made them a peculiar sort of particle indeed. In 1905, however, he published his special theory of relativity, which related energy and mass according to the following equation:
\[ E=mc^{2} \]
And from Planck's equation we know that
\[E= h\nu=h\dfrac{c}{\lambda }\]
equating these gives \[E=h\dfrac{c}{\lambda }=mc^2 \\ \\ or \\ \\ \frac{h}{\lambda} = mc\]
rearranging give
\[\lambda = \frac{h}{mc}\]
In 1922, the American physicist Arthur Compton (1892–1962) reported the results of experiments involving the collision of x-rays and electrons that supported the particle nature of light. At about the same time, a young French physics student, Louis de Broglie (1892–1972), began to wonder whether the converse was true: Could particles exhibit the properties of waves? In his PhD dissertation submitted to the Sorbonne in 1924, de Broglie proposed that a particle such as an electron could be described by a wave whose wavelength is given by
\[\lambda =\dfrac{h}{\text{mv}} \]
where
- h is Planck’s constant,
- m is the mass of the particle, and
- v is the velocity of the particle.
De Broglie extended this concept to all matter. This revolutionary idea was quickly confirmed by American physicists Clinton Davisson (1881–1958) and Lester Germer (1896–1971), who showed that beams of electrons, regarded as particles, were diffracted by a sodium chloride crystal in the same manner as x-rays, which were regarded as waves. It was proven experimentally that electrons do exhibit the properties of waves. For his work, de Broglie received the Nobel Prize in Physics in 1929.
If particles exhibit the properties of waves, why had no one observed them before? The answer lies in the numerator of de Broglie’s equation, which is an extremely small number. As you will calculate in Example 6.4.1, Planck’s constant (6.63 × 10−34 J•s) is so small that the wavelength of a particle with a large mass is too short (less than the diameter of an atomic nucleus) to be noticeable.
Note: in Plancks Equation \(E=h\nu\) that \(\nu\) is the frequency of a wavelengths oscillation while in de Broglie's Equation \(\lambda = \frac{h}{mv} \) v is the velocity, and in fact mv is the momentum (p) and de Broglie's equation is often written as \(\lambda = \frac{h}{p} \), where p is the momentum.
Example 6.4.1
Calculate the wavelength of a baseball, which has a mass of 149 g and a speed of 100 mi/h.
Given: mass and speed of object
Asked for: wavelength
Strategy:
- Convert the speed of the baseball to the appropriate SI units: meters per second.
- Substitute values into Equation 6.4.3 and solve for the wavelength.
Solution:
The wavelength of a particle is given by λ = h/mv. We know that m = 0.149 kg, so all we need to find is the speed of the baseball:
\( v=\left ( \dfrac{100\; \cancel{mi}}{\cancel{h}} \right )\left ( \dfrac{1\; \cancel{h}}{60\; \cancel{min}} \right )\left ( \dfrac{1.609\; \cancel{km}}{\cancel{mi}} \right )\left ( \dfrac{1000\; m}{\cancel{km}} \right ) \frac{min}{60sec}=44.69m/sec\)
B Recall that the joule is a derived unit, whose units are (kg•m2)/s2. Thus the wavelength of the baseball is
\[ \lambda =\dfrac{6.626\times 10^{-34}\; J\cdot s}{\left ( 0.149\; kg \right )\left ( 44.69\; m\cdot s^{-1} \right )}= \dfrac{6.626\times 10^{-34}\; \cancel{kg}\cdot m{^\cancel{2}\cdot \cancel{s}{\cancel{^{-2}}\cdot \cancel{s}}}}{\left ( 0.149\; \cancel{kg} \right )\left ( 44.69\; \cancel{m}\cdot \cancel{s^{-1}} \right )}=9.95\times 10^{-35}\; m \]
(You should verify that the units cancel to give the wavelength in meters.) Given that the diameter of the nucleus of an atom is approximately 10−14 m, the wavelength of the baseball is almost unimaginably small.
Exercise \(\PageIndex{1}\)
Calculate the wavelength of a neutron that is moving at 3.00 × 103 m/s.
- Answer
-
1.32 Å, or 132 pm
Heisenberg Uncertainty Principle
Because a wave is a disturbance that travels in space, it has no fixed position. One might therefore expect that it would also be hard to specify the exact position of a particle that exhibits wavelike behavior. A characteristic of light is that it can be bent or spread out by passing through a narrow slit as shown in the video below. You can literally see this by half closing your eyes and looking through your eye lashes. This reduces the brightness of what you are seeing and somewhat fuzzes out the image, but the light bends around your lashes to provide a complete image rather than a bunch of bars across the image. This is called diffraction.
This behavior of waves is captured in Maxwell's equations (1870 or so) for electromagnetic waves and was and is well understood. Heisenberg's uncertainty principle for light is, if you will, merely a conclusion about the nature of electromagnetic waves and nothing new. DeBroglie's idea of wave particle duality means that particles such as electrons which all exhibit wave like characteristics, will also undergo diffraction from slits whose size is of the order of the electron wavelength.
This situation was described mathematically by the German physicist Werner Heisenberg (1901–1976; Nobel Prize in Physics, 1932), who related the position of a particle to its momentum. Referring to the electron, Heisenberg stated that “at every moment the electron has only an inaccurate position and an inaccurate velocity, and between these two inaccuracies there is this uncertainty relation.” Mathematically, the Heisenberg uncertainty principle is greater than or equal to Planck’s constant h divided by 4π: states that the uncertainty in the position of a particle (Δx) multiplied by the uncertainty in its momentum [Δ(mv)] is greater than or equal to Planck’s constant divided by 4π:
\[ \left ( \Delta x \right )\left ( \Delta \left [ mv \right ] \right )\geqslant \dfrac{h}{4\pi } \]
Because Planck’s constant is a very small number, the Heisenberg uncertainty principle is important only for particles such as electrons that have very low masses. These are the same particles predicted by de Broglie’s equation to have measurable wavelengths.
If the precise position x of a particle is known absolutely (Δx = 0), then the uncertainty in its momentum must be infinite (as dividing by zero equals infinity).
\[ \left ( \Delta \left [ mv \right ] \right )= \dfrac{h}{4\pi \left ( \Delta x \right ) }=\dfrac{h}{4\pi \left ( 0 \right ) }=\infty \]
Because the mass of the electron at rest (m) is both constant and accurately known, the uncertainty in Δ(mv) must be due to the Δv term, which would have to be infinitely large for Δ(mv) to equal infinity. That is, according to Equation 6.4.8, the more accurately we know the exact position of the electron (as Δx → 0), the less accurately we know the speed and the kinetic energy of the electron (1/2 mv2) because Δ(mv) → ∞. Conversely, the more accurately we know the precise momentum (and the energy) of the electron [as Δ(mv) → 0], then Δx → ∞ and we have no idea where the electron is.
Bohr’s model of the hydrogen atom violated the Heisenberg uncertainty principle by trying to specify simultaneously both the position (an orbit of a particular radius) and the energy (a quantity related to the momentum) of the electron. Moreover, given its mass and wavelike nature, the electron in the hydrogen atom could not possibly orbit the nucleus in a well-defined circular path as predicted by Bohr. You will see, however, that the most probable radius of the electron in the hydrogen atom is exactly the one predicted by Bohr’s model.
Example 8.5.2
Calculate the minimum uncertainty in the position of the pitched baseball from Example 8.5.1 that has a mass of exactly 149 g and a speed of 100 ± 1 mi/h.
Given: mass and speed of object
Asked for: minimum uncertainty in its position
Strategy:
- Rearrange the inequality that describes the Heisenberg uncertainty principle (Equation 8.5.7) to solve for the minimum uncertainty in the position of an object (Δx).
- Find Δv by converting the velocity of the baseball to the appropriate SI units: meters per second.
- Substitute the appropriate values into the expression for the inequality and solve for Δx.
Solution:
A The Heisenberg uncertainty principle tells us that (Δx)[Δ(mv)] = h/4π. Rearranging the inequality gives
\( \Delta x \ge \left( {\dfrac{h}{4\pi }} \right)\left( {\dfrac{1}{\Delta (mv)}} \right)\)
B We know that h = 6.626 × 10−34 J•s and m = 0.149 kg. Because there is no uncertainty in the mass of the baseball, Δ(mv) = mΔv and Δv = ±1 mi/h. We have
\( \Delta \nu =\left ( \dfrac{1\; \cancel{mi}}{\cancel{h}} \right )\left ( \dfrac{1\; \cancel{h}}{60\; \cancel{min}} \right )\left ( \dfrac{1\; \cancel{min}}{60\; s} \right )\left ( \dfrac{1.609\; \cancel{km}}{\cancel{mi}} \right )\left ( \dfrac{1000\; m}{\cancel{km}} \right )=0.4469\; m/s \)
C Therefore,
\( \Delta x \geqslant \left ( \dfrac{6.626\times 10^{-34}\; J\cdot s}{4\left ( 3.1416 \right )} \right ) \left ( \dfrac{1}{\left ( 0.149\; kg \right )\left ( 0.4469\; m\cdot s^{-1} \right )} \right ) \)
Inserting the definition of a joule (1 J = 1 kg•m2/s2) gives
\( \Delta x \geqslant \left ( \dfrac{6.626\times 10^{-34}\; \cancel{kg} \cdot m^{\cancel{2}} \cdot s}{4\left ( 3.1416 \right )\left ( \cancel{s^{2}} \right )} \right ) \left ( \dfrac{1\; \cancel{s}}{\left ( 0.149\; \cancel{kg} \right )\left ( 0.4469\; \cancel{m} \right )} \right ) \)
\( \Delta x \geqslant 7.92 \pm \times 10^{-34}\; m \)
This is equal to 3.12 × 10−32 inches. We can safely say that if a batter misjudges the speed of a fastball by 1 mi/h (about 1%), he will not be able to blame Heisenberg’s uncertainty principle for striking out.
Exercise 8.5.2
Calculate the minimum uncertainty in the position of an electron traveling at one-third the speed of light, if the uncertainty in its speed is ±0.1%. Assume its mass to be equal to its mass at rest.
Answer: 6 × 10−10 m, or 0.6 nm (about the diameter of a benzene molecule)
A Bit More on Waves
As de Broglie's equation states that all particles have wave-particle duality, it is prudent to discuss a bit more on the nature of waves.
Wave Interference
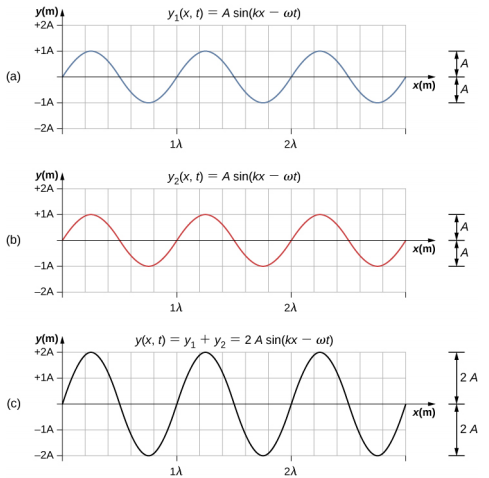
Two waves can interact with each other constructively or destructively.
 |
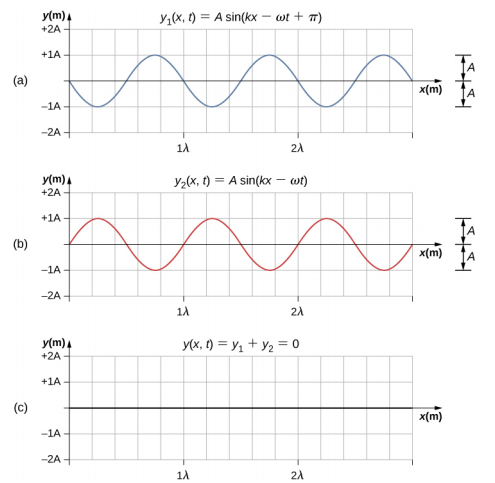 |
Figure \(\PageIndex{1}\): Constructive and destructive interference. Waves (a) and (b) are added together to form wave (c). Both waves are of the same frequency, the ones in the left are in phase and add to each other. The ones on the right are 180o out of phase, and annihilate each other.
A node is where the wave function equals zero and a standing wave has no amplitude.
Standing Waves
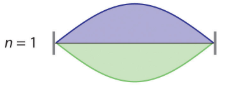
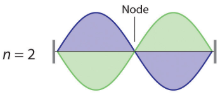
De Broglie also investigated why only certain orbits were allowed in Bohr’s model of the hydrogen atom. He hypothesized that the electron behaves like a standing wave (a wave that does not appear to travel in space). A standing wave is easiest to visualize for a linear wave like the vibration along a string of defined length where the amplitude of motion at the ends of the string is restrained. As the wave front reaches the end of the string a second wave will reflect back towards the first and these two waves will interfere with each other, with all but a few wavelengths annihilating each other through destructive interference. The waves that do not annihilate each other resonate at quantized frequencies and result in standing waves. The first standing wave has a wavelength of twice the length of the string and is called the fundamental (lowest energy standing wave).
\[ L = \dfrac{\lambda }{2} \; \; \therefore \; \; \lambda =2L \]
Higher-energy vibrations are called overtones (the vibration of a standing wave that is higher in energy than the fundamental vibration) and are produced when the string is plucked more strongly; they have wavelengths given by
\[ L = n\dfrac{\lambda }{2} \; \; \therefore \; \; \lambda=\dfrac{2L}{n} \]
where n has any integral value. Thus the resonant vibrational energies of the string are quantized. When plucked, all other frequencies die out immediately. Only the resonant frequencies survive and are heard. Notice in Figure \(\PageIndex{2}\) that all overtones have one or more nodes (the points where the amplitude of a wave is zero), points where the string does not move. The amplitude of the wave at a node is zero.
 |
 |
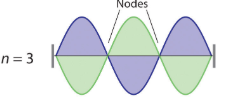 |
Figure \(\PageIndex{2}\): Fundamental and first two overtones for harmonic resonance frequencies along a string of length L Note the number of nodes are quantized as n-1 with n being an integer (the fundamental has no nodes).
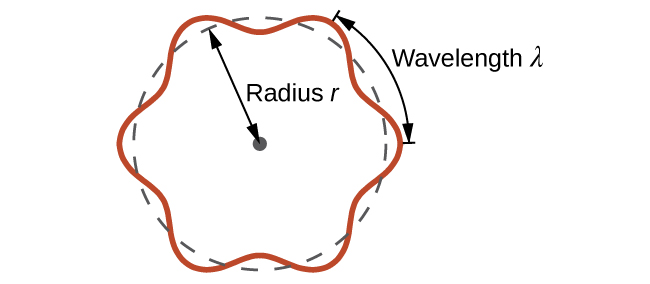
Quantized vibrations and overtones containing nodes are not restricted to one-dimensional systems, such as strings. De Broglie argued that Bohr’s allowed orbits could be understood if the electron behaved like a standing circular wave (Figure \(\PageIndex{3}\)). Here standing wave can only exist if the circumference of the circle is an integral multiple of the wavelength which would result in constructive interference, with all other wavelengths destructively annihilating themselves.
\[2πr = nλ , \; \; n=1,2,3...\]
where r is the radius of the circle.
De Broglie’s idea explained Bohr’s allowed orbits and energy levels nicely: in the lowest energy level, corresponding to n = 1 where one complete wavelength would close the circle. Higher energy levels would have successively higher values of n with a corresponding number of nodes
The following YouTube goes over one, two and three dimensional standing waves and is worth watching.
In reality atoms and their electrons exist in three dimensional space and Erwin Schrödinger extended the concept of standing waves to three dimensions and spherical harmonics, where the standing wave functions could be viewed as the harmonics of a fluid filled surface on a sphere. The Schrödinger wave equation lead to the modern quantum mechanical model of the atom and will introduced in the next section of this Chapter.
Contributors and Attributions
Robert E. Belford (University of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert E. Belford, rebelford@ualr.edu. You should contact him if you have any concerns. This material has both original contributions, and content built upon prior contributions of the LibreTexts Community and other resources, including but not limited to:
Some material adopted and adapted from
- Paul Flowers, et al. Open Stax
- anonymous contributors to LibreText


