2.11: Empirical and Molecular Formulas
- Page ID
- 50439
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)learning objectives
- Distinguish between empirical formula and molecular formula
- Determine empirical formula and molecular formula using percent composition
- Determine empirical formula and molecular formula using mass data
Introduction
Empirical measurements are based on a measurable (empirical) quantity like mass. Knowing the mass of each element in a compound we can determine its formula. There are two types of formulas, empirical and molecular.
Empirical Formula: Lowest whole number ratio of the elements in a compound
Molecular Formula: Actual whole number ratio of the elements in a compound.
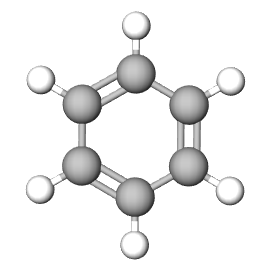
The Empirical formula is the lowest whole number ratio of the elements in a compound. In (section 2.10), we discovered that benzene and acetylene have the same mass percent composition, and thus it is logical that they have the same ratio of elements to each other, that is, they have the same empirical formula.
| Compound | Acetylene | benzene | NaCl |
| Structure | 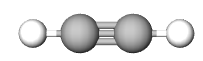 |
 |
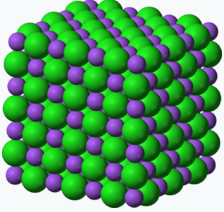 |
| Empirical Formula | CH | CH | NaCl |
| Molecular Formula | C2H2 | C6H6 | not a molecule (use NaCl) |
Figure \(\PageIndex{1}\): Empirical and molecular formulas of several simple compounds.
Empirical Formula
The Empirical formula is the lowest whole number ratio of the elements in a compound. In (section 2.10), we discovered that benzene and acetylene have the same mass percent composition, and thus it is logical that they have the same ratio of elements to each other, that is, they have the same empirical formula.
For salts that do not have homonuclear diatomic ions (like Hg2+2 or O2-2) the empirical formula is the formula we write to describe the salt. Mercury(I)chloride has the empirical formula of HgCl, but the real compound formula is Hg2Cl2 (review table 2.7.3)
Multiple molecules can have the same empirical formula. For example, benzene (C6H6) and acetylene (C2H2) both of the empirical formula of CH (see Figure \(\PageIndex{1}\).
Calculating Empirical Formulas
Steps:
- Obtain Mass of Each Element (in grams)
- if given total mass you need the mass of all but one element (sum of masses equals total mass).
- if given % composition assume 100 g and convert to mass.
- if given % composition you need data for of all but one element (sum of percents equals 100%).
- Calculate # of moles of each element present (from masses and atomic weights).
- You now have a formula representing the mole ratio of the elements in the compound and you need to make these integers.
- Divide # of Moles of each element by the one with the smallest value (forcing it to one and making all other values greater than one).
- Multiply the results of step 3 by the smallest integer which will convert them all to whole numbers.
Note
The trick is to convert decimals to fractions and then multiply by the lowest common denominator (watch video \(\PageIndex{1}\))
| 0.5=\(\frac{1}{2}\) | 0.33=\(\frac{1}{3}\) | 0.67=\(\frac{2}{3}\) | 0.25=\(\frac{1}{4}\) | 0.75=\(\frac{3}{4}\) |
| 0.2=\(\frac{1}{5}\) | 0.4=\(\frac{2}{5}\) | 0.6=\(\frac{3}{5}\) | 0.8=\(\frac{4}{5}\) | 0.167=\(\frac{1}{6}\) |
The following video shows how to calculate the empirical formula for aspiring.
Calculate the empirical formula for aspirin:
Aspirin is made of H, O & C, and was analyzed to contain 60.0% carbon and 35.5% Oxygen.
Video \(\PageIndex{1}\): Empirical formula of aspirin
Example \(\PageIndex{1}\)
A certain compound was found to contain 67.6% C, 22.5% O, and 9.9% H. What is the empirical formula?.
Solution
\[22.5gO\left ( \frac{1molO}{16.00g} \right )= 1.4\Rightarrow \frac{1.4}{1.4}= 1\]
\[67.6gC\left ( \frac{1molC}{12.011g} \right )= 5.63\Rightarrow \frac{5.63}{1.4}= 4\]
\[9.9gH\left ( \frac{1molH}{1.007g} \right )= 9.9\Rightarrow \frac{9.9}{1.4}= 7\]
C4H7O
This Applet comes from the ChemCollective at Carnegie Mellon University. This link will send you to the video and tutorial associated with this applet. Every time you load the page a new problem will load, and there are a series of tiered hints to help you work through the problems.
Exercise \(\PageIndex{1}\): empirical formula
Calculate the Empirical formula for the following
- A 3.3700 g sample of a salt which contains copper, nitrogen and oxygen, was analyzed to contain 1.1418 g of copper and 1.7248 g of oxygen.
- A compound of nitrogen and oxygen that contains 30.43% N by weight.
- A 2.402-g sample of made of C, H, N and O contains 1.121 g of N, 0.161 g H, 0.480 g C, and an unspecified amount of oxygen.
- Answer a
-
CuN2O6
- Answer b
-
NO2
- Answer c
-
N2H4CO
Exercise \(\PageIndex{2}\): empirical formula
Given the empirical formula of the compound in part (a) of the above:
- What could be the formula of the compound.
- What would be the name of the compound, using the formula in the answer from part (a) of this question.
- Answer a
-
Cu(NO3)2
- Answer b
-
Copper(II) nitrate of cupric nitrate
Exercise \(\PageIndex{3}\): empirical formula
In section 2.10.2 we saw that benzene and acetylene both have the same mass percent composition (92.3% C and and 7.7% H), so calculate their empirical formulas
- What is the empirical formula of acetylene (C2H2)?
- What is the empirical formula of benzene (C6H6)? (Knowing (a) the empirical formula of acetylene and (b) that benzene and acetylene have the same mass % composition, cam you answer this without doing any math?)
- Answer a
-
CH
- Answer b
-
CH
Molecular Formula
To calculate the molecular formula we need additional information beyond that of the mass or mass percent composition, we need to know the molar mass of the substance. There are many experimental ways that can be determined, and we will learn some as the semester proceeds. The mass spectrometer that we used to determine the isotopic composition in section 2.3 of this Chapter could be used to determine the molar mass of many unknowns. But there are other techniques, and at this point in the semester, the molar mass will be treated as a given.
The empirical formula represents the lowest whole number ratio of the elements in a molecule while the molecular formula represents the actual formula of the molecule. So the molecular formula must be an integer multiple of the empircal formula, that is it is n times larger where n=1 or 2 or 3 or.... but it is an integer. This gives the following relationship
\[\text{[Molecular Formula = n([Empirical Formula)]}\]
then if we have one mole
\[\text{[Molecular Weight = n([Empirical Weight)]}\]
or
\[n=\frac{\text{[Molecular Weight]}}{\text{[Empirical Weight]}}\]
So you calculate the Empirical formula as above, then determine the weight of one mole, divide that into the molar mass, and that tells you how many times it is bigger, and then multiple the emprical formula by that number.
Let's compare Benzene to acetylene. In video 2.10.2 (section 2.10.2) we saw that benzene and acetylene had the same mass % composition and in exercise 2.11.3 we say they had the same empirical formula
| name: | Benzene | Acetylene |
| Formula Weight | 78.12g/mol | 26.04g/mol |
| Empirical Formula | CH | CH |
| Empirical Formula Weight | 13.017 | 13.017 |
| n=\(\frac{\text{[Molecular Weight]}}{\text{[Empirical Weight]}}\) | \(\frac{78.12}{13.017}=6\) | \(\frac{26.04}{13.017}=2\) |
| Formula = n times empirical formula | 6(CH) = C6H6 | 2(CH) = C2H2 |
Calculating Molecular Formulas
Example \(\PageIndex{2}\)
A certain compound was found to contain 67.6% C, 22.5% O, and 9.9% H. If the molecular weight of the compound was found to be approximately 142 g/mol, what is the correct molecular formula for the compound?
Solution
C4H7O has a empirical weight of
(4)(12.01) + (7)(1.007) + (16.00) = 71.09g/mol
\[\left ( \frac{142g/mol}{71.09g/mol} \right )= 2\]
multiply the coefficients by 2
C8H14O2
Exercise \(\PageIndex{4}\): Molecular formula
Calculate the molecular formula for the following
- A compound has an empirical formula of C2HF has a molar mass of 132.06 g/mol.
- 200.0 g sample of an acid with a molar mass of 616.73g/mol contains 171.36 g of carbon, 18.18g of nitrogen and the rest is hydrogen.
- Strychine has a molar mass of 334 g/mol and percent composition of 75.42%C, 6.63%H and 8.38%N and the rest oxygen.
- Answer a
-
C6H3F3
- Answer b
-
C44N4H32
- Answer c
-
C21N2H22O2
Contributors and Attributions
Robert E. Belford (University of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert E. Belford, rebelford@ualr.edu. You should contact him if you have any concerns. This material has both original contributions, and content built upon prior contributions of the LibreTexts Community and other resources, including but not limited to:
- November Palmer & Emily Choate (UALR)
- Ronia Kattoum (Learning Objectives)


