2.10: Percent Composition
- Page ID
- 50438
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)learning objectives
- Introduce Mass Percent and Mole Fraction
- Calculate Mass Percent from Chemical Formulas
Introduction
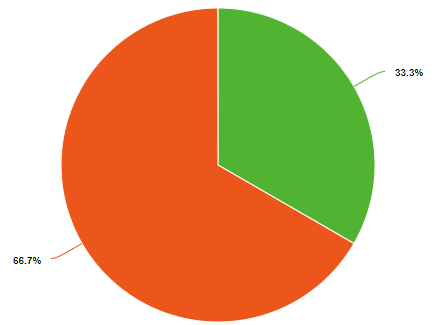
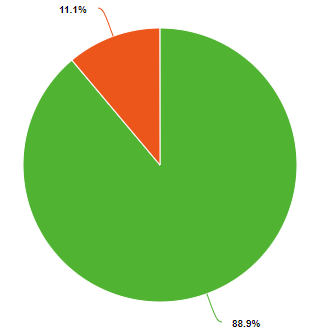
Percent and fraction essentially tell you the same thing, they describe the ratio of a part of the whole. Because a chemical compound has a constant composition, which is defined by is molecular or compound formula, the fraction of each type of element must be constant. For example, water has 3 atoms, one hydrogen and two oxygens. So the fraction of oxygen is 1/3 (33.3%) and the fraction of hydrogen is 2/3rd (66.7%), as exemplified in the left pie chart of Figure \(\PageIndex{1}\). But water weights 16 times as much as hydrogen and so if you could weigh a water molecule, the mass of oxygen would be 16 Daltons, while that of the two hydrogens would be 2 Daltons, so on a mass basis, water if 88.9% oxygen and 11.1% hydrogen. So when we say the fractional or percent composition, we need to identify how we are determining it. Usually, but not always, chemists use percentage for mass and fraction for moles (number of particles).
| Mole Fraction/Percent of Water | Mass Fraction/Percent of Water |
 |
 |
 |
|
Figure \(\PageIndex{1}\): Mole (left) and mass (right) fractions (or percentages) of oxygen and hydrogen in water.
So, is water mostly oxygen or hydrogen? Well, that depends on how you look at it. If you are counting atoms, it is mostly hydrogen. If you are measuring the mass, it is mostly oxygen.
Mass Percent
Mass percent of any element in a compound is 100 time the mass of the element divided by the total mass
\[\mathrm{Mass\: \%\: element=\dfrac{mass\: element}{mass\: compound}\times100\%}\]
One mole of water weights 18 grams, with 2 grams being hydrogen and 16 being oxygen, so the fraction of hydrogen is 2/18 (0.1111) and the fraction oxygen is 16/18 (.8889), and note that the sum of the fractions is 1. The percentage of an element in a compound is 100 times the fraction, so for water the mass percent hydrogen is 11.11% and the mass percent oxygen is 88.89%.
\[\mathrm{Mass\: \%H=\dfrac{mass\: H}{mass\: compound}\times100\%}\]
\[\mathrm{Mass\: \%H=\dfrac{2g}{18g}\times100\%}=11.11%\]
Equations 2.10.4 and 2.10.5 describe the right pie chart in Figure \(\PageIndex{1}\), and note they add to 100%.
Video \(\PageIndex{1}\) shows a technique to calculate the percent composition of a formula that minimizes the amount of work you need to do.
NOTE: Even though mass has units, mass percent is unit-less, and so care needs to be taken to identify what the percent or fraction relates to. Also, because a sample of a pure substance consist of molecules or ionic compounds of the same formula, the percent or fractional value does not depend on the sample size. So one molecule of water has the same percent composition as a gallon of [pure] water.
It should also be noted that as the following two videos show, some formulas have the same percent composition, even though they are different molecules, like acetylene (C2H2) and benzene (C6H6).
Exercise \(\PageIndex{1}\)
What is the mass percent of oxygen in dichlorine heptoxide?
- Answer
-
Mass of Cl in 1 mol Cl2O7 , 2 Cl : 2 x 35.45 g = 70.90 g
Mass of O in 1 mol Cl2O7 , 7 O: 7 x 16.00 g = 112.00 g
Molar mass of Cl2O7 = 182.90 g/mol
\[\% \: \ce{O} = \frac{112.00 \: \text{g} \: \ce{O}}{182.90 \: \text{g}} \times 100\% = 61.24\% \: \ce{O} \nonumber\]
Mole Fraction
The mole fraction of each element in a sample is the number of moles of that in a sample divided by the total number of moles in the sample, and this can be determined by the chemical formula, where it is the number of atoms of that element in the formula divided by the total number of atoms in the formula.
\[\mathrm{mole\: fraction\: of\: an\: element\:=\dfrac{moles\: of\: the\: element}{total\: moles\: in\: compound}}\]
shows the numbers of each type of element and so one mole of water (H2O) has two moles of hydrogen and one mole of water. That is the mole fraction of hydrogen is 2/3 (.6667) and the mole fraction oxygen is 1/3 (.3333), meaning the mole fraction for water is 67% hydrogen and 33% oxygen.
\[\mathrm{mole\: fraction\: H=\dfrac{mole\: H}{total\: mol\: in\: compound}}\]
\[\mathrm{mole\: fraction\: H=\dfrac{2\: mole\: H}{3\: mol}\: =\: 0.667}\]
Equations 2.10.9 and 2.10.10 describe the right pie chart in Figure \(\PageIndex{1}\).
Exercise \(\PageIndex{2}\)
What is the mole fraction of oxygen in dichlorine heptoxide?
- Answer
-
Moles of Cl in 1 mol Cl2O7 = 2 mol Cl
Moles of O in 1 mol Cl2O7 = 7 mol
Total moles in Cl2O7 = 9
\[mole \: fraction \: \ce{O} = \frac{7 \: \text{mol O}}{9 \text{ total moles}} = .778 \nonumber\]
Contributors and Attributions
Robert E. Belford (University of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert E. Belford, rebelford@ualr.edu. You should contact him if you have any concerns. This material has both original contributions, and content built upon prior contributions of the LibreTexts Community and other resources, including but not limited to:
- Ronia Kattoum (Learning Objectives)