2.3: Isotope Abundance and Atomic Weight
- Page ID
- 50428
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)learning objectives
- Define atomic weight
- Calculate atomic weight from percent abundance
- Manipulate the atomic weight equation to calculate various unknown variables
- Distinguish between atomic weight, atomic number, and mass number
Atomic Weight
The atomic weight is the mass of an atom, typically expressed in atomic mass units (amu). For an isotope, it is the mass of the nucleus, that is the mass of the protons and neutrons, as the mass of the electrons are considered negligible. In their natural state only 21 elements exist as single isotopes, that is a sample has nuclei of only one isotope, and these are called the mononuclidic elements. Most elements exist as a mixture of nuclei from multiple isotopes, and these are labeled as the polynuclidic elements. The atomic weight of a monuclidic element is that mass of that nuclide.
For a polynuclidic element the atomic weight is the average weight based on the fractional abundance of each isotope, and this is the value given on the periodic table. Copper has two isotopes, 63Cu (69.15%, mass=62.9300 amu) and 65Cu (30.85%, mass = 64.928 amu), and so the respective mole fractions are 0.6915 and 0.3085, resulting in an average atomic weight of 63.55 amu, even though there is not a single atom that weighs 63.55 amu.
| \[\underbrace{0.6915}_{fraction \; ^{63}Cu}\underbrace{(62.9300\, amu)}_{mass \; ^{63}Cu} + \underbrace{ 0.3085}_{fraction \; ^{65}Cu} \underbrace{(64.928 \,amu)}_{mass \; ^{65}Cu} = \underbrace{63.55\, amu}_{\text{average mass}} \\ note: \; 0.6915 + 0.3085 = 1\] |
Figure \(\PageIndex{1}\): Natural samples of copper contain two isotopes, and its atomic weight is to four significant digits is 63.55 amu, even though there is not a single atom of copper that weights 63.55 amu.
Exercise \(\PageIndex{1}\)
The atomic weight of chorine is ______________and the atomic number of chlorine-35 is________________.
- 35, 17
- 17, 35
- 35.4527; 17
- 35.4527; 35
- Answer
-
C) the atomic weight is the average of mass of all isotopes of chlorine atoms and found below the symbol on the periodic table. The atomic number is the number of protons in all chlorine atoms and is found on the top of the symbol in the periodic table.
Mononuclidic Elements
There are 21 elements with natural occurring samples that have only have one nucleus and are thus classified as mononuclidic. Nineteen of these are stable and two are radioactive (Bi & Th). The term monoisotopic refers to having only 1 stable nucleus, of which there are 26, ninteen of which are mononuclidic, but seven of the monoisotopic elements also have radioactive isotopes and so are not mononuclidic, but polynuclidic.
For a mononuclidic element, the atomic weight is the weight of its isotope. Sodium is a stable mononuclidic element that consists of just one isotope, 23Na.
Figure \(\PageIndex{1}\): Sodium only has one isotope, and note, the uncertainty of this value is expressed by the (2) in 22.989 769 28(2), indicating that the last value has an uncertainty of +/- .000 000 02. Adapted from 2018 IUPAC Technical Report - IPTEI for Education Community, (cc. 4.0), p. 1864.
The following lists the 21 stable mononuclidic elements:
| \(^{27}_{13}Al\) | \(^{75}_{33}As\) | \(^{9}_4Be\) | \(^{209}_{83}Bi^*\) | \(^{133}_{55}Cs\) | \(^{59}_{27}Co\) | \(^{19}_9F\) |
| \(^{197}_{79}Au\) | \(^{165}_{67}Ho\) | \(^{127}_{53}I\) | \(^{55}_{25}Mn\) | \(^{93}_{41}Nb\) | \(^{31}_{15}P\) | \(^{141}_{59}Pr\) |
| \(^{103}_{45}Rh\) | \(^{45}_{21}Sc\) | \(^{23}_{11}Na\) | \(^{159}_{65}Tb\) | \(^{232}_{90}Th^*\) | \(^{169}_{69}Tm\) | \(^{89}_{39}Y\) |
Polynuclidic Elements
The vast majority of elements are polynuclidic, that is, a sample contains a mixture of nuclei from different isotopes. For some samples the fraction of each isotope is constant, while for others itf varies between samples. So there are two types of polynuclidic elements, those with invariant isotopic distributions, and those with variable isotopic distributions.
Constant Isotopic Distributions
For example, copper has two stable isotopes, and is approximately 69% 63Cu and 31% 65Cu by number (not mass). This ratio is constant from sample to sample and so it is invariant. The atomic weight of copper is based on this isotropic distribution and comes out to 63.546 amu, even though there is not a single atom of copper that weighs 63.546 amu (69% of them weigh 63 amu and 31% weigh 65).
Figure \(\PageIndex{3}\): Copper has two stable isotopes as indicated in the pie diagram. Adapted from 2018 IUPAC Technical Report - IPTEI for Education Community, (cc. 4.0), p. 1901.
Lead has 4 stable isotopes as shown in Figure . Lead is a fairly large element and has many radioisotopes, in fact it has 29 isotopes with a half life of less than one hour, seven between an hour and a year, and two with half lives over a year (202Pb = 5.25x104 years & 210Pb = 22.3 years), but these are insignificant to the thousandth position (note the four mole fractions add to one).
Figure \(\PageIndex{4}\): Lead has 4 stable isotopes. Adapted from 2018 IUPAC Technical Report - IPTEI for Education Community, (cc. 4.0), p 2007.
Variable Isotopic Distributions
Until recently, it was thought that the isotopic composition of an element was constant, but now it is realized that these can vary across samples. To date, the following 13 elements have been identified to have a range of isotopic distributions; hydrogen, lithium, boron, carbon, nitrogen, oxygen, magnesium, silicon, sulfur, chlorine, argon, bromine, and thallium. In 2009 the IUPAC Commission on Isotopic Abundances and Atomic Weights introduced an interval notation on atomic weights that expressed the natural occurring variability in the isotopic composition of the elements.
Hydrogen consists of two isotopes, protium (1H, a single proton) and deuterium (2H, a proton and a neutron). The isotopic composition of different samples vary within the defined ranges, so the percent protium ranges from 99.999% to 99.972%. There is a third naturally occurring radioactive isotope of hydrogen, \(^{3}H\) (tritium), which is very rare and has a mole fraction that is so small that it is insignificant compared to protium and deuterium.
Figure \(\PageIndex{5}\): Hydrogen's Isotopic distribution can vary from sample to sample and so IUPAC introduced an interval notation. Adapted from 2018 IUPAC Technical Report - IPTEI for Education Community, (cc. 4.0), p 1839.
These differences can actually show up in the hydrogen atomic weight in river water, where for example, water in the mountains will have a higher proportion of the heavier isotope, and this makes sense, as the heavier isotope would condense into rain easier than the lighter, and water at lower elevations would tend to have more of the lighter isotope. This can be seen in Figure 2.3.6.
Note: The sum of the percent natural abundances of all the isotopes of any given element must total 100%.
Some naturally occurring and artificially produced isotopes are radioactive. All atoms heavier than Bismuth (\(^{209}_{83}Bi\)) are radioactive. However, there are many lighter nuclides that are radioactive. For example, hydrogen has two naturally occurring stable isotopes, \(^{1}H\) and \(^{2}H\) (deuterium), and a third naturally occurring radioactive isotope, \(^{3}H\) (tritium).
Measuring Isotopic Abundances
The Mass Spectrometer is an instrument that allows us to measure the mass of atoms, or more accurately, the mass to charge ratio. In Figure 2.3.8 you can see chlorine gas entering an mass spectrometer. The chlorine has multiple isotopes and is hit with a stream of ionizing electrons which break the bond of Cl2 and strip electrons off the chlorine atoms causing monatomic ions. These are then accelerated down the chamber until they reach a magnetic field that deflects the particles. The angle of deflection depends on both the mass of the particle and the magnetic field strength, with the lighter particles being deflected more for a constant magnetic field strength (the lighter 35Cl+ ions are deflected more than the heavier 37Cl+ ions.) At the end of the chamber is an exit hole with a detector, and as the magnetic field intensity is increased the deflection angle changes, which separates the particles. Note, the mass spectrum in Figure 2.3.8 (b) gives the relative abundance of each isotope, with the peak normalized to the isotope with the highest abundance. So if this ratio was 3:1 that means there are 3 particles of 35Cl for every particle of 37Cl, and the fractional abundance would be 0.75 for 35Cl and 0.25 for 37Cl.
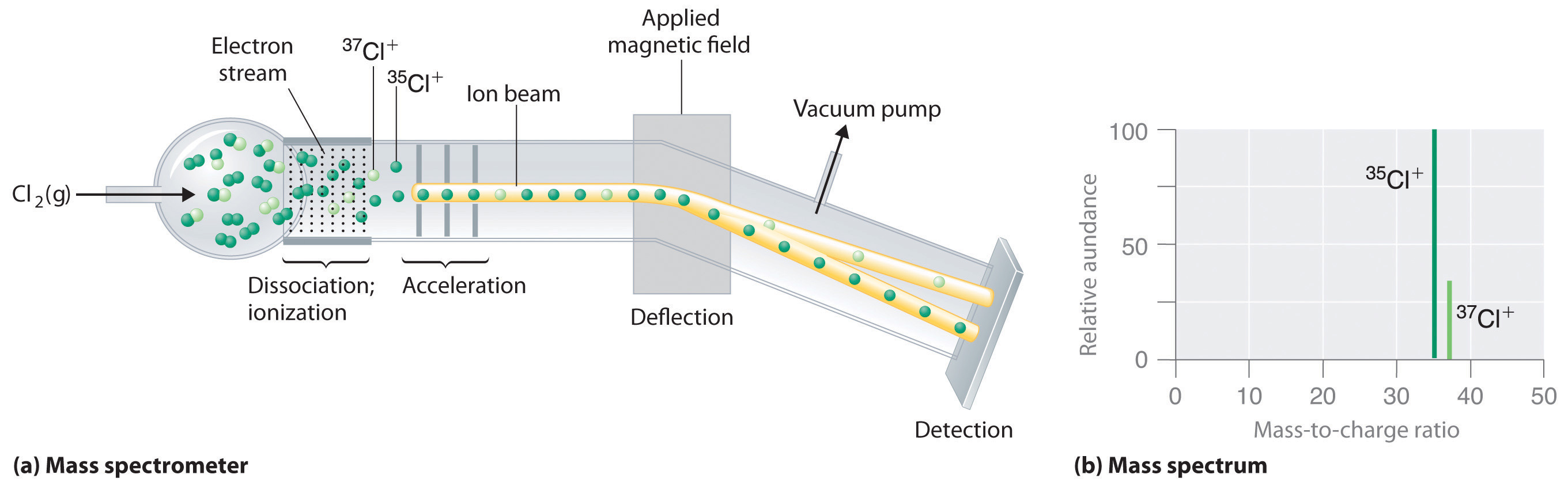
Below is a video from YouTube describing the mass spectrometer
Here is a bar chart showing the relative abundance of 4 isotopes of strontium
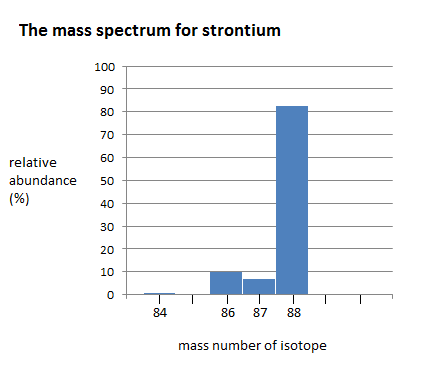
The mass spectrum of strontium has four different peaks, varying in intensity. The four peaks indicate that there are four isotopes of strontium. The four isotopes of strontium have isotopic mass numbers of 84, 86, 87, and 88, and relative abundances of 0.56%, 9.86%, 7.00%, and 82.58%, respectively. The intensity of the peak corresponds to the abundance. \(^{84}Sr\) has the smallest peak, which corresponds to its relative abundance of 0.56%, whereas \(^{88}Sr\) has the largest peak, which corresponds to its relative abundance of 82.58%. This indicates that \(^{88}Sr\) is the isotope that occurs in highest amounts.
Exercise \(\PageIndex{2}\)
Nitrogen has two isotopes, the first isotope has a mass of 14.004amu, while the second isotope has a mass of 15.000 amu, which isotope has the greatest natural abundance? Tip, you need to look at the periodic table.- 14N
- 15N
- There are equal amounts.
- Not enough information provided.
- none of the above
- Answer
-
A)The average atomic weight is 14.007 amu which is much closer to 14 then 15, so 14 is the most abundant isotope. In the next section you will use this kind of data to calculate fractional abundances.
Isotopic Abundance Calculations
For elements with more than one isotope there are a variety of problems you need to be able to solve. You not only need to be able to calculate the average mass from the isotopic abundance and masses, but go backwards, using the atomic weight on the periodic table as the average atomic mass. Rewriting eq. 2.3.1 in terms of algebraic variables gives us a feel for the types of problems. Consider an element with two isotopes A & B, each having a mass of mA or mb and a mole fraction of XA or Xbb .
\[\underbrace{X_A}_{\text{fraction A }}\underbrace{(m_A)}_{\text{ mass A}} + \underbrace{X_B}_{\text{fraction B }}\underbrace{(m_B)}_{\text{ mass B}} = \underbrace{m_{ave}}_{\text{average mass}}\]
In general the equation for an element with [n] isotopes is:
\[\sum_{i=1}^{n}X_im_i=m_{ave}\]
Note, the equation for two isotopes has 5 unknowns, and you can get mave from the periodic table, so you need to be given three of the other variables to solve the equation (one equation can only be solved for one unknown). But there is another equation we can use to reduce the number of unknowns. That is the sum of the fractions equals 1
\[X_A + X_B=1\]
or in general
\[\sum_{i=1}^{n}X_i=1\]
In the following problem we look
you not only need to be able to calculate the average atomic mass, but also need to be use the average mass on the periodic table to work backwards and calculate percent
Example \(\PageIndex{1}\): Calculating Average Atomic Mass
What is the average atomic mass of Neon, given that it has 3 isotopes with the follow percent abundances;
20Ne = 19.992 amu (90.51%), 21Ne = 20.993 amu (0.27%), 22Ne = 21.991 amu.
What we know: since you know what the element is, you can solve this without doing any math by using the periodic table, but you need to be able to do the math because it might be an unknown, and that is the only way you can Figure out the correct significant Figures.
Since Ne-20 has the greatest percent abundance, it should have the most impact on your average. Therefore, we expect the average atomic mass to be closer to the mass of Ne-20 (about 19.992 amu). Click the following video tutor to see if we estimated correctly.
Answer According to the correct number of significant Figures, we came up with 20.18 amu as the average atomic weight even though the average atomic weight from the periodic table is 20.179 amu. However, it is still a good check to make sure that you are on the right path.
Check Yourself: We predicted earlier that our answer should be closer to the mass of Ne-20 (19.992 amu) instead of Ne-21 or Ne-22 because it has the greatest natural abundance, and thus, impacts the average more. We can see that the math does align with our logic!
Example \(\PageIndex{1}\): Isotopic Mass Calculation
Chlorine has two isotopes, with 75.53% being 35Cl with an isotopic mass of 34.969 amu, what is the mass of the other isotope?
What we know: In this case, you have the average atomic mass (from the periodic table). You are trying to find the mass of the individual isotope. You also know that the individual isotopes have to add up to 100%.
Answer: The correct answer is 36.9 amu.
After watching the following two YouTubes, you should do the following worksheets, which were designed as in class activities for the prep course, and so give more step-by-step instructions than we are using. You will want to be able to bypass many of the "steps" in the handouts as these were designed for the preparatory chem 1300 class, which spent more time on this material. Also, note the handouts are posted as PDF files, and you can use the hypothes.is annotation system to comment on them, and if you tag them with the tag f19c1402c2, they will appear on the table of contents for this Chapter.
Isotope Abundance Worksheets:
Vocabulary
Test Yourself
Query \(\PageIndex{1}\)
Contributors and Attributions
Robert E. Belford (University of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert E. Belford, rebelford@ualr.edu. You should contact him if you have any concerns. This material has both original contributions, and content built upon prior contributions of the LibreTexts Community and other resources, including but not limited to:
- Anonymous
- Ronia Kattoum & November Palmer (UA Little Rock)
- Elena Lisitsyna (H5P interactive modules)


