10.1: Gas Properties
- Page ID
- 52147
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
In section 1.3 we introduced the phases of matter and in section 5.3 we covered phase transitions from a thermodynamic perspective. In this Chapter we will take a deeper look into the gas phase. We will start with covering basic gas properties and then learn several "equations of state", which are mathematical equations that relate measurable values like the volume, pressure and temperature of a gas to the quantity of particles (n) in the gas. We will apply these to gas phase stoichiometry, describe multi-component gases as homogenous mixtures (solutions), cover the kinetic molecular theory, which describes an ideal gas, and how real gases can deviate from it. We will also look at gases as dispersed particulate systems and cover properties like effusion and diffusion.
Characteristics of Gases
- Fluid - A gas is a fluid and will take the shape of a container it fills. There is zero viscosity (resistance to flow) and it fills the entire container.
- Compressible - The density of a gas changes as its volume changes. Thus, unlike incompressible solids or liquids, density alone can not be used to help identify a gas. That is, liquid water has a density of 1g/ml at normal temperature and pressure, and so that can be used to help identify a substance as water. But gaseous water (water vapor) fills a container, its density depends on the size of the container.
- Gases Form Solutions - Gas forms homogenous mixtures. Note, for liquid phase solutions we often identify a solvent and a solute, where the solute is dissolved in the solvent to form a solution. We usually consider the solvent to be the substance in greatest quantity, and an aqueous solution is one where water is the solvent. This is because the "space" of matter is being occupied by the liquid particles (which is why they are incompressible). In the gas phase, most of the "space" of matter is the "void" (which is why gasses are compressible), and so it is not normal to consider gas phase solutions to have a solute and solvent. Instead we use the concept of mole fraction to identify the relative proportions of different species in a gas mixture.
Measuring Gases: State Variables
State Variables - an equation of state relates measurable state variables to the number of gas particles. The Ideal Gas Law (PV=nRT) is an equation of state that relates the measurable state variables of Pressure, Temperature and Volume to the number of particles. There are other equations of state and we will discuss some at the end of the Chapter, but this course will expect a mastery of the ideal gas equation of state.
PV=nRT
P=Pressure, V=Volume, n=moles, T=Temperature (Kelvin)
R=0.08206(l-atm/mol-K) = 8.314J/(mol-K)
Pressure
Pressure is defined as force per unit area, \[P=\frac{F}{A}\] and the SI unit is the Pascal.
\[Pa=\frac{1N}{m^{2}}=\frac{1kg}{m\cdot s^{2}}\]
Note, the above definition if founded on the SI base units (kg, s and m) and since May of 2019 these have been defined by the 7 defined constants of nature (section 1B.3.1.2), with the relevant units being the Cs hyperfine transition frequency (atomic clock), speed of light in a vacuum and Boltzmann's constant. Of course we will use more practical definitions here, and the important thing to note is any measurable quantity can be traced back to the 7 SI Base units
This pressure of a gas can be understood by visualizing gas particles in constant motion, as exemplified in Figure \(\PageIndex{1}\).
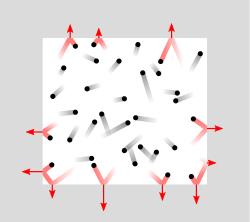
Figure \(\PageIndex{1}\): Gas particles in a sealed container. As the gas particles move they eventually hit the surface and impart a force on the surface as they change their direction of motion (red particles). The pressure is this force per unit area due to these collisions, which in SI units is the Pa (1N/m2).
It is more common to see pressure described in atm or torr (mm Hg), which are the units we will predominantly use in this class, and have macroscopic definitions that are more easily measured. Table 10.1.1 shows the common units of pressure, and their conversion factors.
| 1 atm = | 760 torr |
| 1 atm = | 760 mm Hg |
| 1 atm = | 14.7 lb/in2 |
| 1 atm = | 101,325 Pa |
Note, because all values in table \(\PageIndex{1}\) are set to one atmosphere, you can go directly between the other units (14.7 lb/in2 = 1.01x105 Pa = 760 torr...)
Atmosphere (unit)
One atmosphere of pressure is roughly the pressure felt at sea level by earth's atmosphere, as is shown in Figure \(\PageIndex{1}\). Note, this is not an easily reproducible value because the force felt on the earth changes over both your location and time. This YouTube from the National Naval Aviation Museum does a good job of showing how the air pressure changes as a function of altitude. That is, at the top of Mt Everest (about 5.5 miles high) there is a smaller column of air above you and so the pressure is less than at sea level, while in the Salton Sea CA (-228 ft) the pressure is higher than at sea level.
But also, because the atmosphere of the earth is really a mixture of gasses (mostly nitrogen and oxygen), with many species like water vapor, carbon dioxide, and air pollutants varying over time, so the mass of the column changes over time. So although the concept of an atmosphere of pressure is easy to understand, and it is important because reactions that occur on the surface of the earth occur at around one atmosphere of pressure, its variance over time and location makes it impractical to develop a scale on.
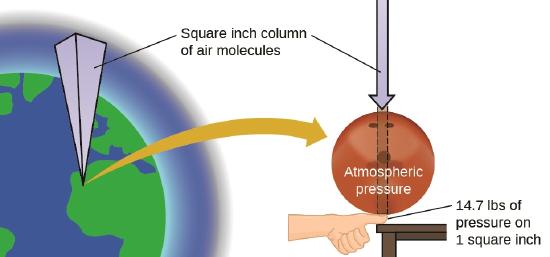
Figure \(\PageIndex{2}\): This image illustrates the concept of an atmosphere of pressure, which is the pressure felt at sea level due to the column of earth's atmosphere.
Video \(\PageIndex{1}\): YouTube from State Climate Office of NC demonstrating how the force of atmospheric pressure can collapse an empty can.https://youtu.be/QVayky_b-6U
In the above video, water vapor displaced the air when the water was boiled on the hotplate. It was then inverted and placed in an ice bath such that the opening was under the water surface, this caused the water vapor to condense and a vacuum was formed since there was no way for air to enter, and so the pressure on the inside became less than on the outside, and at some point it became great enough to collapse the can.
Torr (unit)
The torr or mm Hg is a reproducible definition of pressure based on the height of a column of mercury, and can be used to make an instrument to measure atmospheric pressure, the barometer. Using the conversion factor of 1 atm = 760 mm Hg, we could calibrate the barometer in units of atm. This is illustrated in Figure 10.1.3, where the height of the mercury column is dependent on the atmospheric pressure. If the atmospheric pressure is one atm the column is exactly at 760 mm Hg (760 torr). On a humid day the pressure outside goes up and the system is no longer at equilibrium, which forces the mercury up the tube (greater than 760 torr) until they balance out. On an arid day it lowers until they balance out.
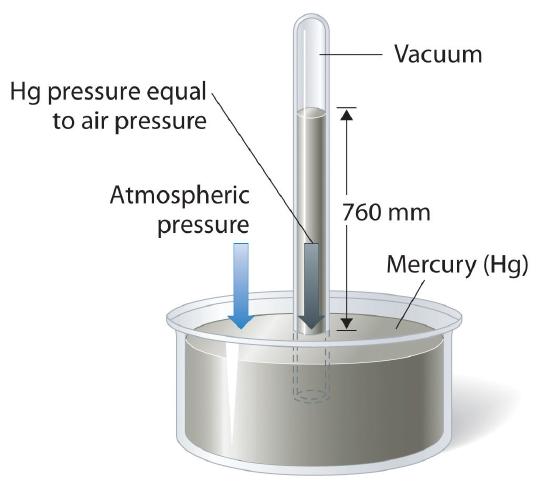
Figure \(\PageIndex{3}\): When at equilibrium the pressure due to the height of the column of mercury must equal the pressure due to the column of air.
Figure \(\PageIndex{3}\) gives a feel for how pressure can be measured. If the atmospheric pressure is higher than that due to the column of mercury it will push the column up until they are equal, if it is less, the column of mercury will go down until they are equal. For this to work, the mercury must be an incompressible fluid so that the mass of mercury in the column is proportional to the height of the column.
The following video from the North Carolina School of Science and Mathematics (NCSSM) shows how to make a mercury barometer.
Exercise \(\PageIndex{1}\)
Why do you think the column of mercury is 744 mm Hg in the above youtube from NCSSM?
- Answer
-
Obviously NCSSM is above sea level, but on closer look, it is in Durham NC, which is only 400 feet above sea level, and so it was also probably an arid day.
How could you measure the pressure of a gas in a sealed container?
A manometer is similar to a barometer, but allows you to measure the pressure of a gas in a sealed container.
Manometer
The manometer is the device that can measure the pressure of a gas in a closed container. There are two types of manometers, open ended and closed ended. Figure \(\PageIndex{4}\) shows the two basic types of manometers. The principle is that if the gas pressure on the left and right side of the manometer are not equal, the system will adjust until they are equal.
Figure \(\PageIndex{4}\): Closed (left) and open (middle and right) manometers. If the fluid is mercury, it reads directly in mmHg (or Torr).
Closed Barometer: In the closed barometer you are pushing the gas against a column of mercury where the opposite end is in a vacuum, and so the column of of fluid goes up until the pressure due to the column equals the pressure of the gas, and if the fluid is mercury, this is the pressure in mm Hg (torr).
Open Barometer: For the open barometer there are three options. The gas is less than, equal to, or greater than the atmosphere. If the gas pressure equals atmospheric pressure there is no difference in the heights of the columns.
- Gas Pressure < Atmospheric Pressure
\[P_{gas} + h = P_{atm}\]
The middle manometer in Figure \(\PageIndex{4}\) shows this case and since the atm pressure is greater it moves the mercury in towards the gas container until the forces cancel out.
- Gas Pressure > Atmospheric Pressure
\[P_{gas} = P_{atm} + h\]
The right manometer in Figure \(\PageIndex{4}\) shows the case where the gas pressure is greater, and so it pushes the mercury back against to atmosphere until the forces balance out.
Mercury is a common fluid because it is dense and so the height of the column is managable and can be described in units of mm (mm Hg to be exact), which is one definition of a unit of pressure. The same principle works for any incompressible fluid, where the pressure in Pascal is given by \(\rho\)gh, where \(\rho\) is the density, g is the gravitational constant (9.81 m/s2) and h is the height of the column.
Exercise \(\PageIndex{2}\)
Show that 760.0 mm Hg is approximately 101,325 Pa, given the density of mercury is 13.6g/ml and g= 9.81m/s2
- Answer
-
Solution: For mercury, \(\rho\) = 13.6g/cm3 and P=\(\rho\)gh. Pleae note, physics is not a prerequisite for this course and we have not gone over gravitational forces, but you should be able to do this problem based on two things. First you were given the equation and so should be able to substitute in the values, and second, you know the Pa is the SI unit, and can be expressed in terms of the 7 SI base units, which for this problem were the kg (mass), m (length) and time (s). So all you have to do is convert the units to the SI base units, and you have the value in Pa.
\[P=\rho gh=13.6\frac{g}{cm^{3}}\left (9.81\frac{m}{s^{2}} \right )760mm\left ( \frac{kg}{1000g} \right ) \left ( \frac{100cm}{m} \right )^3\left ( \frac{1m}{1000mm} \right )=101,396\frac{kg}{m\cdot s^{2}}=101,000Pa\]
Note g only had three significant digits.


