2.4: Units of Measurement

Metrology

Metrology is the science of measurement. There are two fundamental tenants to metrology; traceability and uncertainty.  Traceability is the ability to relate a measurement to a standard and uncertainty deals with how certain you are in the measurement based on the practice and technique you use to make the measurement. A thorough coverage of units and metrology is given in the Chem 1402 General chemistry 1 section on Units of Measurement. 

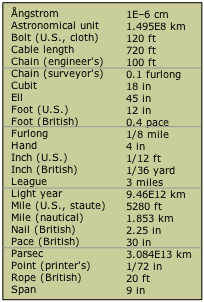
Lets start with something we are all familiar with, like the units of length (figure \(\PageIndex{1}\)).  Some are very small compared to others and we would choose a scale that is relevant to the magnitude of the entity we are measuring, like a map would relate distance from Little Rock to Memphis miles and not inches, but you would probably not want to know the length of your hand in miles. 

Figure \(\PageIndex{1}\): On the left are some of the units to describe length, some of which were based on human body parts (foot) or actions (pace).

The earliest units were based on artifacts, some of which were human body parts (foot) or action (pace). So if a king decreed that his foot was the standard of length, then someone could make a standard by marking an object by the length of the king's foot and use that object to measure other objects. But what happens if the king dies and the new king's foot is longer or shorter than the old kings? In fact, it is worst than that, as the king's foot can change in length, depending on how old he is, how he stands, etc. 

Today science uses what we commonly call the metric system. In fact most countries in the world use the metric system as the normal units of measurement.

Figure \(\PageIndex{2}\): Areas of the world using the metric system.

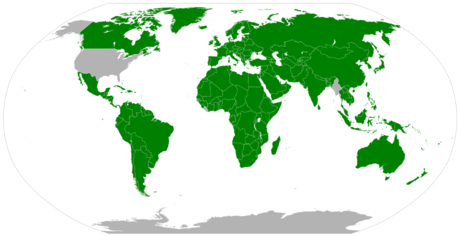
The customary units of measurement in the US are the foot, inch and pound, even though most of the rest of the world uses the metric system, as does the scientific community. The metric system has evolved over the years and today science uses the Système international d'unités (SI) units of measurement, which are far more complicated than the original metric units, and there are 7 fundamental SI base units that all matter can be represented under.  To give a feel for the magnitude of the challenges involved the base units of the SI system underwent a change on May 20, 2019, and are now based on defined numbers, the 7 fundamental constants of nature.  The details of these definitions are above the level of this class, in fact they are above the level of the typical general chemistry class, but if you are interested you may want to peruse through the section 1B.1.3.1.2 of the gen chem 1 LibreText.

Figure \(\PageIndex{2}\): On the left is an image of the old standard kilogram (credit: BIPM), and on the right are the 7 defined constants that are considered as "invariants of nature" and thus are numbers (credit: Stoughton/NIST).  How these are implemented are above the level of this course, and what is important is that students realize that as science advances, the most fundamental concepts as the values of the units of measurement evolve.

 

SI Base Units

The seven SI base units are listed in Table \(\PageIndex{1}\). These can be combined to form derived units that describe any measurable physical quantity. Thus by defining these seven SI base units, any physical measurement can be reproduced. In this class we will use the first five units extensively; the meter, kilogram, second, kelvin and mole (and general chemistry 2 will also use the ampere).

Table \(\PageIndex{1}\): Seven SI Base Units. Chem 1300 students need to know the units in red.

length	meter	m
mass	kilogram	kg
time	second	s
temperature (absolute)	kelvin	K
amount of substance	mole	mol
electric current	ampere	A
luminous intensity	candela	cd

Note, the SI unit for mass is the kilogram, represents 1,000 grams, and uses the si prefix kilo, which we will cover in section 2.7 (SI Prefixes).

Derived SI Units

As state above, any measurable phenomena can be described in terms of the SI base units.  There are two types of described units; those that are combinations of base units, like m²for area, and those with their own unit symbols, like Joules (J) for energy.

\[\underbrace{1J=1\frac{kg\cdot m^{2}}{s^{2}}}_{\text{SI Derived Unit of Energy in terms of SI Base Units}} \]

 

Table \(\PageIndex{2}\) shows common derived SI units:

Table \(\PageIndex{2}\): Derivied SI units and their dependencies on the SI bas units.

Quantity	Unit	Explanation
Work	N	Newton = kg m s^-2
Pressure	Pa	Pascal = N m^-2
Energy	J	Joule = N.m
Charge	C	Coulomb = A.s
Electric Potential	V	Volt = J/C
Power	Watt	1 watt = 1 J/s
Volume	L	1L = 1dm^3
Volume	mL	1mL = 1cm^3
Molarity	M	mol/L

Note, there are many non-SI units like the calorie, atm, foot, etc., which can also be described in terms of the SI base units. Conversions between units is covered in section 1B.3.5.