7.1: Stability of Conjugated Dienes- Molecular Orbital Theory

Conjugated vs. Non-conjugated Dienes

Dienes are compounds which contain two double bonds. These dienes can be non-conjugated (the two double bonds are separated by at least one sp³ hybridized atom. Conjugated dienes have the two double bonds separated by a single bond. Conjugated dienes have properties and reactivity which are distinctly different than non-conjugated dienes. Determining if double bonds are conjugated represents an important skill in organic chemistry.

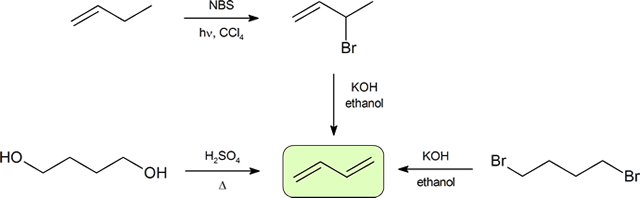
Synthesis of Dienes

Conjugated dienes can be prepared using many of the methods used for the preparation of alkenes previously discussed (Sections 11-7, 11-8, 11-9, and 11-10). A convenient method starts with the free radical halogenation of the allylic carbon of an alkene using NBS. The resulting halide can then be reacted with a strong base to result in E2 elimination and create a diene product. The compound, 1,3-butadiene, is the simplest conjugated diene and has an important use in the synthesis of polymers. Many simple dienes, such as 1,3-butadiene and isoprene, can be prepared industrially by the double dehydration of alcohols and the double dehydrohalogenation of organohalides.

Stability of Conjugated Dienes

Conjugated dienes are known to be more stable than non-conjugated dienes as shown by their experimentally determined heats of hydrogenation. It has been shown that as alkenes become more stable, they contain less energy, and therefore release less heat during hydrogenation. Experiments have shown that conjugated dienes have a lower heat of hydrogenation (-226 kJ/mol) than non-conjugated dienes (-251 kJ/mol). Using the differences in heats of hydrogenation the stabilization energy in conjugated dienes can be estimate to be roughly 25 kJ/mol.

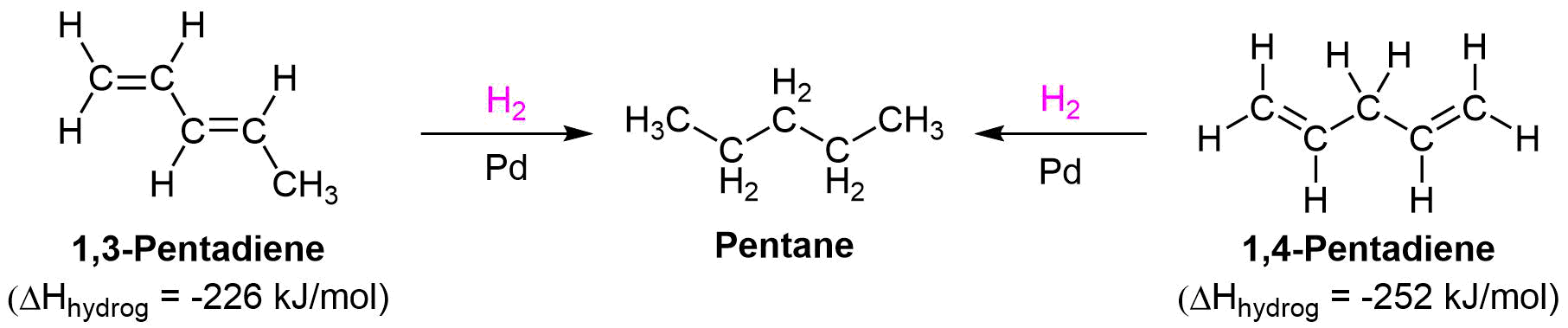
Here is an energy diagram comparing different types of bonds with their heats of hydrogenation to show relative stability of each molecule:

The stabilization of dienes by conjugation is less dramatic than the aromatic stabilization of benzene. Nevertheless, similar resonance and molecular orbital descriptions of conjugation may be written.

Each alkene carbon in 1,3 dienes are sp² hybridized and therefore have one unhybridized p orbital. The four p orbitals in 1,3-butadiene overlap to form a conjugated system which can be represented by the resonance forms shown below. This delocalization of charges stabilizes conjugated diene making them more stable than non-conjugated dienes.

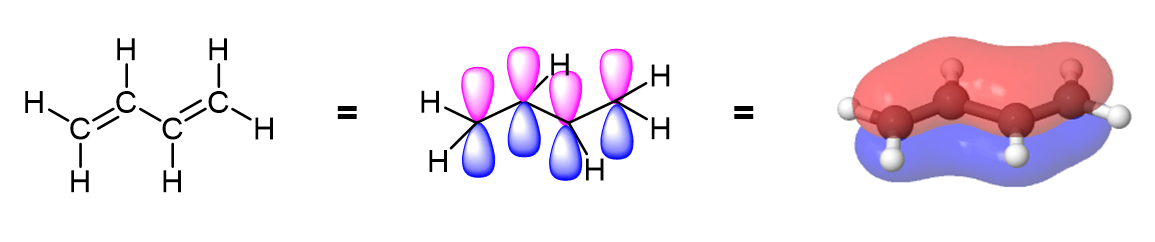
Evidence of conjugation in 1,3 dienes is seen in the single bond being stronger and shorter (147 pm) than an ordinary alkane C-C bond (154 pm). The resonance hybrid of a 1,3-butadiene shows this bond to contain significant double bond character with its bond length being roughly the average of a single and double bond.

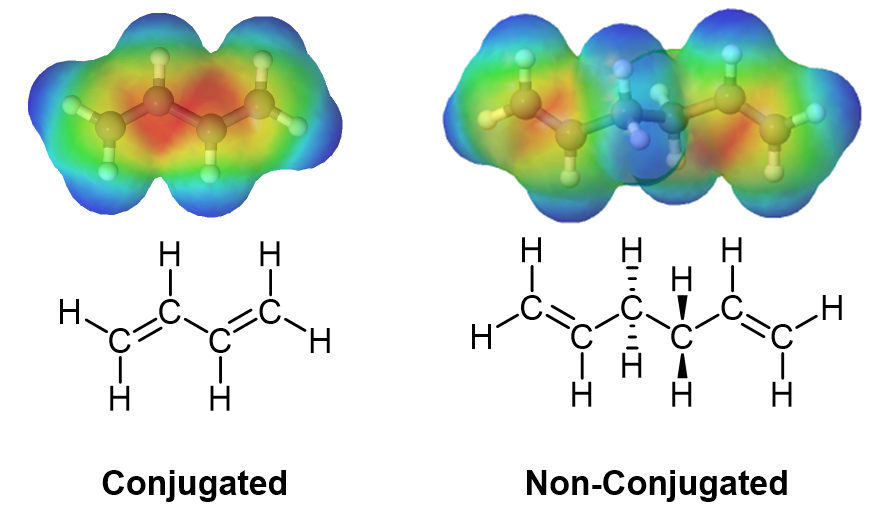
The delocalized electron density of a 1,3 diene can be seen when viewing an electrostatic potential maps. In conjugated dienes, it is observed that the pi electron density overlap (shown in red) is closer together and delocalized in conjugated dienes, while in non-conjugated dienes the pi electron density is located completely on the double bonds.

Experimental Evidence for Conjugation

One useful way to test for the presence of conjugation is to expose the pi system to light in the UV to Visible range of the electromagnetic spectrum. Conjugated pi systems absorb photons of lower wavelengths, meaning less energetic photons are absorbed as the length of the conjugated system increases.

 This effect is best explained using Molecular Orbital theory, which can be used to show that the increased degree of conjugation produces a smaller gap between the pi and pi* orbitals between which the electrons transition when absorbing light in the UV-Vis spectrum. For now, it is enough to recognize that conjugation can be detected using UV-Vis spectroscopy.

 

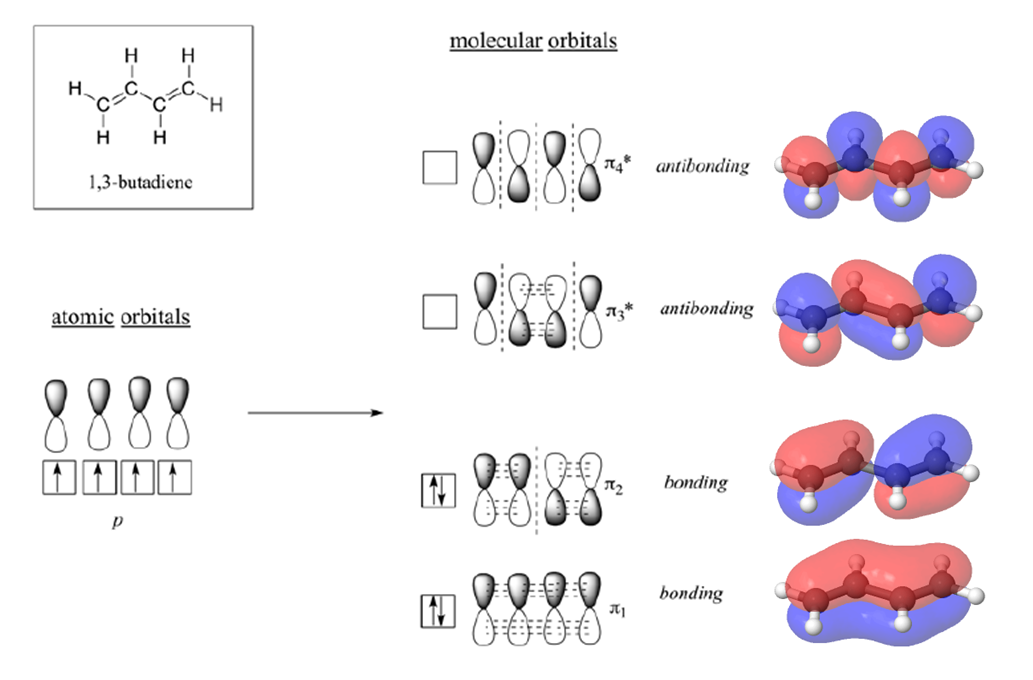
Molecular Orbitals of 1,3 Dienes

According to MO theory discussed in section 1-11, when a double bond is non-conjugated, the two atomic 2p_z orbitals combine to form two pi (π) molecular orbitals, one a low-energy π bonding orbital and one a high-energy π-star (π*) anti-bonding molecular orbital. These are sometimes denoted, in MO diagrams like the one below, with the Greek letter psi (Ψ) instead of π. In the bonding Ψ₁ orbital, the two (+) lobes of the 2p_z orbitals interact constructively with each other, as do the two (-) lobes. Therefore, there is increased electron density between the nuclei in the molecular orbital – this is why it is a bonding orbital. In the higher-energy anti-bonding Ψ₂* orbital, the (+) lobes of one 2p_z orbital interacts destructively with the (-) lobe of the second 2p_z orbital, leading to a node between the two nuclei and overall repulsion. By the aufbau principle, the two electrons from the two atomic orbitals will be paired in the lower-energy Ψ₁orbital when the molecule is in the ground state.

With a conjugated diene, such as 1,3-butadiene, the four 2p atomic orbitals combine to form four pi molecular orbitals of increasing energy. Two bonding pi orbitals and two anti-bonding pi* orbitals. The combination of four pi molecular orbitals allow for the formation of a bonding molecular orbital that is lower in energy than those created by an unconjugated alkene. The 4 pi electrons of 1,3-butadiene completely fill the bonding molecular orbitals giving is the additional stability associated with conjugated double bonds.