1.11: Describing Chemical Bonds - Molecular Orbital Theory
- Page ID
- 31378
After completing this section, you should be able to
- describe the formation of covalent bonds in terms of molecular orbitals.
- account for differences in bond length and strength in terms of the efficiency with which atomic orbitals overlap.
- draw simple molecular orbital diagrams (e.g., for the H2 molecule) showing the formation of bonding and anti-bonding orbitals.
Make certain that you can define, and use in context, the key terms below.
- anti-bonding molecular orbital
- bonding molecular orbital
- molecular orbital (MO) theory
As we have seen, valence bond theory does a remarkably good job of explaining the bonding geometry and properties of many organic compounds. There are some areas, however, where the valence bond theory falls short. It fails to adequately account, for example, for some interesting properties of compounds that contain alternating double and single bonds. In order to understand these properties, we need to think about chemical bonding in a new way, using the ideas of molecular orbital (MO) theory.
Another look at the H2 molecule: bonding and anti-bonding sigma molecular orbitals
Let’s consider again the simplest possible covalent bond: the one in molecular hydrogen (H2). When we described the hydrogen molecule using valence bond theory, we said that the two 1s orbitals from each atom overlap, allowing the two electrons to be shared and thus forming a covalent bond. In molecular orbital theory, we make a further statement: we say that the two atomic 1s orbitals don’t just overlap, they actually combine to form two completely new orbitals. These two new orbitals, instead of describing the likely location of an electron around a single nucleus, describe the location of an electron pair around two or more nuclei. The bonding in H2, then, is due to the formation of a new molecular orbital (MO), in which a pair of electrons is delocalized around two hydrogen nuclei.
An important principle of quantum mechanical theory is that when orbitals combine, the number of orbitals before the combination takes place must equal the number of new orbitals that result – orbitals don’t just disappear! We saw this previously when we discussed hybrid orbitals: one s and three p orbitals make four sp3 hybrids. When two atomic 1s orbitals combine in the formation of H2, the result is two molecular orbitals called sigma (σ) orbitals. According to MO theory, the first sigma orbital is lower in energy than either of the two isolated atomic 1s orbitals – thus this sigma orbital is referred to as a bonding molecular orbital. The second, sigma-star (σ*) orbital is higher in energy than the two atomic 1s orbitals, and is referred to as an anti-bonding molecular orbital. In MO theory, a star (*) sign always indicates an anti-bonding orbital.

Following the aufbau ('building up') principle, we place the two electrons in the H2 molecule in the lowest energy molecular orbital, which is the (bonding) sigma orbital.
The bonding sigma orbital, which holds both electrons in the ground state of the molecule, is egg-shaped, encompassing the two nuclei, and with the highest likelihood of electrons being in the area between the two nuclei. The high-energy, anti-bonding sigma-star orbital can be visualized as a pair of droplets, with areas of higher electron density near each nucleus and a ‘node’, (area of zero electron density) midway between the two nuclei.
Remember that we are thinking here about electron behavior as wave behavior. When two separate waves combine, they can do so with what is called constructive interference, where the two amplitudes reinforce one another, or destructive interference, where the two amplitudes cancel one another out. Bonding MO’s are the consequence of constructive interference between two atomic orbitals which results in an attractive interaction and an increase in electron density between the nuclei. Anti-bonding MO’s are the consequence of destructive interference which results in a repulsive interaction and a ‘canceling out’ of electron density between the nuclei (in other words, a node).
MO theory and pi bonds
In p orbitals, the wave function gives rise to two lobes with opposite phases, analogous to how a two-dimensional wave has both parts above and below the average. We indicate the phases by shading the orbital lobes different colors. When orbital lobes of the same phase overlap, constructive wave interference increases the electron density. When regions of opposite phase overlap, the destructive wave interference decreases electron density and creates nodes. When p orbitals overlap end to end, they create σ and σ* orbitals. If two atoms are located along the x-axis in a Cartesian coordinate system, the two px orbitals overlap end to end and form σpx (bonding) and σ∗px (antibonding) (read as "sigma-p-x" and "sigma-p-x star," respectively). Just as with s-orbital overlap, the asterisk indicates the orbital with a node between the nuclei, which is a higher-energy, antibonding orbital.
The advantage of MO theory becomes more apparent when we think about pi bonds, especially in those situations where two or more pi bonds are able to interact with one another. Let’s first consider the pi bond in ethene from an MO theory standpoint (in this example we will be disregarding the various sigma bonds, and thinking only about the pi bond). According to MO theory, the two atomic 2pz orbitals combine to form two pi (π) molecular orbitals, one a low-energy π bonding orbital and one a high-energy π-star (π*) anti-bonding molecular orbital. These are sometimes denoted, in MO diagrams like the one below, with the Greek letter psi (Ψ) instead of π.
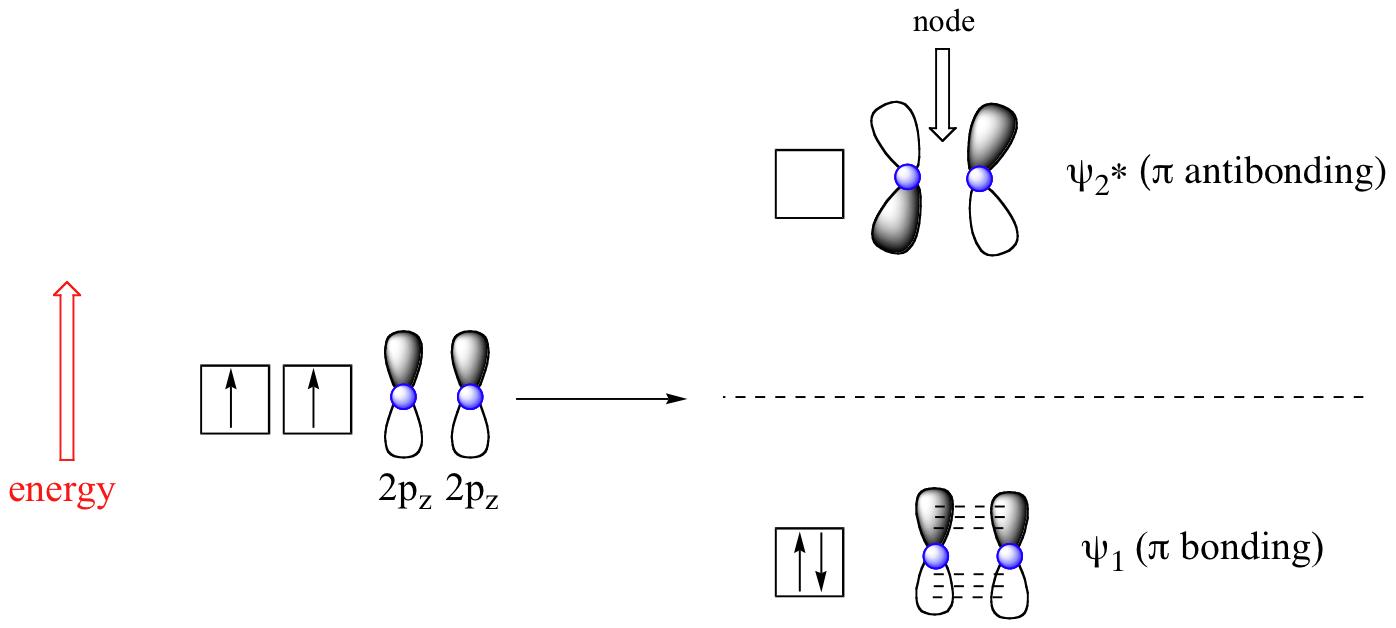
In the bonding Ψ1 orbital, the two shaded lobes of the 2pz orbitals interact constructively with each other, as do the two unshaded lobes (remember, the shading choice represents mathematical (+) and (-) signs for the wavefunction). Therefore, there is increased electron density between the nuclei in the molecular orbital – this is why it is a bonding orbital.
In the higher-energy anti-bonding Ψ2* orbital, the shaded lobe of one 2pz orbital interacts destructively with the unshaded lobe of the second 2pz orbital, leading to a node between the two nuclei and overall repulsion. By the aufbau principle, the two electrons from the two atomic orbitals will be paired in the lower-energy Ψ1 orbital when the molecule is in the ground state.
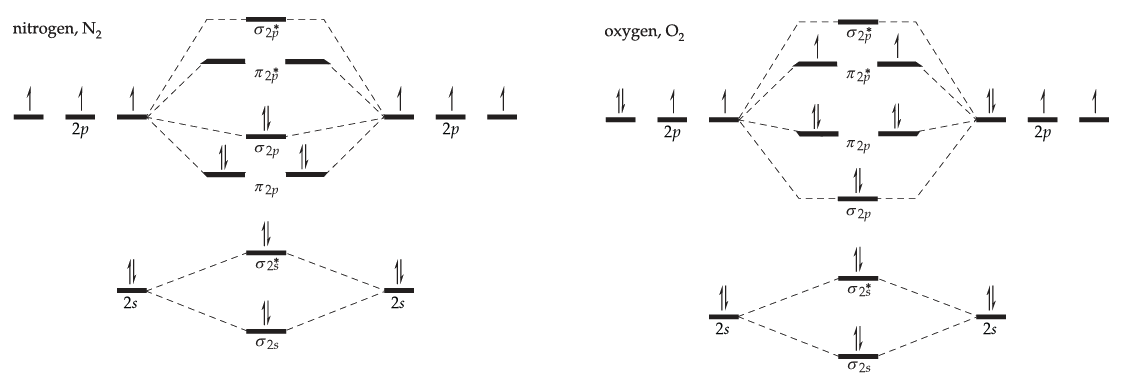
Draw a simple molecular orbital diagram for each of the following molecules
- nitrogen, N2.
- oxygen, O2.
Solution