7.1: Acid-Base Buffers

Last updated
Save as PDF

Page ID: 393584

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Skills to Develop

Describe the composition and function of acid–base buffers
Calculate the pH of a buffer before and after the addition of added acid or base using the Henderson-Hasselbalch approximation

A mixture of a weak acid and its conjugate base (or a mixture of a weak base and its conjugate acid) is called a buffer solution, or a buffer. Buffer solutions resist a change in pH when small amounts of a strong acid or a strong base are added (Figure \(\PageIndex{1}\)). A solution of acetic acid (\(\ce{CH3COOH}\) and sodium acetate \(\ce{CH3COONa}\)) is an example of a buffer that consists of a weak acid and its salt. An example of a buffer that consists of a weak base and its salt is a solution of ammonia (\(\ce{NH3(aq)}\)) and ammonium chloride (\(\ce{NH4Cl(aq)}\)).

Figure \(\PageIndex{1}\): (a) The unbuffered solution on the left and the buffered solution on the right have the same pH (pH 8); they are basic, showing the yellow color of the indicator methyl orange at this pH. (b) After the addition of 1 mL of a 0.01-M HCl solution, the buffered solution has not detectably changed its pH but the unbuffered solution has become acidic, as indicated by the change in color of the methyl orange, which turns red at a pH of about 4. (credit: modification of work by Mark Ott)

How Buffers Work

In order for a buffer to "resist" the effect of adding strong acid or strong base, it must have both an acidic and a basic component. However, you cannot mix any two acid/base combination together and get a buffer. If you mix HCl and NaOH, for example, you will simply neutralize the acid with the base and obtain a neutral salt, not a buffer. For a buffer to work, both the acid and the base component must be part of the same equilibrium system - that way, neutralizing one or the other component (by adding strong acid or base) will transform it into the other component, and maintain the buffer mixture.

Therefore, a buffer must consist of a mixture of a weak conjugate acid-base pair.

The pH a buffer maintains is determined by the nature of the conjugate pair and the concentrations of both components. A mixture of acetic acid and sodium acetate is acidic because the K_a of acetic acid is greater than the K_b of its conjugate base acetate. It is a buffer because it contains both the weak acid and its salt. Hence, it acts to keep the hydronium ion concentration (and the pH) almost constant by the addition of either a small amount of a strong acid or a strong base. If we add a base such as sodium hydroxide, the hydroxide ions react with the few hydronium ions present. Then more of the acetic acid reacts with water, restoring the hydronium ion concentration almost to its original value:

\[\ce{CH3CO2H}(aq)+\ce{H2O}(l)⟶\ce{H3O+}(aq)+\ce{CH3CO2-}(aq)\]

The pH changes very little. If we add an acid such as hydrochloric acid, most of the hydronium ions from the hydrochloric acid combine with acetate ions, forming acetic acid molecules:

\[\ce{H3O+}(aq)+\ce{CH3CO2-}(aq)⟶\ce{CH3CO2H}(aq)+\ce{H2O}(l)\]

Thus, there is very little increase in the concentration of the hydronium ion, and the pH remains practically unchanged (Figure \(\PageIndex{2}\)).

Figure \(\PageIndex{2}\): This diagram shows the buffer action of these reactions.

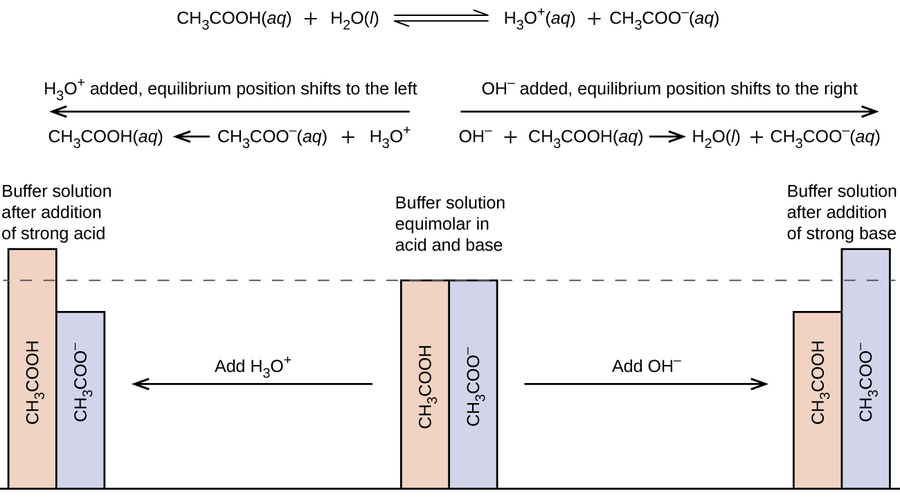
A mixture of ammonia and ammonium chloride is basic because the K_b for ammonia is greater than the K_a for the ammonium ion. It is a buffer because it also contains the salt of the weak base. If we add a base (hydroxide ions), ammonium ions in the buffer react with the hydroxide ions to form ammonia and water and reduce the hydroxide ion concentration almost to its original value:

\[\ce{NH4+}(aq)+\ce{OH-}(aq)⟶\ce{NH3}(aq)+\ce{H2O}(l)\]

If we add an acid (hydronium ions), ammonia molecules in the buffer mixture react with the hydronium ions to form ammonium ions and reduce the hydronium ion concentration almost to its original value:

\[\ce{H3O+}(aq)+\ce{NH3}(aq)⟶\ce{NH4+}(aq)+\ce{H2O}(l)\]

The three parts of the following example illustrate the change in pH that accompanies the addition of base to a buffered solution of a weak acid and to an unbuffered solution of a strong acid.

Example \(\PageIndex{1}\): pH Changes in Buffered and Unbuffered Solutions

Acetate buffers are used in biochemical studies of enzymes and other chemical components of cells to prevent pH changes that might change the biochemical activity of these compounds.

Calculate the pH of an acetate buffer that is a mixture with 0.10 M acetic acid and 0.10 M sodium acetate.
Calculate the pH after 1.0 mL of 0.10 M NaOH is added to 100 mL of this buffer, giving a solution with a volume of 101 mL.
For comparison, calculate the pH after 1.0 mL of 0.10 M NaOH is added to 100 mL of a solution of an unbuffered solution with a pH of 4.74 (e.g. a 1.8 × 10⁻⁵-M solution of HCl). The volume of the final solution is 101 mL.

Solution

Calculate the pH of an acetate buffer that is a mixture with 0.10 M acetic acid and 0.10 M sodium acetate.
To determine the pH of the buffer solution we use a typical equilibrium calculation (as illustrated in earlier Examples):
1. Determine the direction of change. The equilibrium in a mixture of H₃O⁺, \(\ce{CH3CO2-}\), and CH₃CO₂H is:
  
  \[\ce{CH3CO2H}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{CH3CO2-}(aq) \]
  
  The equilibrium constant for CH₃CO₂H is not given, so we look it up in Table E1: K_a = 1.8 × 10⁻⁵. With [CH₃CO₂H] = \(\ce{[CH3CO2- ]}\) = 0.10 M and [H₃O⁺] = ~0 M, the reaction shifts to the right to form H₃O⁺.
2. Determine x and equilibrium concentrations. A table of changes and concentrations follows:
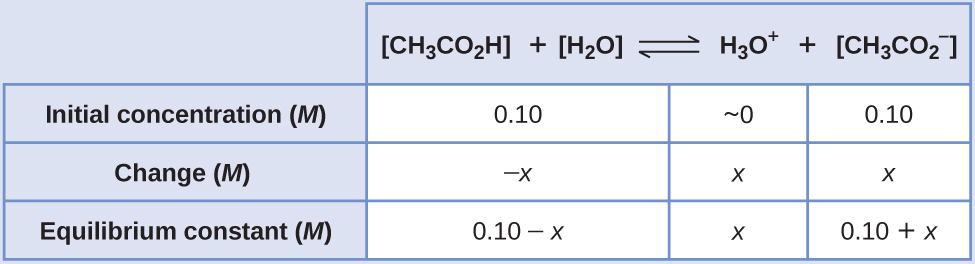
3. Solve for x and the equilibrium concentrations. We find:
  \[x=1.8×10^{−5}\:M\]

and

\[\ce{[H3O+]}=0+x=1.8×10^{−5}\:M\]

Thus:

\[\mathrm{pH=−log[H_3O^+]=−log(1.8×10^{−5})}\]

\[=4.74\]

4. Check the work. If we calculate all calculated equilibrium concentrations, we find that the equilibrium value of the reaction coefficient, Q = K_a.

(b) Calculate the pH after 1.0 mL of 0.10 M NaOH is added to 100 mL of this buffer, giving a solution with a volume of 101 mL.

First, we calculate the concentrations of an intermediate mixture resulting from the complete reaction between the acid in the buffer and the added base. Then we determine the concentrations of the mixture at the new equilibrium:

Determine the moles of NaOH. One milliliter (0.0010 L) of 0.10 M NaOH contains:
\[\mathrm{0.0010\cancel{L}×\left(\dfrac{0.10\:mol\: NaOH}{1\cancel{L}}\right)=1.0×10^{−4}\:mol\: NaOH} \]
Determine the moles of CH₃CO₂H. Before reaction, 0.100 L of the buffer solution contains:
\[\mathrm{0.100\cancel{L}×\left(\dfrac{0.100\:mol\:CH_3CO_2H}{1\cancel{L}}\right)=1.00×10^{−2}\:mol\:CH_3CO_2H} \]
Solve for the amount of NaCH₃CO₂ produced. The 1.0 × 10⁻⁴ mol of NaOH neutralizes 1.0 × 10⁻⁴ mol of CH₃CO₂H, leaving:

\[\mathrm{(1.0×10^{−2})−(0.01×10^{−2})=0.99×10^{−2}\:mol\:CH_3CO_2H} \]

and producing 1.0 × 10⁻⁴ mol of NaCH₃CO₂. This makes a total of:

[\mathrm{(1.0×10^{−2})+(0.01×10^{−2})=1.01×10^{−2}\:mol\:NaCH_3CO_2} \]

4. Find the molarity of the products. After reaction, CH₃CO₂H and NaCH₃CO₂ are contained in 101 mL of the intermediate solution, so:

\[\ce{[CH3CO2H]}=\mathrm{\dfrac{9.9×10^{−3}\:mol}{0.101\:L}}=0.098\:M \]

\[\ce{[NaCH3CO2]}=\mathrm{\dfrac{1.01×10^{−2}\:mol}{0.101\:L}}=0.100\:M \]

Now we calculate the pH after the intermediate solution, which is 0.098 M in CH₃CO₂H and 0.100 M in NaCH₃CO₂, comes to equilibrium. The calculation is very similar to that in part (a) of this example:

This series of calculations gives a pH = 4.75. Thus the addition of the base barely changes the pH of the solution.

(c) This 1.8 × 10⁻⁵-M solution of HCl has the same hydronium ion concentration as the 0.10-M solution of acetic acid-sodium acetate buffer described in part (a) of this example. The solution contains:

\(\mathrm{0.100\:L×\left(\dfrac{1.8×10^{−5}\:mol\: HCl}{1\:L}\right)=1.8×10^{−6}\:mol\: HCl} \)

As shown in part (b), 1 mL of 0.10 M NaOH contains 1.0 × 10⁻⁴ mol of NaOH. When the NaOH and HCl solutions are mixed, the HCl is the limiting reagent in the reaction. All of the HCl reacts, and the amount of NaOH that remains is:

\( (1.0×10^{−4})−(1.8×10^{−6})=9.8×10^{−5}\:M \)

The concentration of NaOH is:

\(\dfrac{9.8×10^{−5}\:M\:\ce{NaOH}}{0.101\:\ce{L}}=9.7×10^{−4}\:M \)

The pOH of this solution is:

\(\mathrm{pOH=−log[OH^- ]=−log(9.7×10^{−4})=3.01} \)

The pH is:

\(\mathrm{pH=14.00−pOH=10.99} \)

The pH changes from 4.74 to 10.99 in this unbuffered solution. This compares to the change of 4.74 to 4.75 that occurred when the same amount of NaOH was added to the buffered solution described in part (b).

Exercise \(\PageIndex{1}\)

Show that adding 1.0 mL of 0.10 M HCl changes the pH of 100 mL of a 1.8 × 10⁻⁵ M HCl solution from 4.74 to 3.00.

Answer

Initial pH of 1.8 × 10⁻⁵ M HCl; pH = −log[H₃O⁺] = −log[1.8 × 10⁻⁵] = 4.74

Moles of H₃O⁺ added by addition of 1.0 mL of 0.10 M HCl: 0.10 moles/L × 0.0010 L = 1.0 × 10⁻⁴ moles; final pH after addition of 1.0 mL of 0.10 M HCl:

\[\mathrm{pH=−log[H_3O^+]=−log\left(\dfrac{total\: moles\:H_3O^+}{total\: volume}\right)=−log\left(\dfrac{1.0×10^{−4}\:mol+1.8×10^{−6}\:mol}{101\:mL\left(\dfrac{1\:L}{1000\:mL}\right)}\right)=3.00} \]

The Henderson-Hasselbalch Approximation

We have seen in Example \(\PageIndex{1}\) how the pH of a buffer may be calculated using the ICE table method. The method requires knowing the concentrations of the conjugate acid-base pair and the \(K_a\) or \(K_b\) of the weak acid or weak base. However, there is a simpler method using the same information in a convenient formula, based on a rearrangement of the equilibrium equation for the dissociation of a weak acid.

The simplified ionization reaction of any weak acid is \(HA \leftrightharpoons H^+ + A^−\), for which the equilibrium constant expression is as follows:

\[K_a=\dfrac{[H^+][A^-]}{[HA]} \label{Eq5}\]

This equation can be rearranged as follows:

\[[H^+]=K_a\dfrac{[HA]}{[A^−]} \label{Eq6}\]

Taking the logarithm of both sides and multiplying both sides by −1,

\[ \begin{align} −\log[H^+] &=−\log K_a−\log\left(\dfrac{[HA]}{[A^−]}\right) \\[4pt] &=−\log{K_a}+\log\left(\dfrac{[A^−]}{[HA]}\right) \label{Eq7} \end{align}\]

Replacing the negative logarithms in Equation \(\ref{Eq7}\) to obtain pH, we get,

\[pH=pK_a+\log \left( \dfrac{[A^−]}{[HA]} \right) \label{Eq8}\]

or, more generally,

\[pH=pK_a+\log\left(\dfrac{[base]}{[acid]}\right) \label{Eq9}\]

Equation \(\ref{Eq8}\) and Equation \(\ref{Eq9}\) are both forms of the Henderson-Hasselbalch approximation, named after the two early 20th-century chemists who first noticed that this rearranged version of the equilibrium constant expression provides an easy way to calculate the pH of a buffer solution. In general, the validity of the Henderson-Hasselbalch approximation may be limited to solutions whose concentrations are at least 100 times greater than their \(K_a\) values (the "x is small" assumption).

There are three special cases where the Henderson-Hasselbalch approximation is easily interpreted without the need for calculations:

\([base] = [acid]\): Under these conditions, \[\dfrac{[base]}{[acid]} = 1\] in Equation \(\ref{Eq9}\). Because \(\log 1 = 0\), \[pH = pK_a\] regardless of the actual concentrations of the acid and base.
\([base]/[acid] = 10\): In Equation \(\ref{Eq9}\), because \(\log 10 = 1\), \[pH = pK_a + 1.\]
\([base]/[acid] = 100\): In Equation \(\ref{Eq9}\), because \(\log 100 = 2\), \[pH = pK_a + 2.\]

Each time we increase the [base]/[acid] ratio by 10, the pH of the solution increases by 1 pH unit. Conversely, if the [base]/[acid] ratio is 0.1, then pH = \(pK_a\) − 1. Each additional factor-of-10 decrease in the [base]/[acid] ratio causes the pH to decrease by 1 pH unit.

If [base] = [acid] for a buffer, then pH = \(pK_a\). Changing the ratio by a factor of 10 changes the pH by ±1 unit.

Example \(\PageIndex{2}\)

What is the pH of a solution that contains

0.135 M \(HCO_2H\) and 0.215 M \(HCO_2Na\)? (The \(pK_a\) of formic acid is 3.75.)
0.0135 M \(HCO_2H\) and 0.0215 M \(HCO_2Na\)?
0.119 M pyridine and 0.234 M pyridine hydrochloride? (The \(pK_b\) of pyridine is 8.77.)

Given: concentration of acid, conjugate base, and \(pK_a\); concentration of base, conjugate acid, and \(pK_b\)

Asked for: pH

Strategy:

Substitute values into either form of the Henderson-Hasselbalch approximation (Equation \(\ref{Eq8}\) or Equation \(\ref{Eq9}\)) to calculate the pH.

Solution:

According to the Henderson-Hasselbalch approximation (Equation \(\ref{Eq8}\)), the pH of a solution that contains both a weak acid and its conjugate base is

\[pH = pK_a + \log([A−]/[HA]).\]

Inserting the given values into the equation,

\[\begin{align*} pH &=3.75+\log\left(\dfrac{0.215}{0.135}\right) \\[4pt] &=3.75+\log 1.593 \\[4pt] &=3.95 \end{align*}\]

This result makes sense because the \([A^−]/[HA]\) ratio is between 1 and 10, so the pH of the buffer must be between the \(pK_a\) (3.75) and \(pK_a + 1\), or 4.75.

This is identical to part (a), except for the concentrations of the acid and the conjugate base, which are 10 times lower. Inserting the concentrations into the Henderson-Hasselbalch approximation,

\[\begin{align*} pH &=3.75+\log\left(\dfrac{0.0215}{0.0135}\right) \\[4pt] &=3.75+\log 1.593 \\[4pt] &=3.95 \end{align*}\]

This result is identical to the result in part (a), which emphasizes the point that the pH of a buffer depends only on the ratio of the concentrations of the conjugate base and the acid, not on the magnitude of the concentrations. Because the [A⁻]/[HA] ratio is the same as in part (a), the pH of the buffer must also be the same (3.95).

In this case, we have a weak base, pyridine (Py), and its conjugate acid, the pyridinium ion (\(HPy^+\)). We will therefore use Equation \(\ref{Eq9}\), the more general form of the Henderson-Hasselbalch approximation, in which “base” and “acid” refer to the appropriate species of the conjugate acid–base pair. We are given [base] = [Py] = 0.119 M and \([acid] = [HPy^{+}] = 0.234\, M\). We also are given \(pK_b = 8.77\) for pyridine, but we need \(pK_a\) for the pyridinium ion. Recall that the \(pK_b\) of a weak base and the \(pK_a\) of its conjugate acid are related:

\[pK_a + pK_b = pK_w.\]

Thus \(pK_a\) for the pyridinium ion is \(pK_w − pK_b = 14.00 − 8.77 = 5.23\). Substituting this \(pK_a\) value into the Henderson-Hasselbalch approximation,

\[\begin{align*} pH=pK_a+\log \left(\dfrac{[base]}{[acid]}\right) \\[4pt] &=5.23+\log\left(\dfrac{0.119}{0.234}\right) \\[4pt] & =5.23 −0.294 \\[4pt] &=4.94 \end{align*}\]

Once again, this result makes sense: the \([B]/[BH^+]\) ratio is about 1/2, which is between 1 and 0.1, so the final pH must be between the \(pK_a\) (5.23) and \(pK_a − 1\), or 4.23.

Exercise \(\PageIndex{2}\)

What is the pH of a solution that contains

0.333 M benzoic acid and 0.252 M sodium benzoate?
0.050 M trimethylamine and 0.066 M trimethylamine hydrochloride?

The \(pK_a\) of benzoic acid is 4.20, and the \(pK_b\) of trimethylamine is also 4.20.

Answer a: 4.08
Answer b: 9.68

The Henderson-Hasselbalch approximation ((Equation \(\ref{Eq8}\)) can also be used to calculate the pH of a buffer solution after adding a given amount of strong acid or strong base, as demonstrated in Example \(\PageIndex{3}\).

Example \(\PageIndex{3}\)

The buffer solution in Example \(\PageIndex{2}\) contained 0.135 M \(HCO_2H\) and 0.215 M \(HCO_2Na\) and had a pH of 3.95.

What is the final pH if 5.00 mL of 1.00 M \(HCl\) are added to 100 mL of this solution?
What is the final pH if 5.00 mL of 1.00 M \(NaOH\) are added?

Given: composition and pH of buffer; concentration and volume of added acid or base

Asked for: final pH

Strategy:

Calculate the amounts of formic acid and formate present in the buffer solution. Then calculate the amount of acid or base added.
Construct a table showing the amounts of all species after the neutralization reaction. Use the final volume of the solution to calculate the concentrations of all species. Finally, substitute the appropriate values into the Henderson-Hasselbalch approximation (Equation \(\ref{Eq9}\)) to obtain the pH.

Solution:

The added \(HCl\) (a strong acid) or \(NaOH\) (a strong base) will react completely with formate (a weak base) or formic acid (a weak acid), respectively, to give formic acid or formate and water. We must therefore calculate the amounts of formic acid and formate present after the neutralization reaction.

A We begin by calculating the millimoles of formic acid and formate present in 100 mL of the initial pH 3.95 buffer:

The millimoles of \(H^+\) in 5.00 mL of 1.00 M HCl is as follows:

B Next, we construct an ICE table:

\[HCO^{2−} (aq) + H^+ (aq) \rightarrow HCO_2H (aq) \]

	\(HCO^{2−} (aq) \)	\(H^+ (aq) \)	\(HCO_2H (aq) \)
Initial	21.5 mmol	5.00 mmol	13.5 mmol
Change	−5.00 mmol	−5.00 mmol	+5.00 mmol
Equilibrium	16.5 mmol	∼0 mmol	18.5 mmol

The final amount of \(H^+\) in solution is given as “∼0 mmol.” For the purposes of the stoichiometry calculation, this is essentially true, but remember that the point of the problem is to calculate the final \([H^+]\) and thus the pH. We now have all the information we need to calculate the pH. We can use either the lengthy procedure of Example \(\PageIndex{1}\) or the Henderson–Hasselbach approximation. The latter approach is much simpler. The Henderson-Hasselbalch approximation requires the concentrations of \(HCO_2^−\) and \(HCO_2H\), which can be calculated using the number of millimoles (\(n\)) of each and the total volume (\(VT\)). Substituting these values into the Henderson-Hasselbalch approximation,

\[pH=pK_a+\log \left( \dfrac{[HCO_2^−]}{[HCO_2H]} \right)=pK_a+\log\left(\dfrac{n_{HCO_2^−}/V_f}{n_{HCO_2H}/V_f}\right)=pK_a+\log \left(\dfrac{n_{HCO_2^−}}{n_{HCO_2H}}\right)\]

Because the total volume appears in both the numerator and denominator, it cancels. We therefore need to use only the ratio of the number of millimoles of the conjugate base to the number of millimoles of the weak acid. So

\[pH=pK_a+\log\left(\dfrac{n_{HCO_2^−}}{n_{HCO_2H}}\right)=3.75+\log\left(\dfrac{16.5\; mmol}{18.5\; mmol}\right)=3.75 −0.050=3.70\]

Once again, this result makes sense on two levels. First, the addition of \(HCl \)has decreased the pH from 3.95, as expected. Second, the ratio of \(HCO_2^−\) to \(HCO_2H\) is slightly less than 1, so the pH should be between the \(pK_a\) and \(pK_a\) − 1.

A The procedure for solving this part of the problem is exactly the same as that used in part (a). We have already calculated the numbers of millimoles of formic acid and formate in 100 mL of the initial pH 3.95 buffer: 13.5 mmol of \(HCO_2H\) and 21.5 mmol of \(HCO_2^−\). The number of millimoles of \(OH^-\) in 5.00 mL of 1.00 M \(NaOH\) is as follows:

B With this information, we can construct an ICE table.

\[HCO_2H (aq) + OH^− (aq) \rightarrow HCO^−_2 (aq) + H_2O (l) \]

	\(HCO_2H (aq) \)	\(OH^−\)	\(HCO^−_2 (aq) \)
Initial	13.5 mmol	5.00 mmol	21.5 mmol
Change	−5.00 mmol	−5.00 mmol	+5.00 mmol
Equilibrium	8.5 mmol	∼0 mmol	26.5 mmol

The final amount of \(OH^-\) in solution is not actually zero; this is only approximately true based on the stoichiometric calculation. We can calculate the final pH by inserting the numbers of millimoles of both \(HCO_2^−\) and \(HCO_2H\) into the simplified Henderson-Hasselbalch expression used in part (a) because the volume cancels:

\[pH=pK_a+\log \left(\dfrac{n_{HCO_2^−}}{n_{HCO_2H}}\right)=3.75+\log \left(\dfrac{26.5\; mmol}{8.5\; mmol} \right)=3.75+0.494=4.24\]

Once again, this result makes chemical sense: the pH has increased, as would be expected after adding a strong base, and the final pH is between the \(pK_a\) and \(pK_a\) + 1, as expected for a solution with a \(HCO_2^−/HCO_2H\) ratio between 1 and 10.

Exercise \(\PageIndex{3}\)

The buffer solution from Example \(\PageIndex{2}\) contained 0.119 M pyridine and 0.234 M pyridine hydrochloride and had a pH of 4.94.

What is the final pH if 12.0 mL of 1.5 M \(NaOH\) are added to 250 mL of this solution?
What is the final pH if 12.0 mL of 1.5 M \(HCl\) are added?

Answer a: 5.30
Answer b: 4.42

Note

Either concentrations OR amounts (in moles or millimoles) of the acidic and basic components of a buffer may be used in the Henderson-Hasselbalch approximation, because the volume cancels out in the ratio of [base]/[acid].

The results obtained in Example \(\PageIndex{3}\) and its corresponding exercise demonstrate how little the pH of a well-chosen buffer solution changes despite the addition of a significant quantity of strong acid or strong base. Suppose we had added the same amount of \(HCl\) or \(NaOH\) solution to 100 mL of an unbuffered solution at pH 3.95 (corresponding to \(1.1 \times 10^{−4}\) M HCl). In this case, adding 5.00 mL of 1.00 M \(HCl\) would lower the final pH to 1.32 instead of 3.70, whereas adding 5.00 mL of 1.00 M \(NaOH\) would raise the final pH to 12.68 rather than 4.24. (Try verifying these values by doing the calculations yourself.) Thus the presence of a buffer significantly increases the ability of a solution to maintain an almost constant pH.

Medicine: The Buffer System in Blood

The normal pH of human blood is about 7.4. The carbonate buffer system in the blood uses the following equilibrium reaction:

\[\ce{CO2}(g)+\ce{2H2O}(l)⇌\ce{H2CO3}(aq)⇌\ce{HCO3-}(aq)+\ce{H3O+}(aq)\]

The concentration of carbonic acid, H₂CO₃ is approximately 0.0012 M, and the concentration of the hydrogen carbonate ion, \(\ce{HCO3-}\), is around 0.024 M. Using the Henderson-Hasselbalch equation and the pK_a of carbonic acid at body temperature, we can calculate the pH of blood:

\[\mathrm{pH=p\mathit{K}_a+\log\dfrac{[base]}{[acid]}=6.1+\log\dfrac{0.024}{0.0012}=7.4}\]

The fact that the H₂CO₃ concentration is significantly lower than that of the \(\ce{HCO3-}\) ion may seem unusual, but this imbalance is due to the fact that most of the by-products of our metabolism that enter our bloodstream are acidic. Therefore, there must be a larger proportion of base than acid, so that the capacity of the buffer will not be exceeded.

Lactic acid is produced in our muscles when we exercise. As the lactic acid enters the bloodstream, it is neutralized by the \(\ce{HCO3-}\) ion, producing H₂CO₃. An enzyme then accelerates the breakdown of the excess carbonic acid to carbon dioxide and water, which can be eliminated by breathing. In fact, in addition to the regulating effects of the carbonate buffering system on the pH of blood, the body uses breathing to regulate blood pH. If the pH of the blood decreases too far, an increase in breathing removes CO₂ from the blood through the lungs driving the equilibrium reaction such that [H₃O⁺] is lowered. If the blood is too alkaline, a lower breath rate increases CO₂ concentration in the blood, driving the equilibrium reaction the other way, increasing [H⁺] and restoring an appropriate pH.

Summary

A solution containing a mixture of an acid and its conjugate base, or of a base and its conjugate acid, is called a buffer solution. Unlike in the case of an acid, base, or salt solution, the hydronium ion concentration of a buffer solution does not change greatly when a small amount of acid or base is added to the buffer solution. The base (or acid) in the buffer reacts with the added acid (or base).

Key Equations

pK_a = −log K_a
pK_b = −log K_b
\(\mathrm{pH=p\mathit{K}_a+\log\dfrac{[A^- ]}{[HA]}}\)

Glossary

buffer: mixture of a weak acid or a weak base and the salt of its conjugate; the pH of a buffer resists change when small amounts of acid or base are added

Henderson-Hasselbalch equation: equation used to calculate the pH of buffer solutions

Contributors

Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).