11.1: Introduction to Crystal Field Theory (Octahdral complexes)
- Page ID
- 280531
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)One of the most striking characteristics of transition-metal complexes is the wide range of colors they exhibit. In this section, we describe crystal field theory (CFT), a bonding model that describes the electronic structure of transition metal complexes, with an explicit focus on the five valence d-orbitals. This model can be used to explain many important properties of transition-metal complexes, including their colors and magnetism. The central (naive) assumption of CFT is that metal-ligand interactions are purely electrostatic, and that the electrons in metal d-orbitals are repelled by the ligands' electrons. Even though this assumption is clearly not valid, this theory enables chemists to explain many of the properties of transition-metal complexes with a reasonable degree of accuracy. The Learning Objective of this Module is to understand how crystal field theory explains the electronic structures and colors of metal complexes.
d-Orbital Splittings
CFT focuses on the interaction of the five valence (\((n-1)d\)) orbitals with a "field" of negative charge (electrons) from ligands arranged around a transition-metal ion. We will focus on the application of CFT to octahedral complexes, which are by far the most common and the easiest to visualize. Other common structures, such as square planar complexes, can be treated as a distortion of the octahedral model.
CFT, was developed to explain the interesting spectroscopic properties (eg various colors) of transition metal complexes. It was developed, quite literally, on the back of a napkin as two faculty members discussed how they might explain the observations of their UV-vis spectra. It was never meant to describe bonding. In fact, at the time of its development, bonding in metals was not considered covalent. Only later, with development of Ligand Field Theory and Molecular Orbital Theory, was the nature of bonding in transition metals described.
We begin by considering how the energies of the d orbitals of a transition-metal ion are affected by an octahedral arrangement of six negative charges. Recall that the five d orbitals are initially degenerate (have the same energy). If we add ligands and distribute their electrons' negative charges uniformly over the surface of a sphere, the d orbitals remain degenerate, but their energy will be higher due to repulsive electrostatic interactions between the spherical shell of negative charge and electrons in the d orbitals (part (a) in Figure \(\PageIndex{1}\)). Placing the six negative charges at the vertices of an octahedron does not change the average energy of the d orbitals, but it does remove their degeneracy: the five d orbitals split into two groups whose energies depend on their orientations. As shown in part (b) in Figure \(\PageIndex{1}\), the
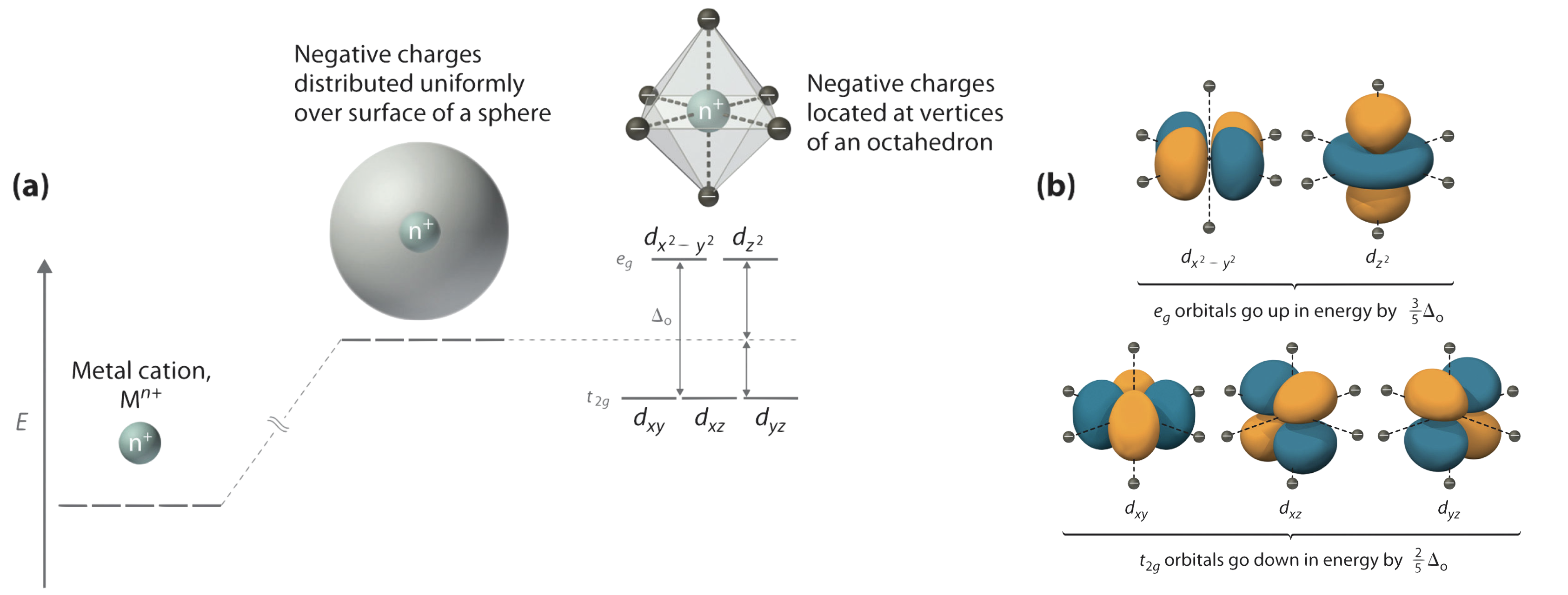
The difference in energy between the two sets of d orbitals is called the crystal field splitting energy (\(\Delta_o\), where the subscript o stands for octahedral. As we shall see, the magnitude of the splitting depends on the charge on the metal ion, the position of the metal in the periodic table, and the nature of the ligands. (Crystal field splitting energy also applies to other geometries. For example, in tetrahedral complexes a t subscript indicates tetrahedral: \(\Delta_t\).) It is important to note that the splitting of the d orbitals in a crystal field does not change the total energy of the five d orbitals: the two \(e_g\) orbitals are increased in energy by \(0.6\Delta_o\), and thus contribute a total energy of \(2 \times 0.6\Delta_o=1.2\Delta_o\). The three \(t_{2g}\) orbitals decrease in energy by \(-0.4\Delta_o\), and thus contribute a total energy of \(3 \times -0.4\Delta_o=-1.2\Delta_o\). The total change in energy is \(2(0.6\Delta_o) + 3(-0.4\Delta_o) = 0\).
Crystal field splitting does not change the total energy of the d orbitals.
But, the crystal field slplitting can change the energy of the electrons. For example, in a \(d^1\) metal in an octahedral field, the lone electron would occupy one of the lower-energy orbitals. This electrn would be stabilized (due to a decrease in energy) by \(1\text{electron} \times -0.4\Delta_o = -0.4\Delta_o\). The energy difference between the the hypothetical electron configuration of the degenerate orbitals, and that of the electrons in the ligand field is called the Crystal Field Stabilization Energy (CFSE). This is very similar to the concepts of Ligand Field Stabilization Energy (LFSE), which will be discussed later in this unit.
Electronic Structures of Octahedral Metal Complexes
We can use the d-orbital energy-level diagram in Figure \(\PageIndex{1}\): to predict electronic structures and some of the properties of transition-metal complexes. We start with the Ti3+ ion, which contains a single d electron, and proceed across the first row of the transition metals by adding a single electron at a time. We place additional electrons in the lowest-energy orbital available, while keeping their spins parallel as required by Hund’s rule. As shown in Figure \(\PageIndex{2}\), for d1–d3 systems—such as [Ti(H2O)6]3+, [V(H2O)6]3+, and [Cr(H2O)6]3+, respectively—the electrons successively occupy the three degenerate \(t_{2g}\) orbitals with their spins parallel, giving one, two, and three unpaired electrons, respectively. We can summarize this for the complex [Cr(H2O)6]3+, for example, by saying that the chromium ion has a d3 electron configuration or, more succinctly, Cr3+ is a d3 ion.
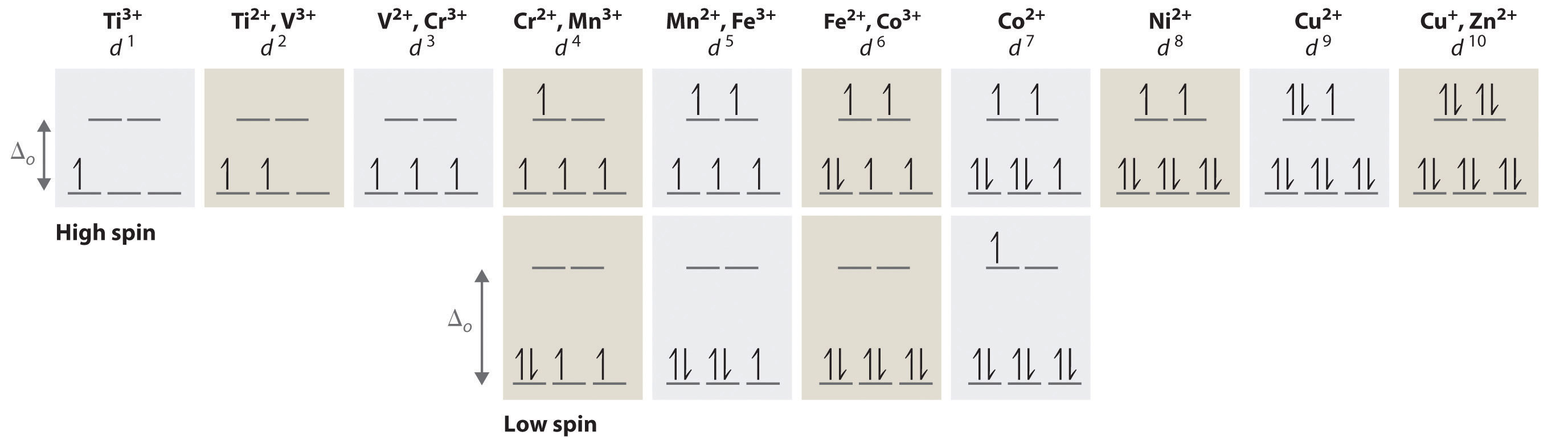
Figure \(\PageIndex{2}\): The Possible Electron Configurations for Octahedral dn Transition-Metal Complexes (n = 1–10). Two different configurations are possible for octahedral complexes of metals with d4, d5, d6, and d7 configurations; the magnitude of \(\Delta_o\) determines which configuration is observed.
When we reach the d4 configuration, there are two possible choices for the fourth electron: it can occupy one of the empty \(e_{g}\) orbitals, or it can pair in one of the singly occupied \(t_{2g}\) orbitals. The \(e_g\) orbitals are at a higher energy level, and so there is an energy cost associated with an electron occupying an \(e_g\) rather than a lower-energy \(t_{2g}\); that energy cost is equal to \(\Delta_o\). But there is another cost associated with pairing electrons in the lower-energy \(t_{2g}\) orbitals. Pairing two electrons in the same orbital causes electron-electron repulsion; this energy cost is called the spin-pairing energy (P). The more favorable electron configuration will be the one that minimizes the lenergy of the entire system. If (\Delta_o\) is less than P, then the lowest-energy arrangement has the fourth electron \(e_{g}\) orbitals. Conversely, if (\Delta_o\) is greater than P, then the lowest-energy arrangement has the fourth electron in one of the occupied \(t_{2g}\) orbitals.
When there are two possible electron configurations (eg the cases of \(d^4-d^7\)), the arrangement that results in more unpaired electrons is called a high-spin configuration. A complex that has a high-spin configuration (eg [Cr(H2O)6]2+ ion) is called a high-spin complex. The arrangement that results in less unpaired electrons is called a low-spin configuration, and a complex with this electron configuration (eg [Mn(CN)6]3− ion) is called a low-spin complex. Similarly, metal ions with the \(d^4, \; d^5, \; d^6, \), or \(d^7\) electron configurations have either high spin or low spin electron configurations, depending on the magnitude of \(\Delta_o\). Complexes that have large \(\Delta_o\) are also called "strong field" while those that have small \(\Delta_o\) are also called "weak field".
In contrast, only one arrangement of d electrons is possible for metal ions with d8–d10 electron configurations. For example, the [Ni(H2O)6]2+ ion is d8 with two unpaired electrons, the [Cu(H2O)6]2+ ion is d9 with one unpaired electron, and the [Zn(H2O)6]2+ ion is d10 with no unpaired electrons. It is incorrect to refer to these complexes or their electron configurations as high-spin or low-spin. However, we can refer to them in terms of the magnitude of \(\Delta_o\) and the relative "strength" on the ligand field.
If Δo is less than the spin-pairing energy, a high-spin configuration results. Conversely, if \(\Delta_o\) is greater, a low-spin configuration forms.


