11.2: Introduction to Ligand Field Theory (Octahedral complexes)
- Page ID
- 280532
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Concepts from molecular orbital (MO) theory are useful in understanding the reactivity of coordination compounds. One of the basic ways of applying MO concepts to coordination chemistry is in Ligand Field Theory (LFT). LFT is essentially a version of MO theory that focuses on how the d-orbitals of a metal ion interact with ligand orbitals to create bonding, antibonding, and non-bonding interactions. These interactions result in orbitals that are close in energy to the original d-orbitals of the metal. Due to their similarity to the metal d-orbitals, they are usually referred to as the metal d-orbitals even though they are actually molecular orbitals. The interactions of ligand orbitals with metal d-orbitals results in different splitting of the metal d-orbitals into sets of bonding, antibonding and non-bonding orbitals. In the octahedral case, the splitting of d-orbitals is the same in LFT as we saw previously in CFT. The main difference between the two theories is the explanation of how this splitting is derived. LFT also describes bonding, while CFT can't.
The symmetry of the central metal orbital and that of the ligand group orbitals (aka SALCs, symmetry adapted linear combinations of atomic orbitals) determines the relative eenergies (eg the splitting) of the d-oritals of the metal complex. The symmetry of the SALCs depends on the coordination geometry of the ligands and the specific type of orbitals involved (eg \(s\) vs \(p\)). For example, ligand \(s\) orbitals in a tetrahedral coordination sphere will have a different symmetries and different abilities to interact with the metal d-orbitals than orbitals in an octahedral coordination sphere because they will interact with the different d orbitals in different ways.
Ligand Field Theory looks at the effect of donor atoms on the energy of d orbitals in the metal complex.
The effect depends on the coordination geometry of the ligands.
A simple octahedral case
Let's start with an example of six ligand s-orbitals in an octahedral coordination structure. Assume the six ligands all lie along the x, y and z axes and that they interact with the metal using just their \(s\) orbitals (see Figure \(\PageIndex{1}\)).
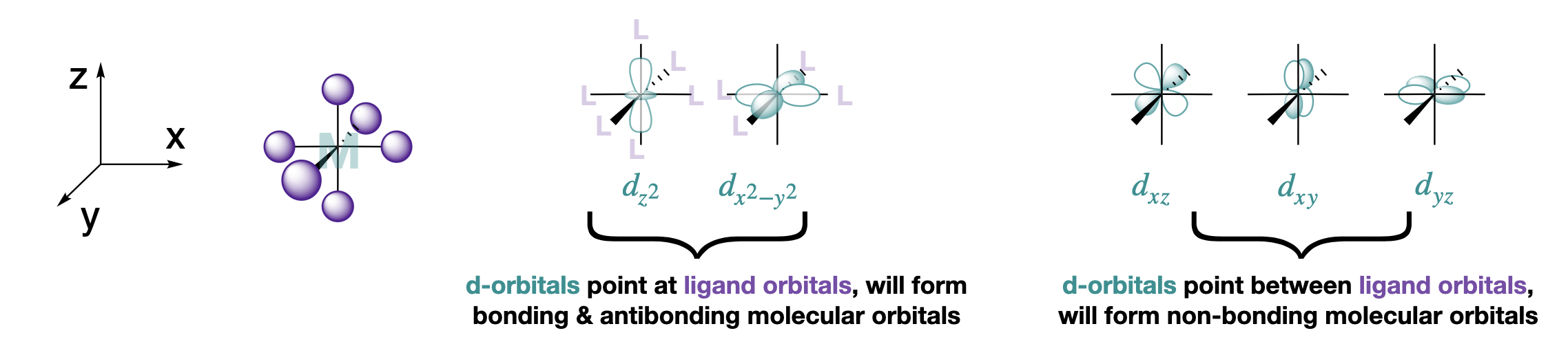
Because the ligand \(s\) orbitals lie on the axes, there are two \(d\) orbitals that will form productive interactions with these ligands: the \(d_{x^2-y^2}\) which has lobes that point directly along the x and y axes, and the \(d_{z^2}\), which has lobes that point along the z axis and along the \(xy\) plane. The ligand s orbitals have two SALCs with appropriate symmetry to interact with these two metal d-orbitals. However, the remaining three orbitals, the \(d_{xy}, \; d_{xz},\) and \(d_{yz}\), cannot form productive interactions with ligand s-orbitals.
Exercise \(\PageIndex{1}\)
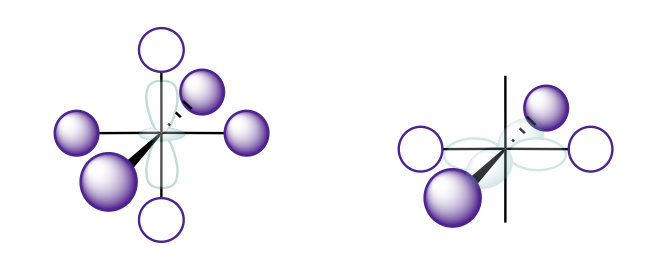
Sketch the two ligand SALCs that would interact with the d-orbitals, as shown in Figure \(\PageIndex{1}\). What is the symmetry of these SALCs under the octahedral point group?
- Answer
-
The sketches are shown below, where the purple lobes show the group orbital and the teal transparent orbital in the center is the d-orbital with compatible symmetry. These sketches were drawn simply by matching the symmetry of the central metal orbital. A full explanation for how to systematically generate such sketches is described in a previous chapter. The octahedral character table tells us that the (d_{x^2-y^2}\) and \(d_{z^2}\) orbitals transform together with \(e_g\) symmetry. Thus, the two SALCs sketched below would also transform with \(e_g\) symmetry.
The metal \(d_{x^2-y^2}\) and \(d_{z^2}\) will combine with the \(e_g\) SALCs (see exercise above) to form new bonding and antibonding molecular orbitals. A simplified drawing of this interaction, which forms bonding and antibonding molecular orbitals is shown below in Figure \(\PageIndex{2}\). There are also for other ligand SALCs that will interact with s and p orbitals, but for the moment we're not going to worry about them.
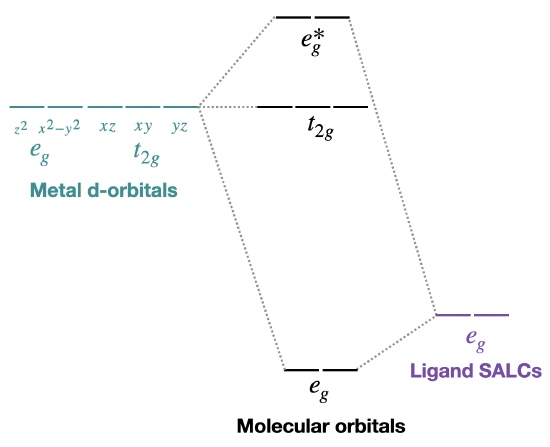
Figure \(\PageIndex{2}\): Diagram of metal d orbitals (left) and ligand \(e_g\) SALCs (right) along with their relative energies. The orbitals in the middle represent the molecular orbitals: there is a set of bonding \(e_g\), a set of antibonding \(e_g^*\), and set of non-bonding \(t_{2g}\) orbitals. The metal d-orbitals are considered to be "split" into the \(t_{2g}\) and \(e_g^*\) molecular orbitals, while the bonding \(e_g\) have mostly ligand character (this is all based on relative energies of molecular orbitals compared to metal and ligand atomic orbtials. Energy increases from bottom to top. (CC-BY-NC-SA; Kathryn Haas)
Now, remember that metals usually have d electrons that are much higher in energy than those on typical donor atoms (like oxygen, sulfur, nitrogen or phosphorus). That means the antibonding combinations will be much closer in energy to the original d orbitals, because both are relatively high in energy. The bonding combination will be much closer in energy to the original ligand orbitals, because these ones are all relatively low in energy.
That energetic similarity generally translates into a similarity in shape and location as well. In other words, the antibonding combination between a d orbital and a ligand orbital is a lot like the original d orbital. The bonding combination is more like the original ligand orbital than the original d orbital. Because of those similarities, inorganic chemists often refer to those antibonding orbitals as if they were still the original d orbitals.
Exercise \(\PageIndex{1}\)
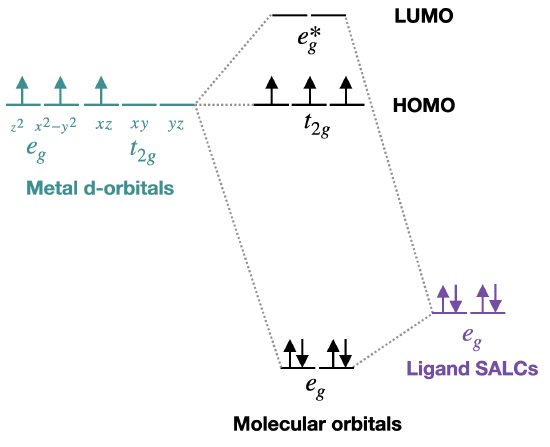
Use the diagram in Figure \(\PageIndex{2}\). Fill in the diagram for a \(d^3\) metal complex. Identify the froteir orbtials (the HOMO and the LUMO).
- Answer
-
When filling in electrons to this diagram we assume that each ligand bonds to the metal by donating two electrons; two SALCs results in four ligand electrons to add to the system. The metal has three d orbitals according to the description. The molecular orbitals should then be filled starting with the lowest energy orbitals. The HOMO-LUMO gap is between the \(t_{2g}\) non-bonding and \(e_g^*\) antibonding orbitals:
Summary for simple octahedral case
- Assume the six ligands all lie along the x, y and z axes.
- The \(d_{x^2-y^2}\) and the \(d_{z^2}\) orbitals point at the ligands along the axes.
- These two orbitals "become" antibonding orbitals and are thus "raised" relatively high in energy.
- These orbitals are called the "eg" set of orbitals due to their symmetry under the octahedral point group.
On the other hand, the other three d orbitals, the dxy, dxz and dyz, all lie between the donor ligands, rather than hitting them head-on. These orbitals will interact less strongly with the donor electrons.
- The dxy, dxz and dyz orbitals all lie between the bond axes.
- These three orbitals will be changed in energy only a little.
- These orbitals are more like non-bonding orbitals.
- These orbitals are sometimes called the "t2g" set of orbitals.
Remember, only the energy of the electrons affects the overall energy of the system. The unoccupied d orbitals are raised in energy, but the occupied orbitals go down in energy (or else stay the same).
Apart from the stabilization of the complex, there is another consequence of this picture. What we are left with is two distinct sets of d energy levels, one lower than the other. That will have an effect on the electron configuration at the metal atom in the complex. In other words, there will be cases where electrons could be paired or unpaired, depending on how these orbitals are occupied.
Take the case of the biologically important iron(II) ion. It has a d6 valence electron configuration. In less formal parlance of inorganic chemistry, "iron(II) is d6." In an iron(II) ion all alone in space, all the d orbitals would have the same energy level. We would put one electron in each orbital, and have one left. The left over electron would need to pair up in one of the d orbitals (Notice that, in the chemistry of transition metal ions, the valence s and p orbitals are always assumed to be unoccupied).
Things are very different in an octahedral complex, like K4[Fe(CN)6]. In that case, the d orbitals are no longer at the same energy level. There are two possible configurations to consider.
In one case, one electron would go into each of the lower energy d orbitals. A choice would be made for the fourth electron. Does it go into the higher energy d orbital, or does it pair up with one of the lower energy d electrons? The choice depends on how much higher in energy the upper d orbitals are, compared to how much energy it costs to put two electrons in the same d orbital.
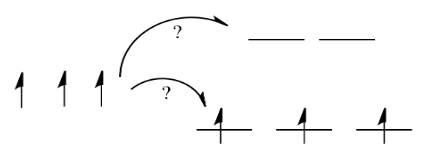
If the "d orbital splitting energy" is pretty low, so that the two sets of d orbitals are still pretty similar in energy, the next electron can go into a higher orbital. Pairing would not be required until the final electron. Overall, that would leave four unpaired electrons, just like in the case of a lone metal ion in space. This is called the "high-spin" case, because electrons can easily go into the higher orbital.
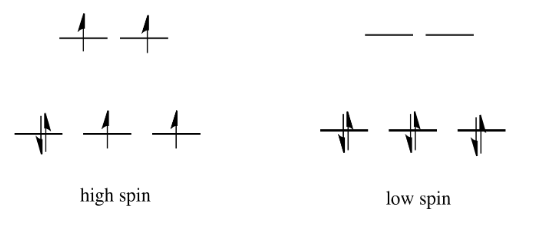
If the d orbital splitting energy is too high, the next electron must pair up in a lower orbital. All three remaining electrons pair up, and so there are no unpaired electrons in the complex. This is called the "low-spin" case, because electrons more easily pair up in the orbital.
So the overall rule is that if the energy to pair up the electrons is greater than the energy needed to get to the next level, the electron will go ahead and occupy the next level.
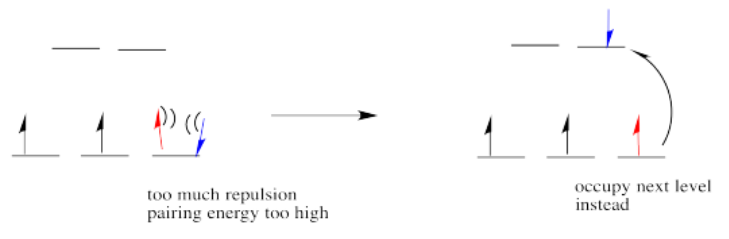
However, if the energy it takes to get to the next level is more than it would cost to pair up, the electrons will just pair up instead.
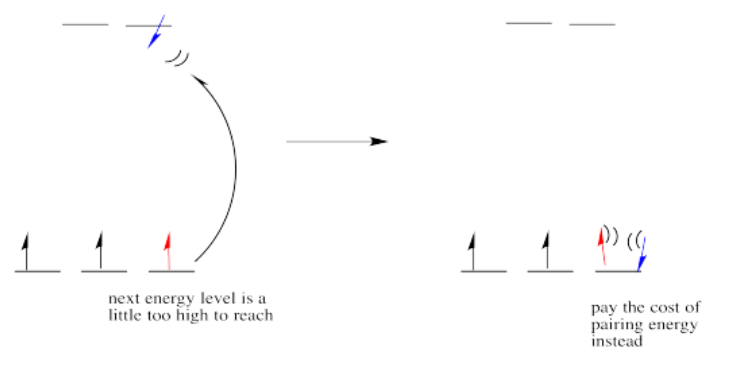
The electron configuration can be "high spin" or "low-spin", depending on how large the energy splitting is between the two sets of d orbitals.
The difference between the high-spin case and the low-spin case is significant because unpaired electrons affect the magnetic properties of a material. The low-spin case would be diamagnetic, resulting in no interaction with a magnetic field. However, the high-spin case would be paramagnetic, and would be attracted to a magnetic field.
It turns out K4[Fe(CN)6] is diamagnetic. Thus, it is pretty clear that it is a low-spin complex. The energy difference between the two d orbital levels is relatively large in this case.
In addition to influencing magnetic properties, whether a complex is high- or low-spin also influences reactivity. Compounds with high-energy d electrons are generally more labile, meaning they let go of ligands more easily.
- electron configuration influences magnetic properties
- electron configuration influences lability (how easily ligands are released)


