7.2.2: Trends in M-L lability (Kinetics)
- Page ID
- 206988
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
Kinetics is a branch of chemistry that is concerned with the rates of chemical reactions. In this section, we will discuss the rates of metal-ligand (M-L) substitution reactions.
Let's start with some examples. In the table below are three examples of ligand substitution reactions of hexaaquo metal complexes to form hexaammine complexes. These reactions are nearly identical with the exception of the metal ion. The products are thermodynamically favored in all cases.
| Reaction | Rate constant (\(k\)) | Labile or Inert |
|---|---|---|
| \([Ni(OH_2)]^{2+} + 6 NH_3 \rightleftharpoons [Ni(NH_3)_6]^{2+}\) | \(k = 10^{4} s^{-1}\) (1 ns) |
Labile (happens in < 1 min) |
| \([Cr(OH_2)]^{2+} + 6 NH_3 \rightleftharpoons [Cr(NH_3)_6]^{2+}\) |
\(k = 10^{-3} s^{-1}\) (6 days) |
Inert (slow, takes hours) |
| \([Cu(OH_2)]^{2+} + 6 NH_3 \rightleftharpoons [Cu(NH_3)_6]^{2+}\) | \(k = 10^{8} s^{-1}\) | Very Labile (happens in seconds) |
- Labile - Metal complexes that undergo "kinetically fast" substitution reactions are labile. These reactions usually happen in less than one minute.
- Inert - Metal complexes that undergo "kinetically slow" substitution reactions are inert or non-labile. These reactions usually take hours.
- Intermediate - Metal complexes that undergo "kinetically intermediate" substitution reactions are intermediate.
A common pitfall is to confuse the meaning of kinetic terms, like labile and inert, with thermodynamic terms, like stable and unstable. It is important to distinguish between kinetics and thermodynamics. For example, the complex \([Fe(H_2O)Cl]^{2+}\) has a large formation constant and is thermodynamically stable; yet it is also labile. On the other hand, the complex \([Co(NH_3)_6]^{3+}\) is unstable in acidic aqueous solution and decomposes spontaneously to \([Co(H_2O)_6]^{3+}\); yet it decomposes slowly because it is inert. It is good practice to distinguish between meanings by using terms such as "kinetically labile" or "kinetically inert" and "thermodynamically stable" and "thermodynamically unstable".
Draw the reaction coordinate diagrams for a reaction of the form \([ML_6]^{n+} + X \rightleftharpoons [ML_5X]^{n+} + L\) in the following scenarios:
- \([ML_6]^{n+}\) is theromdynamically stable and kinetically inert.
- \([ML_6]^{n+}\) is theromdynamically unstable and kinetically inert.
- \([ML_6]^{n+}\) is theromdynamically stable and kinetically labile.
- \([ML_6]^{n+}\) is theromdynamically unstable and kinetically labile.
- Answer a)
-
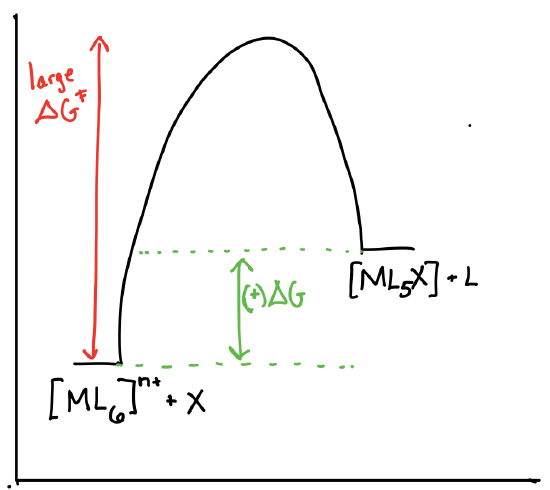
- Answer b)
-

- Answer c)
-
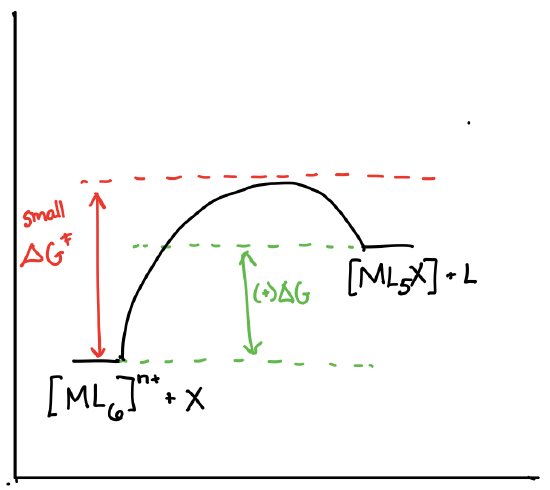
- Answer d)
-

Factors that affect rates of substitution reactions:
Some of the factors that affect rates of ligand substitution reactions are those that also affect thermodynamic stability. It is important to remember that kinetic and thermodynamic factors are related, yet separate. The same factors that make a complex stable can also make it more inert. However, it is incorrect to assume that stability is always correlated with reaction rates.
Why are kinetic factors related to thermodynamic stability? For a complex to react or exchange one ligand for another, it must change its geometry to form an intermediate or transition state. For example, inert octahedral complexes often have stable electron configurations. When the reactant electron configuration is particularly stable, it can result in a higher activation energy associated with moving away from the stable configuration.
Factors to consider:
- Electron configuration and LFSE: Electron configurations that place electrons in higher-energy orbitals (particularly antibonding orbitals) result in more labile complexes. As long as there are not electrons in higher-energy orbitals, the lability correlates roughly with LFSE. The more negative the LFSE, the more inert.
- Size and charge of the metal ion: In general, higher charge denisity on the metal ion leads to stronger electrostatic attraction between metal and ligand; higher charge density generally correlates with slower rates of ligand substitution.
Consider all possible electron configurations for octahedral complexes (\(d^0\) to \(d^{10}\), high spin and low spin cases): predict whether each case would be inert, intermediate, or labile.
- Answer
-

Put the metal ions in order of decreasing reaction rate (from labile to inert):
a) \(Al^{3+}, Na^+, Mg^{2+}\)
b) \(Ca^{2+}, Mg^{2+}, Sr^{2+} \)
- Answer (a)
-
Most Labile to most inert: \(Na^+ > Mg^{2+} > Al^{3+}\)
These are metal ions with similar size and varying charge. They are in order of increasing charge and increasing density from left to right.
- Answer (b)
-
Most labile to most inert: \(Sr^{2+} > Ca^{2+} > Mg^{2+}\)
These metal ions have the same charge, and vary in size. They are in order of decreasing charge and increasing charge density from left to right.
Overall Generalizations for Kinetics:
- s-block metals are very labile, except for those with very high charge density (eg. \(Mg^{2+}\ is\: inert\))
- \(d^{10}\) metals are labile (eg: \(Zn^{2+}, Cu^+, Hg^{2+}\))
- Other ions with a full shell are labile (eg: \(Ln^{3+}\) of f-block)
- 3d \(M^{2+}\), when high spin, are generally labile (eg. \(Cu^{2+} is\: very\: labile\))
- 4d and 5d are usually inert due to higher LFSE (low spin, high LFSE)
- \(M^{2+}\) is more labile than the same metal as \(M^{3+}\)
- \(d^3\) and low spin \(d^6\) are inert (eg. \(Cr^{3+}, Co^{3+}, \) low spin \(Fe^{2+}\))
Attribution
Curated or created by Kathryn Haas

