3.3.6: Symmetry and Mixing
- Page ID
- 202272
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
Orbital Symmetry
Orbital interactions are governed by symmetry. Without taking an entire course in Group Theory (the branch of mathematics that deals with symmetry), we can learn a little bit about symmetry as we need it.
Symmetry with respect to a bond
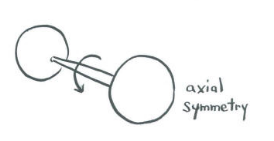
One of the most basic aspects of molecular symmetry applies to diatomic molecules. That element is symmetric about the bond axis. If a molecule is spun around its bond axis -- as if the two atoms are the two wheels on an axle of a wagon or a car -- does the orbital change its orientation?
Two s-orbitals along a bond:Two s-orbitals along a bond are completely symmetric.
|
|
|
|
|
Two p-orbitals along a bond:The symmetry of two p-orbitals along a bond depends on their direction in space. |
|
| p-orbitals that are parallel to the bond axis: Suppose the bond axis is the z-axis. Rotation about the z axis produces no change in orientation of a pz orbital. The orbital spins but does not move through space. Rotation about the z-axis does produce a visible change in orientation of a px orbital, and so it is said to by symmetric with respect to the bond. 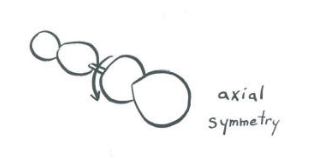 |
p-orbitals that are perpendicular to the bond axis: |
This "wagon-wheel" symmetry with respect to a bond axis is only one element of symmetry that affects bonding. For now, there is only one more type of symmetry that we should discuss: symmetry with respect to a fixed set of molecular coordinates.
Compatible symmetry
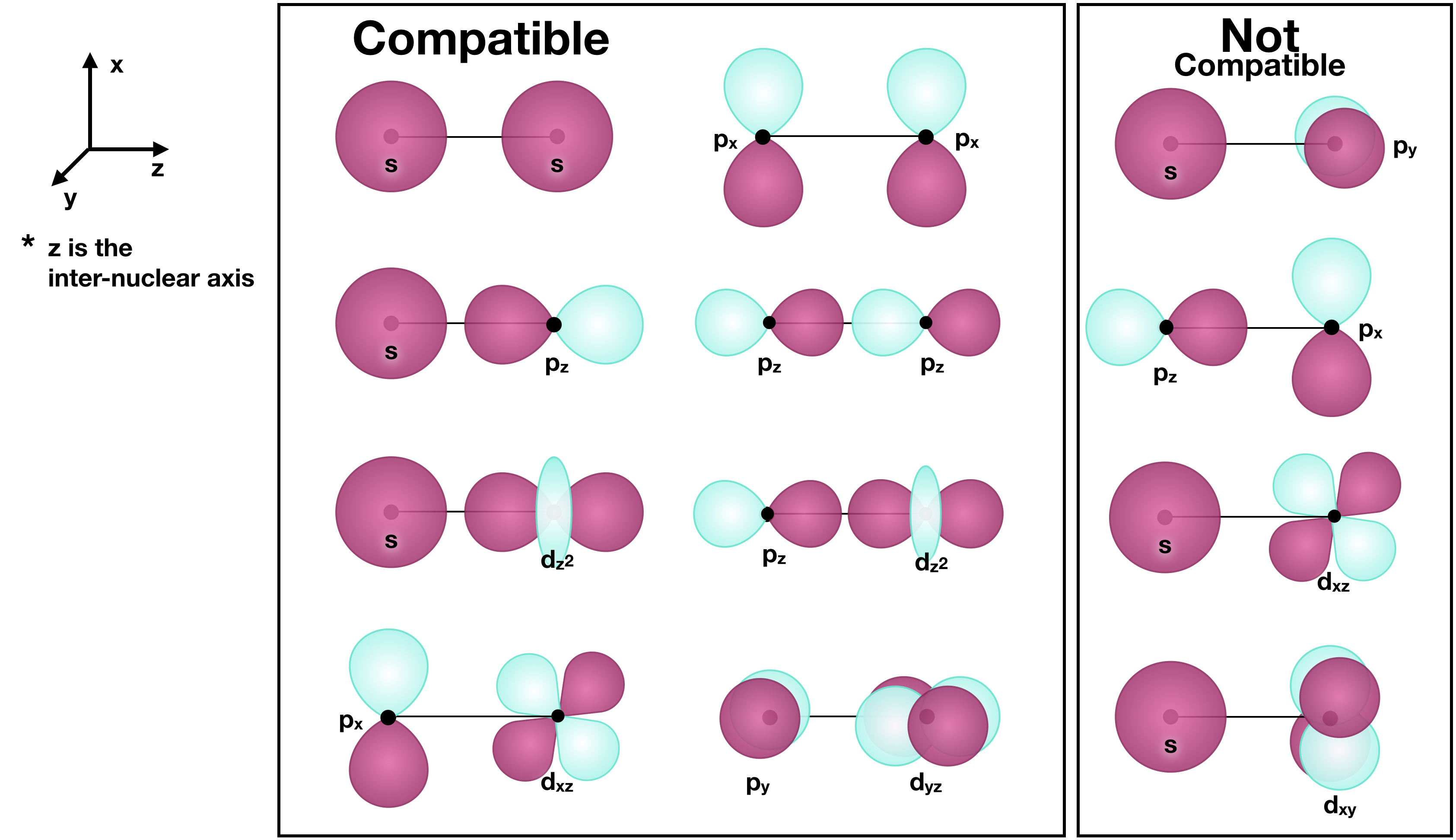
Atomic orbitals (AO's) must have compatible symmetry to combine into any type of molecular orbitals (MO's). Without getting into group theory, we can recognize compatible symmetry if we compare the shapes of atomic orbitals, along their bond axis. If there is the possibility of a net constructive or net destructive interference, then the orbitals have compatible symmetry and the ability to form MO's.
The figure below shows examples of AO’s on two atoms of a diatomic molecule that have compatible symmetry, and those that do not. The line between each set of orbitals represents the bond axis between the two atoms, and the black dot represents each nucleus.
Mixing
Our picture of main group diatomic molecules changes slightly with this news. The p bonding orbitals remain unchanged. However, the s bonding orbitals share axial symmetry. That means that the s bonding orbitals, far from keeping completely separate from each other, actually mix together in some cases. That means there can be an orbital that is composed of an s and pz orbital from one atom as well as an s and pz orbital from the other. The only restriction is that, because four atomic orbitals are allowed to mix, four new molecular orbitals must be produced.
- As a result, in diatomics, an s orbital shares an element of symmetry with one p orbital, but not with the others.
- The rules of mathematics and quantum mechanics allow s orbitals in diatomics to interact with one p orbital with which it shares symmetry, but not with the other two.
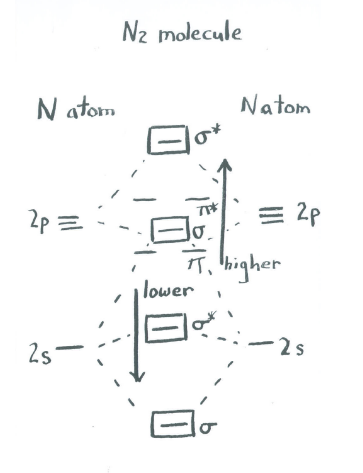
Another way of thinking about this mixing effect is to take the molecular orbital picture we already made for dinitrogen and then say that the sigma bonding orbitals can interact with each other. That means they can push each other up or down in energy, mixing together to create new combinations with new energies. The extent of this mixing varies across the periodic table.
For main group diatomics like N2, the effect is to lower the energy of the lower sigma orbitals (related to the atomic s levels) and raise the energy of the higher sigma orbitals (related to the atomic p levels). The result is that the second-highest sigma orbital is shifted slightly above the energy of the pi levels, rather than being slightly below them. This does not change the overall conclusions very much, but it is a favorable interaction because the lower-lying sigma levels, which are occupied by electrons, move to lower energy.
Attribution
Chris P Schaller, Ph.D., (College of Saint Benedict / Saint John's University)
Curated or created by Kathryn Haas