D. Consequences of d-orbital Spitting
- Page ID
- 59600
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The energy level splitting of the d-orbitals due to their interaction with the ligands in a complex has important structural and thermodynamic effects on the chemistry of transition-metal complexes. Although these two types of effects are interrelated, they are considered separately here.
Structural Effects
There are two major kinds of structural effects: effects on the ionic radii of metal ions with regular octahedral or tetrahedral geometries, and structural distortions observed for specific electron configurations.
Ionic Radii
Figure \(\PageIndex{1}\) is a plot of the ionic radii of the divalent fourth-period metal ions versus atomic number. The dashed line represents the behavior predicted based on the effects of screening and variation in effective nuclear charge (Zeff), assuming a spherical distribution of the 3d electrons. Because these radii are based on the structures of octahedral complexes and Cr2+ and Cu2+ do not form truly octahedral complexes, the points for these ions are shown as open circles.
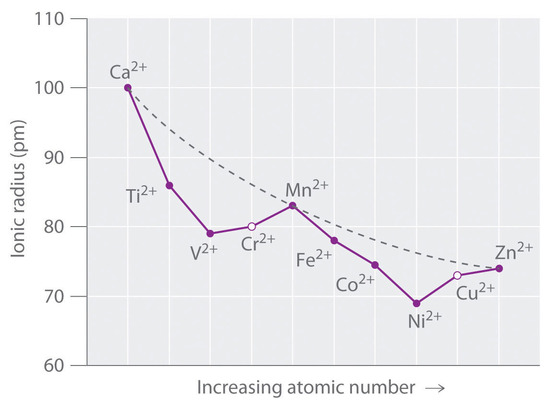
A similar effect is observed for the V2+ ion, which has a d3 configuration. Because the three electrons in the t2g orbitals provide essentially no shielding of the ligands from the metal, the ligands experience the full increase of +1 in nuclear charge that occurs from Ti2+ to V2+. Consequently, the observed ionic radius of the V2+ ion is significantly smaller than that of the Ti2+ ion.
Skipping the Cr2+ ion for the moment, consider the d5 Mn2+ ion. Because the nuclear charge increases by +2 from V2+ to Mn2+, Mn2+ might be expected to be smaller than V2+. The two electrons added from V2+ to Mn2+ occupy the eg orbitals, however, which are oriented directly toward the six ligands. Because these electrons are localized directly between the metal ion and the ligands, they are effective at screening the ligands from the increased nuclear charge. As a result, the ionic radius actually increases significantly from V2+ to Mn2+, despite the higher nuclear charge of the latter.
The same effects are observed in the second half of the first-row transition metals. In the Fe2+, Co2+, and Ni2+ ions, the extra electrons are added successively to the t2g orbitals, resulting in increasingly poor shielding of the ligands from the nuclei and in abnormally small ionic radii. Skipping over Cu2+, adding the last two electrons causes a significant increase in the ionic radius of Zn2+, despite its greater nuclear charge.
The Jahn–Teller Effect
Because simple octahedral complexes are not observed for the Cr2+ and Cu2+ ions, only estimated values for their radii are shown in Figure \(\PageIndex{1}\). Since both Cr2+ and Cu2+ ions have electron configurations with an odd number of electrons in the eg orbitals. Because the single electron (in the case of Cr2+) or the third electron (in the case of Cu2+) can occupy either one of two degenerate eg orbitals, both systems have degenerate ground states. The Jahn–Teller theorem states that such non-linear systems are not stable; they undergo a distortion that makes the complex less symmetrical and splits the degenerate states, which decreases the energy of the system. The distortion and resulting decrease in energy are collectively referred to as the Jahn–Teller effect. Neither the nature of the distortion nor its magnitude is specified, and in fact, they are difficult to predict. In principle, Jahn–Teller distortions are possible for many transition-metal ions; in practice, however, they are observed only for systems with an odd number of electrons in the eg orbitals, such as the Cr2+ and Cu2+ ions.
Consider an octahedral Cu2+ complex, [Cu(H2O)6]2+, which is elongated along the z axis. As indicated in Figure \(\PageIndex{2}\), this kind of distortion splits both the eg and t2g sets of orbitals. Because the axial ligands interact most strongly with the dz2 orbital, the splitting of the eg set (δ1) is significantly larger than the splitting of the t2g set (δ2), but both δ1 and δ2 are much, much smaller than the Δo. This splitting does not change the centerpoint of the energy within each set, so a Jahn–Teller distortion results in no net change in energy for a filled or half-filled set of orbitals. If, however, the eg set contains one electron (as in the d4 ions, Cr2+ and Mn3+) or three electrons (as in the d9 ion, Cu2+), the distortion decreases the energy of the system. For Cu2+, for example, the change in energy after distortion is 2(−δ1/2) + 1(δ1/2) = −δ1/2. For Cu2+ complexes, the observed distortion is always an elongation along the z axis by as much as 50 pm; in fact, many Cu2+ complexes are distorted to the extent that they are effectively square planar. In contrast, the distortion observed for most Cr2+ complexes is a compression along the z axis. In both cases, however, the net effect is the same: the distorted system is more stable than the undistorted system.
Jahn–Teller distortions are most important for d9 and high-spin d4 complexes; the distorted system is more stable than the undistorted one.
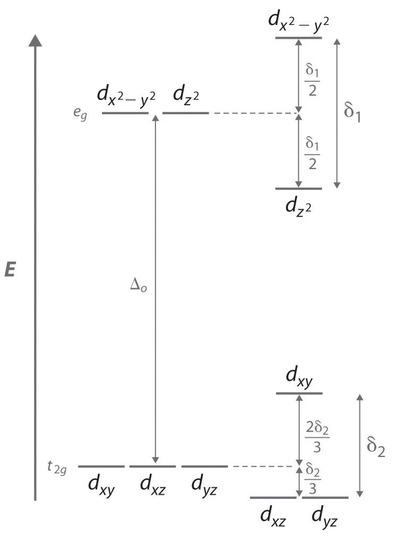
Increasing the axial metal–ligand distances in an octahedral d9 complex is an example of a Jahn–Teller distortion, which causes the degenerate pair of eg orbitals to split in energy by an amount δ1; δ1 and δ2 are much smaller than Δo. As a result, the distorted system is more stable (lower in energy) than the undistorted complex by δ1/2.
Thermodynamic Effects
As previously noted, crystal field splitting energies (CFSEs) can be as large as several hundred kilojoules per mole, which is the same magnitude as the strength of many chemical bonds or the energy change in most chemical reactions. Consequently, CFSEs are important factors in determining the magnitude of hydration energies, lattice energies, and other thermodynamic properties of the transition metals.
Hydration Energies
The hydration energy of a metal ion is defined as the change in enthalpy for the following reaction:
\[M^{2+}_{(g)} + H_2O_{(l)} \rightarrow M^{2+}_{(aq)} \label{1.1.1} \]
Although hydration energies cannot be measured directly, they can be calculated from experimentally measured quantities using thermochemical cycles. In Figure \(\PageIndex{3a}\), a plot of the hydration energies of the fourth-period metal dications versus atomic number forms a curve with two valleys. Note the relationship between the plot in Figure \(\PageIndex{3a}\) and the plot of ionic radii in Figure \(\PageIndex{1}\) the overall shapes are essentially identical, and only the three cations with spherically symmetrical distributions of d electrons (Ca2+, Mn2+, and Zn2+) lie on the dashed lines. In Figure \(\PageIndex{3a}\), the dashed line corresponds to hydration energies calculated based solely on electrostatic interactions. Subtracting the CFSE values for the [M(H2O)6]2+ ions from the experimentally determined hydration energies gives the points shown as open circles, which lie very near the calculated curve. Therefore, CFSEs are primarily responsible for the differences between the measured and calculated values of hydration energies.

Lattice Energies
Values of the lattice energies for the fourth-period metal dichlorides are plotted against atomic number in part (b) of Figure \(\PageIndex{3}\). Recall that the lattice energy is defined as the negative of the enthalpy change for the reaction below. Like hydration energies, lattice energies are determined indirectly from a thermochemical cycle.
\[M^{2+} (g) + 2Cl^− (g) \rightarrow MCl_2 (s) \label{1.1.2} \]
The shape of the lattice-energy curve is essentially the mirror image of the hydration-energy curve in part (a) of Figure \(\PageIndex{3}\), with only Ca2+, Mn2+, and Zn2+ lying on the smooth curve. It is not surprising that the explanation for the deviations from the curve is exactly the same as for the hydration energy data: all the transition-metal dichlorides, except MnCl2 and ZnCl2, are more stable than expected due to CFSE.
Summary
Distorting an octahedral complex by moving opposite ligands away from the metal produces a tetragonal or square planar arrangement, in which interactions with equatorial ligands become stronger. Because none of the d orbitals points directly at the ligands in a tetrahedral complex, these complexes have smaller values of the crystal field splitting energy Δt. The crystal field stabilization energy (CFSE) is the additional stabilization of a complex due to placing electrons in the lower-energy set of d orbitals. CFSE explains the unusual curves seen in plots of ionic radii, hydration energies, and lattice energies versus atomic number. The Jahn–Teller theorem states that a non-linear molecule with a spatially degenerate electronic ground state undergoes a geometrical distortion to remove the degeneracy and lower the overall energy of the system.

