Predicting Geometry with VSEPR
- Last updated
- Save as PDF
- Page ID
- 195503
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction to VSEPR
The Valence Shell Electron Repulsion (VSEPR) model can predict the structure of most molecules and polyatomic ions in which the central atom is a nonmetal; it also works for some structures in which the central atom is a metal. VSEPR builds on Lewis electron dot structures (discussed in Section 3.1); Lewis structures alone predict only connectivity while the Lewis structure and VSEPR together can predict the geometry of each atom in a molecule. The main idea of VSEPR theory is that pairs of electrons (in bonds and in lone pairs) repel each other. The pairs of electrons (in bonds and in lone pairs) are called "groups". Because electrons repel each other electrostatically, the most stable arrangement of electron groups (i.e., the one with the lowest energy) is the one that minimizes repulsion. Groups are positioned around the central atom in a way that produces the molecular structure with the lowest energy. In other words, the repulsion between groups around an atom favors a geometry in which the groups are as far apart from each other as possible. Although VSEPR is simplistic because it does not account for the subtleties of orbital interactions that influence molecular shapes, it accurately predicts the three-dimensional structures of a large number of compounds.
We can use the VSEPR model to predict the geometry around the atoms in a polyatomic molecule or ion by focusing on the number of electron pairs (groups) around a central atom of interest. Groups include bonded and unbonded electrons; a single bond, a double bond, a triple bond, a lone pair of electrons, or even a single unpaired electron each count as one group. The molecule or polyatomic ion is given an AXmEn designation, where A is the central atom, X is a bonded atom, E is a nonbonding valence electron group (usually a lone pair of electrons), and m and n are integers. The number of groups is equal to the sum of m and n. Using this information, we can describe the molecular geometry around a central atom, that is, the arrangement of the bonded atoms in a molecule or polyatomic ion. The geometries that are predicted from VSEPR when a central atom has only bonded groups (n = 0) are listed below in Table \(\PageIndex{1}\). The cases where lone pairs contribute to the total groups (n \(\geq\) 1) are discussed in the next section about lone pair repulsion.
|
Groups around central atom (m + n) |
Geometry Name | Geometry Sketch | Predicted bond Angle | Example |
|---|---|---|---|---|
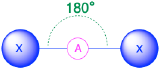
| 2 | linear | 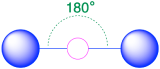 |
180° | 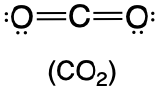 |
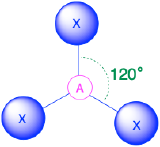
| 3 | trigonal plane | 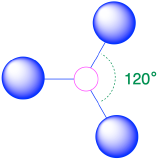 |
120° | 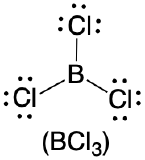 |
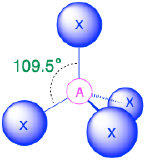
| 4 | tetrahedron | 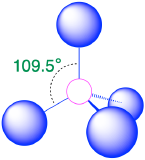 |
109.5° | 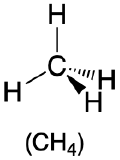 |
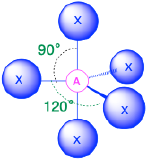
| 5 | trigonal bipyramid | 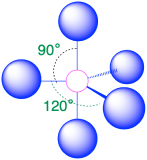 |
90° and 120° | 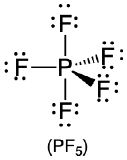 |
| 6 | octahedron | 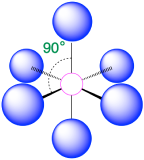 |
90° | 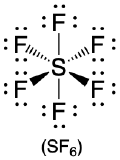 |
| 7 | pentagonal bipyramid | 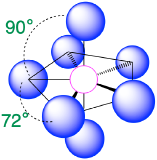 |
90° and 72° |  |
| 8 | square antiprism | 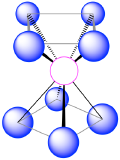 |
70.5°, 99.6° and 109.5° | 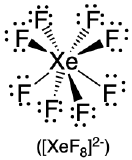 |
Practice
VSEPR to predict Molecular Geometry
You can follow these four steps to predict the geometry around an atom using VSEPR:
- Draw the Lewis electron structure of the molecule or polyatomic ion.
- For the central atom of interest, assign the AXmEn designation and the total number of groups (m+n).
- Determine the electron group arrangement around the central atom that minimizes repulsions.
- Describe the molecular geometry.
Use the procedure above to complete the exercises below
Exercise \(\PageIndex{1}\)
Predict the geometry around the central atom in BeH2 and CO2.
- Answer BeH2
-
1. The central atom, beryllium, contributes two valence electrons, and each hydrogen atom contributes one. The Lewis electron structure is

2. There are two groups around the central atom, and both groups are single bonds. Thus BeH2 is designated as AX2.
3. We see from Table \(\PageIndex{1}\) that the arrangement that minimizes repulsions places the groups 180° apart.
4. From Table \(\PageIndex{1}\) we see that with two bonding pairs, the molecular geometry that minimizes repulsions in BeH2 is linear.
- Answer CO2
-
1. The central atom, carbon, contributes four valence electrons, and each oxygen atom contributes six. The Lewis electron structure is
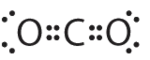
2. The carbon atom forms two double bonds. Each double bond is counted as one group, so there are two groups around the central atom. Once again, both groups around the central atom are bonds, so CO2 is designated as AX2.
3. Like BeH2, the arrangement that minimizes repulsions places the groups 180° apart.
4. VSEPR only recognizes groups around the central atom (the carbon). Thus the lone pairs on the oxygen atoms do not influence the molecular geometry. With two bonded groups on the central atom and no lone pairs, the molecular geometry of CO2 is linear (Table \(\PageIndex{1}\)). The structure of \(\ce{CO2}\) is shown in Table \(\PageIndex{1}\).
Exercise \(\PageIndex{2}\)
Predict the geometry around the central atom in BCl3 and CO32-.
- Answer BCl3
-
1. The central atom, boron, contributes three valence electrons, and each chlorine atom contributes seven valence electrons. The Lewis electron structure is
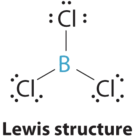
2. There are three groups around the central atom and all are single bonds. The structure is designated as AX3.
3. To minimize repulsions, the groups are placed 120° apart (Table \(\PageIndex{1}\)).
4. From Table \(\PageIndex{1}\) we see that with three bonding pairs around the central atom, the molecular geometry of BCl3 is trigonal planar.
- Answer CO32-
-
1. The central atom, carbon, has four valence electrons, and each oxygen atom has six valence electrons. The Lewis electron structure of one of three resonance forms is represented as
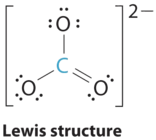
2. The structure of CO32− is a resonance hybrid. It has three identical bonds, each with a bond order of \(1 \frac{1}{3}\). All electron groups are bonds. With three bonding groups around the central atom, the structure is designated as AX3.
3. We minimize repulsions by placing the three groups 120° apart (Table \(\PageIndex{1}\)).
4. We see from Table \(\PageIndex{1}\) that the molecular geometry of CO32− is trigonal planar with bond angles of 120°.
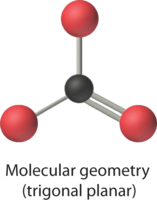
In our next example we encounter the effects of lone pairs and multiple bonds on molecular geometry for the first time.
Exercise \(\PageIndex{3}\)
Predict the geometry around the central atom in CH4, PCl5 and SF6.
- Answer CH4
-
1. The central atom, carbon, contributes four valence electrons, and each hydrogen atom has one valence electron, so the full Lewis electron structure is
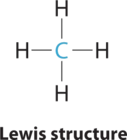
2. There are four electron groups around the central atom. All electron groups are bonding pairs, so the structure is designated as AX4.
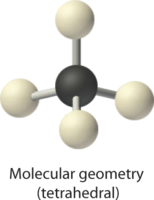
3. As shown in Table \(\PageIndex{1}\), repulsions are minimized by placing the groups in the corners of a tetrahedron with bond angles of 109.5°.
4. With four bonding pairs, the molecular geometry of methane is tetrahedral (Table \(\PageIndex{1}\)).
- Answer PCl5
-
1. Phosphorus has five valence electrons and each chlorine has seven valence electrons, so the Lewis electron structure of PCl5 is
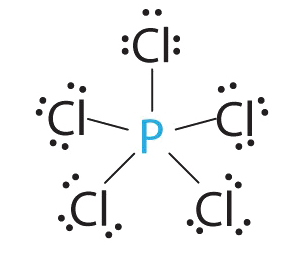
2. There are five bonding groups around phosphorus, the central atom. All electron groups are bonds, so the structure is designated as AX5.
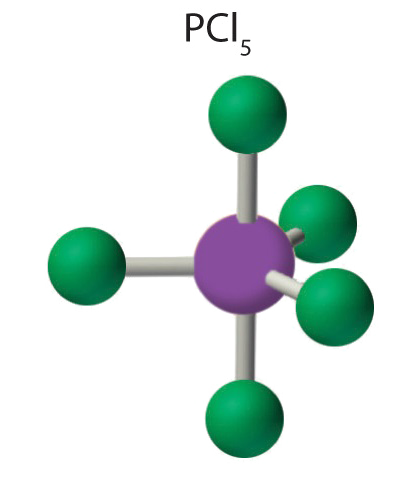
3. The structure that minimizes repulsions is a trigonal bipyramid, which consists of two trigonal pyramids that share a base (Table \(\PageIndex{1}\)).
4. The molecular geometry of PCl5 is trigonal bipyramidal, as shown below. The molecule has three atoms in a plane in equatorial positions and two atoms above and below the plane in axial positions. The three equatorial positions are separated by 120° from one another, and the two axial positions are at 90° to the equatorial plane. The axial and equatorial positions are not chemically equivalent.
- Answer SF6
-
1. The central atom, sulfur, contributes six valence electrons, and each fluorine atom has seven valence electrons, so the Lewis electron structure is
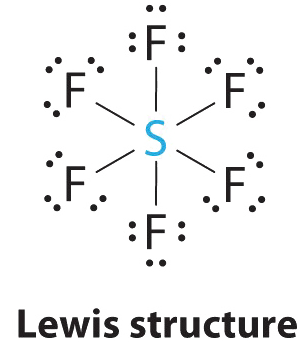
With an expanded valence, this species is an exception to the octet rule.
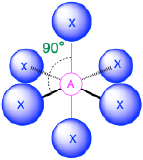
2. There are six electron groups around the central atom, each a bonding pair. We see from Figure \(\PageIndex{2}\) that the geometry that minimizes repulsions is octahedral.
3. With only bonding pairs, SF6 is designated as AX6. All positions are chemically equivalent, so all electronic interactions are equivalent.
4. There are six nuclei, so the molecular geometry of SF6 is octahedral.

Lone Pair Repulsion
In the previous section, we saw how to use VSEPR to predict the geometry around a central atom based on the number of groups attached to a central atom. However, our previous discussion was limited to the simple cases where all of the groups were bonded groups (i.e., in the designation AXmEn , n=0). When all of the groups are bonds, the geometries can be predicted using information in Table 3.2.1 in the previous section. Now we will consider cases where one or more of these groups are lone pairs.
Lone pairs have stronger repulsive forces than bonded groups.
When one or more of the groups is a lone pair of electrons (non-bonded electrons), the experimentally-observed geometry around an atom is slightly different than in the case where all groups are bonds. The actual bond angles are similar, but not exactly the same, as those predicted based on the total number of groups (the "parent" geometry). When there is a mixture of group types (lone pairs (E) and bonded groups (X)) there are three different types of angles to consider: bond angles between two bonded atoms (X-X angles), angles between a bonded atom and a lone pair (X-E angles), and angles between two lone pairs (E-E angles). Empirical evidence shows the following trend in the degree of bond angles around atoms with a mixture of group types:
Trend in bond angles:
E-E >X-E >X-X
Using empirical evidence as a guide, we can predict that lone pairs repel other electron groups more strongly than bonded pairs. The molecular geometry of molecules with lone pairs of electrons is better predicted when we consider that electronic repulsion created by lone pairs is stronger than the repulsion from bonded groups. It is difficult to predict the exact bond angle based on this principle, but we can predict approximate angles, as described and summarized below in Table \(\PageIndex{1}\).
| Electron Groups (m + n) | |||||
|---|---|---|---|---|---|
|
2 (steric number = 2) |
3 (steric number = 3) |
4 (steric number = 4) |
5 (steric number = 5) |
6 (steric number = 6) |
|
|
Parent Geometry (0 lone pairs) AXm |
AX2, linear 180° |
AX3, trig. plane 120° |
AX4, tetrahedron 109.5° |
AX5, trig. bipyramid 90°, 120° |
AX6, octahedron 90° |
|
1 lone pair AXmE1 |
AX2E1, bent <120° |
AX3E1, trig. pyramid <109.5° |
AX4E1, see-saw <90°, <120° |
AX5E1, square pyramid 90°, <90° |
|
|
2 lone pairs AXmE2 |
AX2E2, bent <109.5° |
AX3E2, T-shape <90° |
AX4E2, square plane 90° |
||
|
3 lone pairs AXmE3 |
AX2E3, linear 180° |
||||
Table \(\PageIndex{1}\) summarizes the geometries and bond angles predicted for nearest-neighbor bonded groups on central atoms with a mixture of lone pairs and bonded groups. The table does not cover all possible situations; it only includes cases where there are two bonded groups in which an X-X angle is measurable between nearest-neighbors. A more detailed description of some selected cases is given below.
Two Electron Groups (m + n = 2)
(Steric number = 2) In the case that there are only two electron groups around a central atom, those groups will lie 180° from one another. This results in a linear molecular geometry with 180° bond angles.
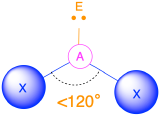
Three Electron Groups (m + n = 3)
(Steric number = 3) In the case that there are three electron groups around a central atom, those groups will lie approximately 120° from one another in space. This results in an electronic geometry that is approximately trigonal planar. There are two different molecular geometries that are possible in this category:
- When all of the electron groups are bonds (m = 3 or AX3), the molecular geometry is a trigonal plane with 120° bond angles.
- When there is one lone pair (m=2, n=1 or AX2E1), the molecular geometry is bent with a bond angle that is slightly less than 120°.
AX2E Molecules: Example SO2
1. The central atom, sulfur, has 6 valence electrons, as does each oxygen atom. With 18 valence electrons, the Lewis electron structure is shown below.
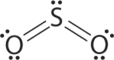
2. There are three electron groups around the central atom: two double bonds and one lone pair. We initially place the groups in a trigonal planar arrangement to minimize repulsions (Table \(\PageIndex{1}\)).
3. With two bonding pairs and one lone pair, the structure is designated as AX2E. This designation has a total of three electron pairs, two X and one E. The lone pair occupies more space around the central atom than a bonding pair (even double bonds!). Bonding pairs and lone pairs repel each other electrostatically in the order BP–BP < LP–BP < LP–LP. In SO2, we have one BP–BP interaction and two LP–BP interactions.
4. The molecular geometry is described only by the positions of the nuclei, not by the positions of the lone pairs. Thus, with two nuclei and one lone pair the shape is bent, or V shaped, which can be viewed as a trigonal planar arrangement with a missing vertex. The O-S-O bond angle is expected to be less than 120° because of the extra space taken up by the lone pair.
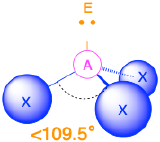
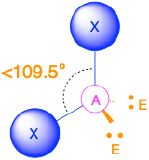
Four Electron Groups (m + n = 4)
(Steric number = 4) In the case that there are four electron groups around a central atom, those groups will lie approximately 109.5° from one another in space. This results in an electronic geometry that is approximately tetrahedral. There are three different molecular geometries that are possible in this category:
- When all electron groups are bonds (m=4 or AX4), the molecular geometry is a tetrahedron with bond angles of 109.5°.
- When there is one lone pair (m=3, n=1 or AX3E1), the molecular geometry is a trigonal pyramid with bond angles of slightly less than 109.5°.
- When there are two lone pairs (m=2, n=2 or AX2E2), the molecular geometry is bent with bond angles of slightly less than 109.5°.
AX3E Molecules: Example NH3
One of the limitations of Lewis structures is that they depict molecules and ions in only two dimensions. With four electron groups, we must learn to show molecules and ions in three dimensions.
1. In ammonia, the central atom, nitrogen, has five valence electrons and each hydrogen donates one valence electron, producing the Lewis electron structure
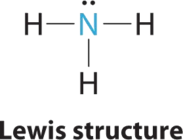
2. There are four electron groups around nitrogen, three bonding pairs and one lone pair. Repulsions are minimized by directing each hydrogen atom and the lone pair to the corners of a tetrahedron.
3. With three bonding pairs and one lone pair, the structure is designated as AX3E. This designation has a total of four electron pairs, three X and one E. We expect the LP–BP interactions to cause the bonding pair angles to deviate significantly from the angles of a perfect tetrahedron.

The Difference in the Space Occupied by a Lone Pair of Electrons and by a Bonding Pair
As with SO2, this composite model of electron distribution and negative electrostatic potential in ammonia shows that a lone pair of electrons occupies a larger region of space around the nitrogen atom than does a bonding pair of electrons that is shared with a hydrogen atom.
4. There are three nuclei and one lone pair, so the molecular geometry is trigonal pyramidal. In essence, this is a tetrahedron with a vertex missing. However, the H–N–H bond angles are less than the ideal angle of 109.5° because of LP–BP repulsion. The bond angles in ammonia are 106.6°.
AX2E2 Molecules: Example H2O
1. Oxygen has six valence electrons and each hydrogen has one valence electron, producing the Lewis electron structure
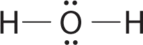
2. There are four groups around the central oxygen atom, two bonding pairs and two lone pairs. Repulsions are minimized by directing the bonding pairs and the lone pairs to the corners of a tetrahedron.
3. With two bonding pairs and two lone pairs, the structure is designated as AX2E2 with a total of four electron pairs. Due to LP–LP, LP–BP, and BP–BP interactions, we expect a significant deviation from idealized tetrahedral angles.
4. With two hydrogen atoms and two lone pairs of electrons, the structure has significant lone pair interactions. There are two nuclei about the central atom, so the molecular shape is bent, or V shaped, with an H–O–H angle that is even less than the H–N–H angles in NH3, as we would expect because of the presence of two lone pairs of electrons on the central atom rather than one. This molecular shape is essentially a tetrahedron with two missing vertices.

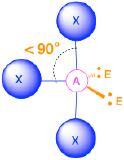
Five Electron Groups (m + n = 5)
|
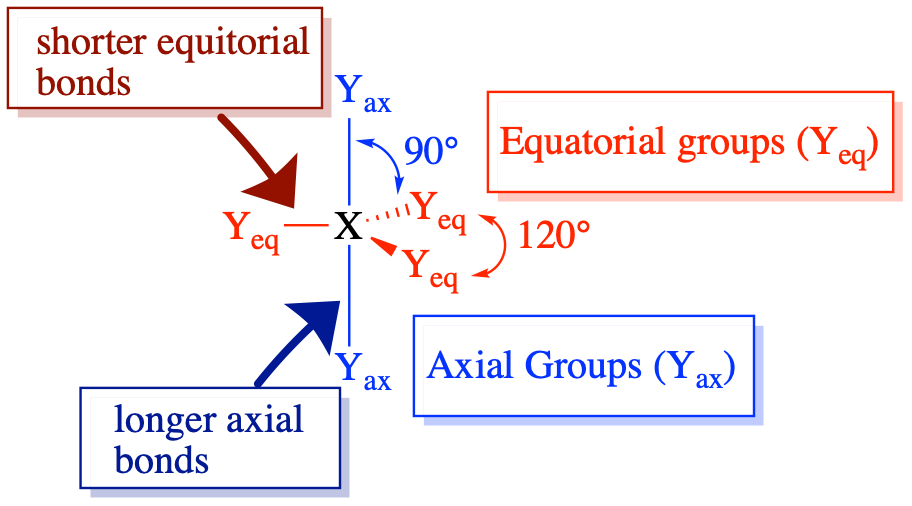
(Steric number = 5) In the case that there are five electron groups around a central atom, there are two different types of positions around the central atom: equatorial positions and axial positions. The three equatorial ligands are 120° from one another and are 90° from each of the two axial ligands. The axial positions have three adjacent groups oriented 90° away in space. Axial groups are thus more crowded than the equatorial positions with only two adjacent groups at 90°. The crowding of axial positions results in slight differences in bond distances; crowded axial groups have longer bonds than the less crowded equatorial groups. Lone pairs of electrons generally prefer to occupy equatorial positions rather than axial positions. The justification for this preference, according to VSEPR theory, is that the lone electron pairs are more repulsive than bonding electron pairs, and thus the lone pairs prefer the less crowded equatorial positions.
The arrangement of five groups around a central atom results in a trigonal bipyramidal electronic geometry. There are four different molecular geometries that are possible in this category, depending upon the number of bonded groups and lone pairs of electrons:
- When all electron groups are bonds (m=5 or AX5), the molecular geometry is a trigonal bipyramid with bond angles of 120° and 90° between adjacent ligands.
- When there is one lone pair (m=4, n=1 or AX4E1), the lone pair occupies one of the equatorial positions. The molecular geometry is called a see saw with bond angles of slightly less than 120° and slightly less than 90°.
- When there are two lone pairs (m=3, n=2 or AX3E2), each lone pair occupies one of the three equatorial positions. The molecular geometry is T-shaped with bond angles of slightly less than 120° and slightly less than 90°.
- When there are three lone pairs (m=1, n=3 or AX3E2), the lone pairs occupy the three equatorial positions. The molecular geometry is linear with bond angles of 180°.
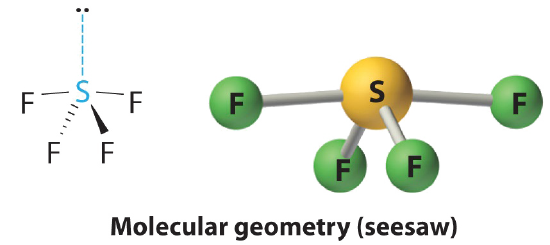
AX4E Molecules: SF4
1. The sulfur atom has six valence electrons and each fluorine has seven valence electrons, so the Lewis electron structure is

With an expanded valence, this species is an exception to the octet rule.
2. There are five groups around sulfur, four bonding pairs and one lone pair. With five electron groups, the lowest energy arrangement is a trigonal bipyramid.
3. We designate SF4 as AX4E; it has a total of five electron pairs. However, because the axial and equatorial positions are not chemically equivalent, where do we place the lone pair? If we place the lone pair in the axial position, we have three LP–BP repulsions at 90°. If we place it in the equatorial position, we have two 90° LP–BP repulsions at 90°. With fewer 90° LP–BP repulsions, we can predict that the structure with the lone pair of electrons in the equatorial position is more stable than the one with the lone pair in the axial position. We also expect a deviation from ideal geometry because a lone pair of electrons occupies more space than a bonding pair.
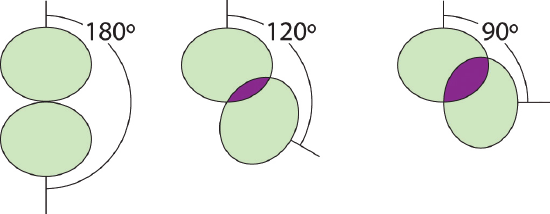
Illustration of the Area Shared by Two Electron Pairs versus the Angle between Them
At 90°, the two electron pairs share a relatively large region of space, which leads to strong repulsive electron–electron interactions.
4. With four nuclei and one lone pair of electrons, the molecular structure is based on a trigonal bipyramid with a missing equatorial vertex; it is described as a seesaw. The Faxial–S–Faxial angle is 173° rather than 180° because of the lone pair of electrons in the equatorial plane.
AX3E2 Molecules: BrF3
1. The bromine atom has seven valence electrons, and each fluorine has seven valence electrons, so the Lewis electron structure is
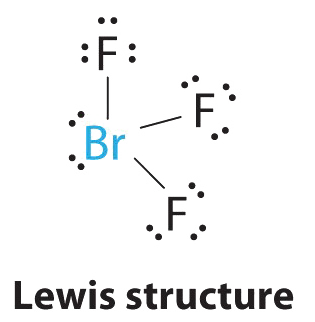
Once again, we have a compound that is an exception to the octet rule.
2. There are five groups around the central atom, three bonding pairs and two lone pairs. We again direct the groups toward the vertices of a trigonal bipyramid.
3. With three bonding pairs and two lone pairs, the structural designation is AX3E2 with a total of five electron pairs. Because the axial and equatorial positions are not equivalent, we must decide how to arrange the groups to minimize repulsions. If we place both lone pairs in the axial positions, we have six LP–BP repulsions at 90°. If both are in the equatorial positions, we have four LP–BP repulsions at 90°. If one lone pair is axial and the other equatorial, we have one LP–LP repulsion at 90° and three LP–BP repulsions at 90°:
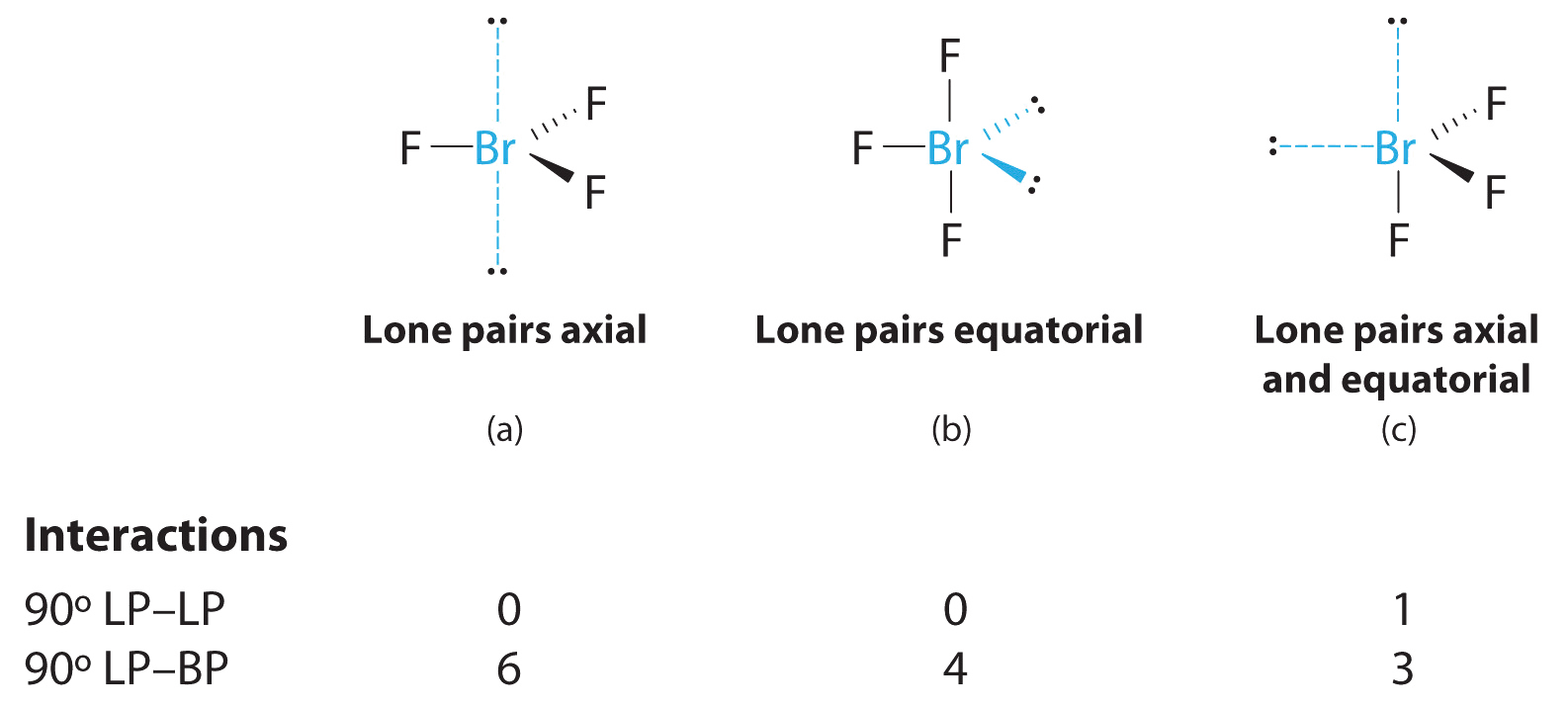
Structure (c) can be eliminated because it has a LP–LP interaction at 90°. Structure (b), with fewer LP–BP repulsions at 90° than (a), is lower in energy. However, we predict a deviation in bond angles because of the presence of the two lone pairs of electrons.
4. The three nuclei in BrF3 determine its molecular structure, which is described as T shaped. This is essentially a trigonal bipyramid that is missing two equatorial vertices. The Faxial–Br–Faxial angle is 172°, less than 180° because of LP–BP repulsions.
Because lone pairs occupy more space around the central atom than bonding pairs, electrostatic repulsions are more important for lone pairs than for bonding pairs.
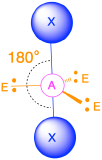
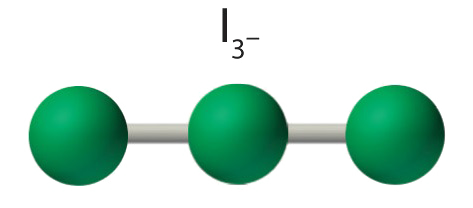
AX2E3 Molecules: I3−
1. Each iodine atom contributes seven electrons and the negative charge one, so the Lewis electron structure is
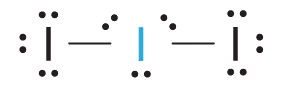
2. There are five electron groups about the central atom in I3−, two bonding pairs and three lone pairs. To minimize repulsions, the groups are directed to the corners of a trigonal bipyramid.
3. With two bonding pairs and three lone pairs, I3− has a total of five electron pairs and is designated as AX2E3. We must now decide how to arrange the lone pairs of electrons in a trigonal bipyramid in a way that minimizes repulsions. Placing them in the equatorial positions eliminates 90° LP–LP repulsions and minimizes the number of 90° LP–BP repulsions.
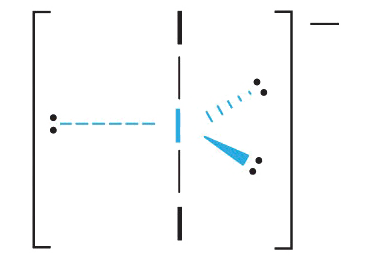
The three lone pairs of electrons have equivalent interactions with the three iodine atoms, so we do not expect any deviations in bonding angles.
4. With three nuclei and three lone pairs of electrons, the molecular geometry of I3− is linear. This can be described as a trigonal bipyramid with three equatorial vertices missing. The ion has an I–I–I angle of 180°, as expected.
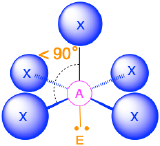
Six Electron Groups (m + n = 6)
(Steric number = 6) In the case that there are six electron groups around a central atom, the nearest groups will lie approximately 90° from one another in space. This results in an electronic geometry that is approximately octahedral. There are three relevant molecular geometries in this category:
- When all electron groups are bonds (m=6 or AX6), the molecular geometry is an octahedron with bond angles of 90° between adjacent bonds.
- When there is one lone pair (m=5, n=1 or AX5E1) we now distinguish between the axial and equitorial positions; the lone pair is considered to be in one of the axial positions, while the bond directly opposite of the lone pair is the axial bond. The molecular geometry is a square pyramid with bond angles of 90° between adjacent equatorial bonds and slightly less than 90° between the axial bond and equatorial groups.
- When there are two lone pairs (m=4, n=2 or AX4E2), the lone pairs are opposite of one another and each occupy an axial position. The molecular geometry is square planar with bond angles of 90°.
AX5E Molecules: BrF5
1. The central atom, bromine, has seven valence electrons, as does each fluorine, so the Lewis electron structure is
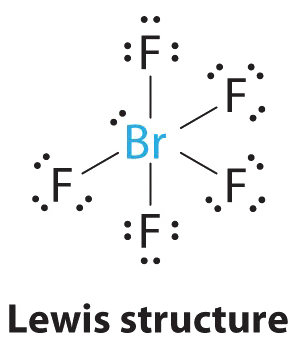
With its expanded valence, this species is an exception to the octet rule.
2. There are six electron groups around the Br, five bonding pairs and one lone pair. Placing five F atoms around Br while minimizing BP–BP and LP–BP repulsions gives the following structure:
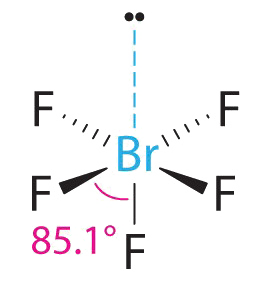
3. With five bonding pairs and one lone pair, BrF5 is designated as AX5E; it has a total of six electron pairs. The BrF5 structure has four fluorine atoms in a plane in an equatorial position and one fluorine atom and the lone pair of electrons in the axial positions. We expect all Faxial–Br–Fequatorial angles to be less than 90° because of the lone pair of electrons, which occupies more space than the bonding electron pairs.
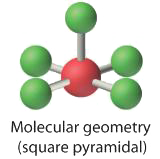
4. With five nuclei surrounding the central atom, the molecular structure is based on an octahedron with a vertex missing. This molecular structure is square pyramidal. The Faxial–B–Fequatorial angles are 85.1°, less than 90° because of LP–BP repulsions.
AX4E2 Molecules: ICl4−
1. The central atom, iodine, contributes seven electrons. Each chlorine contributes seven, and there is a single negative charge. The Lewis electron structure is

2. There are six electron groups around the central atom, four bonding pairs and two lone pairs. The structure that minimizes LP–LP, LP–BP, and BP–BP repulsions is
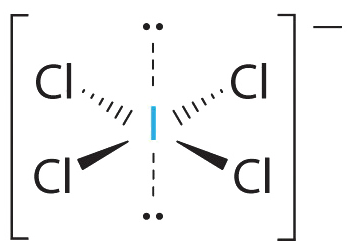
3. ICl4− is designated as AX4E2 and has a total of six electron pairs. Although there are lone pairs of electrons, with four bonding electron pairs in the equatorial plane and the lone pairs of electrons in the axial positions, all LP–BP repulsions are the same. Therefore, we do not expect any deviation in the Cl–I–Cl bond angles.
4. With five nuclei, the ICl4− ion forms a molecular structure that is square planar, an octahedron with two opposite vertices missing.
Summary
The arrangement of bonded atoms in a molecule or polyatomic ion is crucial to understanding the chemistry of a molecule, but Lewis electron structures give no information about molecular geometry. The valence-shell electron-pair repulsion (VSEPR) model allows us to predict which of the possible structures is actually observed in most cases. VSEPR is based on the assumption that pairs of electrons occupy space, and the lowest-energy structure is the one that minimizes repulsions between electron pairs. In the VSEPR model, the molecule or polyatomic ion is given an AXmEn designation, where A is the central atom, X is a bonded atom, E is a nonbonding valence electron group (usually a lone pair of electrons), and m and n are integers. Each group around the central atom is designated as a bonding pair (BP) or lone (nonbonding) pair (LP). From the BP and LP interactions we can predict both the relative positions of the atoms and the angles between the bonds, called the bond angles. From this we can describe the molecular geometry. The VSEPR model can be used to predict the shapes of many molecules and polyatomic ions, but it gives no information about bond lengths and the presence of multiple bonds. A combination of VSEPR and a bonding model, such as Lewis electron structures, is necessary to understand the presence of multiple bonds.
The relationship between the number of electron groups around a central atom, the number of lone pairs of electrons, and the molecular geometry is summarized in Table \(\PageIndex{1}\).
Example Excercises
Example \(\PageIndex{1}\)
Using the VSEPR model, predict the molecular geometry of each molecule or ion.
- PF5 (phosphorus pentafluoride, a catalyst used in certain organic reactions)
- H3O+ (hydronium ion)
Given: two chemical species
Asked for: molecular geometry
Strategy:
- Draw the Lewis electron structure of the molecule or polyatomic ion.
- Determine the electron group arrangement around the central atom that minimizes repulsions.
- Assign an AXmEn designation; then identify the LP–LP, LP–BP, or BP–BP interactions and predict deviations in bond angles.
- Describe the molecular geometry.
Solution:
- A The central atom, P, has five valence electrons and each fluorine has seven valence electrons, so the Lewis structure of PF5 is
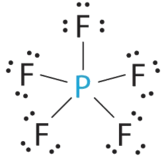
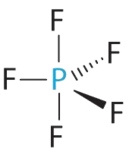
B There are five bonding groups about phosphorus. The structure that minimizes repulsions is a trigonal bipyramid.
C All electron groups are bonding pairs, so PF5 is designated as AX5. Notice that this gives a total of five electron pairs. With no lone pair repulsions, we do not expect any bond angles to deviate from the ideal.
D The PF5 molecule has five nuclei and no lone pairs of electrons, so its molecular geometry is trigonal bipyramidal.
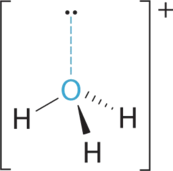
- A The central atom, O, has six valence electrons, and each H atom contributes one valence electron. Subtracting one electron for the positive charge gives a total of eight valence electrons, so the Lewis electron structure is
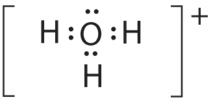
B There are four electron groups around oxygen, three bonding pairs and one lone pair. Like NH3, repulsions are minimized by directing each hydrogen atom and the lone pair to the corners of a tetrahedron.
C With three bonding pairs and one lone pair, the structure is designated as AX3E and has a total of four electron pairs (three X and one E). We expect the LP–BP interactions to cause the bonding pair angles to deviate significantly from the angles of a perfect tetrahedron.
D There are three nuclei and one lone pair, so the molecular geometry is trigonal pyramidal, in essence a tetrahedron missing a vertex. However, the H–O–H bond angles are less than the ideal angle of 109.5° because of LP–BP repulsions:
Exercise \(\PageIndex{1}\)
Using the VSEPR model, predict the molecular geometry of each molecule or ion.
- XeO3
- PF6−
- NO2+
- Answer a
-
trigonal pyramidal
- Answer b
-
octahedral
- Answer c
-
linear
Example \(\PageIndex{2}\)
Predict the molecular geometry of each molecule.
- XeF2
- SnCl2
Given: two chemical compounds
Asked for: molecular geometry
Strategy:
Use the strategy given in Example\(\PageIndex{1}\).
Solution:
- A Xenon contributes eight electrons and each fluorine seven valence electrons, so the Lewis electron structure is

B There are five electron groups around the central atom, two bonding pairs and three lone pairs. Repulsions are minimized by placing the groups in the corners of a trigonal bipyramid.
C From B, XeF2 is designated as AX2E3 and has a total of five electron pairs (two X and three E). With three lone pairs about the central atom, we can arrange the two F atoms in three possible ways: both F atoms can be axial, one can be axial and one equatorial, or both can be equatorial:
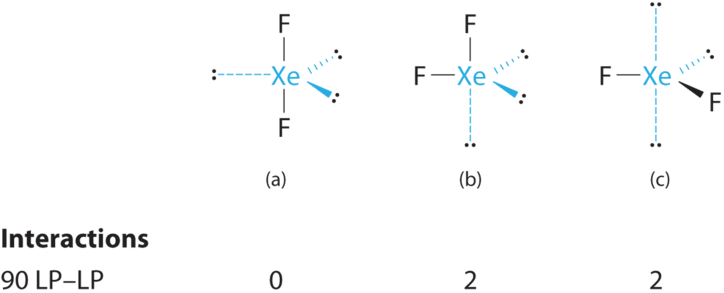
The structure with the lowest energy is the one that minimizes LP–LP repulsions. Both (b) and (c) have two 90° LP–LP interactions, whereas structure (a) has none. Thus both F atoms are in the axial positions, like the two iodine atoms around the central iodine in I3−. All LP–BP interactions are equivalent, so we do not expect a deviation from an ideal 180° in the F–Xe–F bond angle.
D With two nuclei about the central atom, the molecular geometry of XeF2 is linear. It is a trigonal bipyramid with three missing equatorial vertices.
- A The tin atom donates 4 valence electrons and each chlorine atom donates 7 valence electrons. With 18 valence electrons, the Lewis electron structure is
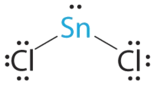
B There are three electron groups around the central atom, two bonding groups and one lone pair of electrons. To minimize repulsions the three groups are initially placed at 120° angles from each other.
C From B we designate SnCl2 as AX2E. It has a total of three electron pairs, two X and one E. Because the lone pair of electrons occupies more space than the bonding pairs, we expect a decrease in the Cl–Sn–Cl bond angle due to increased LP–BP repulsions.
D With two nuclei around the central atom and one lone pair of electrons, the molecular geometry of SnCl2 is bent, like SO2, but with a Cl–Sn–Cl bond angle of 95°. The molecular geometry can be described as a trigonal planar arrangement with one vertex missing.
Exercise \(\PageIndex{2}\)
Predict the molecular geometry of each molecule.
- SO3
- XeF4
- Answer a
-
trigonal planar
- Answer b
-
square planar