0.1.2.1: How to predict most electron configurations
- Page ID
- 195422
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Predicting electron configuration with the Aufbau Principle
The Aufbau Principle (also called the building-up principle or the Aufbau rule) allows us to reliably predict the ground state electron configuration of atoms and ions. The Aufbau principle states that, in the ground state of an atom or ion, electrons fill atomic orbitals of the lowest available energy level before occupying higher-energy levels.
To apply the Aufbau principle, you must know the relative energy levels of all atomic orbitals. In general (*most* cases), atomic orbital energy level increases as the values of quantum numbers increase, in the following order of priority: \(n\) and \(l\). We usually assume that orbitals within a subshell are degenerate, but convention is to assign the lowest values of \(m_l\) first within any subshell. The value of the quantum number, \(m_s\), for an unpaired electron is conventionally assigned a value of \(+\frac{1}{2}\).
The Ground State of Hydrogen (and Hydrogenic Atoms/Ions)
In hydrogen (or a hydrogenic atom/ion), there is only one electron. In this case, the only factor determining energy is the value of \(n\). The ground state will always be the 1s orbital (\(n=1, l=0, m_l=0, m_s=+\frac{1}{2}\)).
The Ground State of Multi-electron Atoms/Ions
Most of the atoms and ions you will be dealing with are multi-electron species. In atoms/ions with two or more electrons, the ground state electron configuration must (1) minimize the total energy of the electrons, (2) obey the Pauli exclusion principle (3) obey Hunds rule of maximum multiplicity, and (4) consider the exchange interaction. These "rules" are described below in Table \(\PageIndex{1}\).
|
(1) Electrons will occupy the lowest energy orbitals in order to minimize the total energy. The two quantum numbers that are related to energy in multi-electron atoms are \(n\), and \(l\). Thus, orbitals with the lowest values of \(n\) and \(l\) will fill first. **This order of filling works most of the time, but not always. It always works for main group elements, but it only occasionally works for transition metals. Why? Well, as we increase in values of \(n\), the orbital energy levels get closer and closer together. At the point that we're at the \(n=3\) and \(n=4\) shells (the transition metals!), things start to cross over so that some \(n=4\) orbitals are lower in energy than some of the \(n=3\) orbitals! But, in all transition metals, the 3d orbital is slightly lower in energy than 4s. The 3d orbital becomes lower and lower in energy relative to 4s as we go across the periodic table. This closeness of energy levels from different shells is one of the reasons why transition metals have such interesting properties. |
Figure \(\PageIndex{1}\). The order of filling of ground state electron orbitals is 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, etc... (CC-BY-NC-SA; Kathryn Haas) |
|
(2) Hund's rule of maximum multiplicity states that for a given electron configuration, the lowest energy arrangement of electrons in degenerate orbitals is the one with the greatest "multiplicity", where the multiplicity is the number of unpaired electrons (n)** plus 1 (multiplicity = n + 1). This rule is used to predict the ground state of an atom or molecule with one or more open electronic shells. Hund's rule is based on empirical observation of atomic spectra, and it is a consequence of the energy required to pair two electrons in the same orbital. This energy of repulsion between two electrons in the same orbitals is a Coulombic energy of repulsion, \(\Pi_c\), caused by two electrons with like charge sharing the same area of space (an orbital). When more than one electron occupies a set of degenerate orbitals, the most favorable arrangement is one where the number of paired electrons is minimized. A simplified definition of Hund's rule is that the lowest energy arrangement is the one with the greatest number of unpaired electrons. This implies that if two or more orbitals of equal energy are available, electrons will occupy them singly before filling them in pairs. Examples of ground state arrangements of electrons in three degenerate p-orbitals is given in the figure shown here. **This is not the same "\(n\)" we saw for the principle quantum number. |
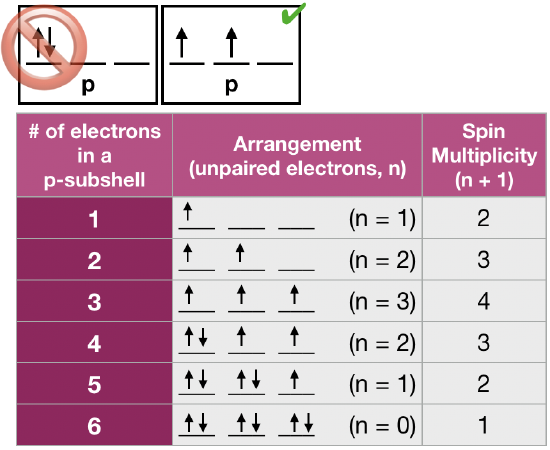 Figure \(\PageIndex{2}\) Hund's rule is that spin multiplicity must be maximized in the ground state. (CC-BY-NC-SA; Kathryn Haas) Figure \(\PageIndex{2}\) Hund's rule is that spin multiplicity must be maximized in the ground state. (CC-BY-NC-SA; Kathryn Haas) |
|
(3) The Pauli exclusion principle states that it is impossible for two electrons of a multi-electron atom to have the same set of values for the four quantum numbers. Two electrons in different orbitals will have a different set of \(n, l\), and \(m_l\) values. When two electrons reside in the same orbital, they posses the same \(n, l\), and \(m_l\) values, therefore their ms must be different. Thus two electrons in the same orbital must have opposite half-integer spin projections of \(+\frac{1}{2}\) and \(-\frac{1}{2}\). |
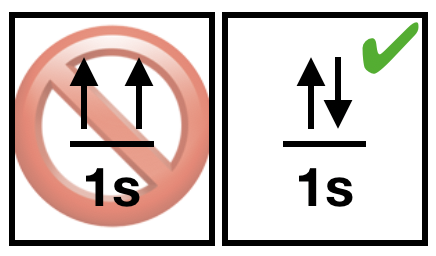 Figure \(\PageIndex{3}\). Pauli's principle tells us that paired electrons must have opposite spin. (CC-BY-NC-SA; Kathryn Haas) Figure \(\PageIndex{3}\). Pauli's principle tells us that paired electrons must have opposite spin. (CC-BY-NC-SA; Kathryn Haas) |
|
(4) The exchange interaction is sometimes called the exchange energy or exchange force, however it is not a true energy or force. Rather, it is a quantum mechanical effect that takes place between identical particles. The exchange interaction results in a ground state electron configuration with unpaired electrons all being of the same spin. It is convention to write the unpaired electrons in the "spin up" direction. |
|
Reading valence count and electron configuration from the periodic table
The periodic table is a helpful tool for predicting chemical and physical properties of the elements. It is divided into Groups (columns) and Periods (rows). The Groups are characterized by similar atomic valence electron configuration, while periods are characterized by the atomic valence shell. My favorite periodic table (especially for this course!) is available for download and printing on sciencenotes.com (click here). I strongly encourage you to download the high resolution image in the color scheme of your choice, print it out, and keep it close as a handy reference. I love this periodic table because it is attractive and useful, and especially because it has the electron configurations for every element listed clearly along with other information like atomic number and average mass.
Because the periodic table is organized into groups and columns, it is rather simple to predict electron configuration from a simple glance. You should already be familiar with predicting electron configurations from your previous chemistry courses (brush up now if necessary!). Figure \(\PageIndex{6}\) below illustrates that finding the valence count is as easy as counting blocks from left to right across the table. And to find the ground state valence electron configuration, you simply need to know where the s, p, d, and f blocks are (Figure \(\PageIndex{6}\)). For example, you should be able to predict that carbon (C) has 6 valence electrons and that it's ground state electron configuration is 1s22s22p2 by looking at any periodic table.

Figure \(\PageIndex{5}\). This is a depiction of the periodic table, and how its arrangement can tell you the valence count of any atom. The valence of an ion can be extrapolated from the electron count of the analogous atom.
Trends in Expected Electron Configuration of Atoms
The four "rules" described in Table \(\PageIndex{1}\) can be used as guidelines for predicting the ground state electron configuration of atoms, the filling of subshells, and the configuration of electrons in degenerate orbitals. However, the utility of these guidelines for predicting actual electron configurations requires more nuanced knowledge of the relative energy levels of orbitals.
It is generally true that orbital energy levels directly correspond to their shell number. It is also generally true that orbitals within a shell follow the energetic trend where s<p<d<f. Although these general trends hold true for most of the main block elements (the s - and p-blocks), there are important exceptions in the orbital energy levels of transition metal atoms and ions of the d- and f-blocks.
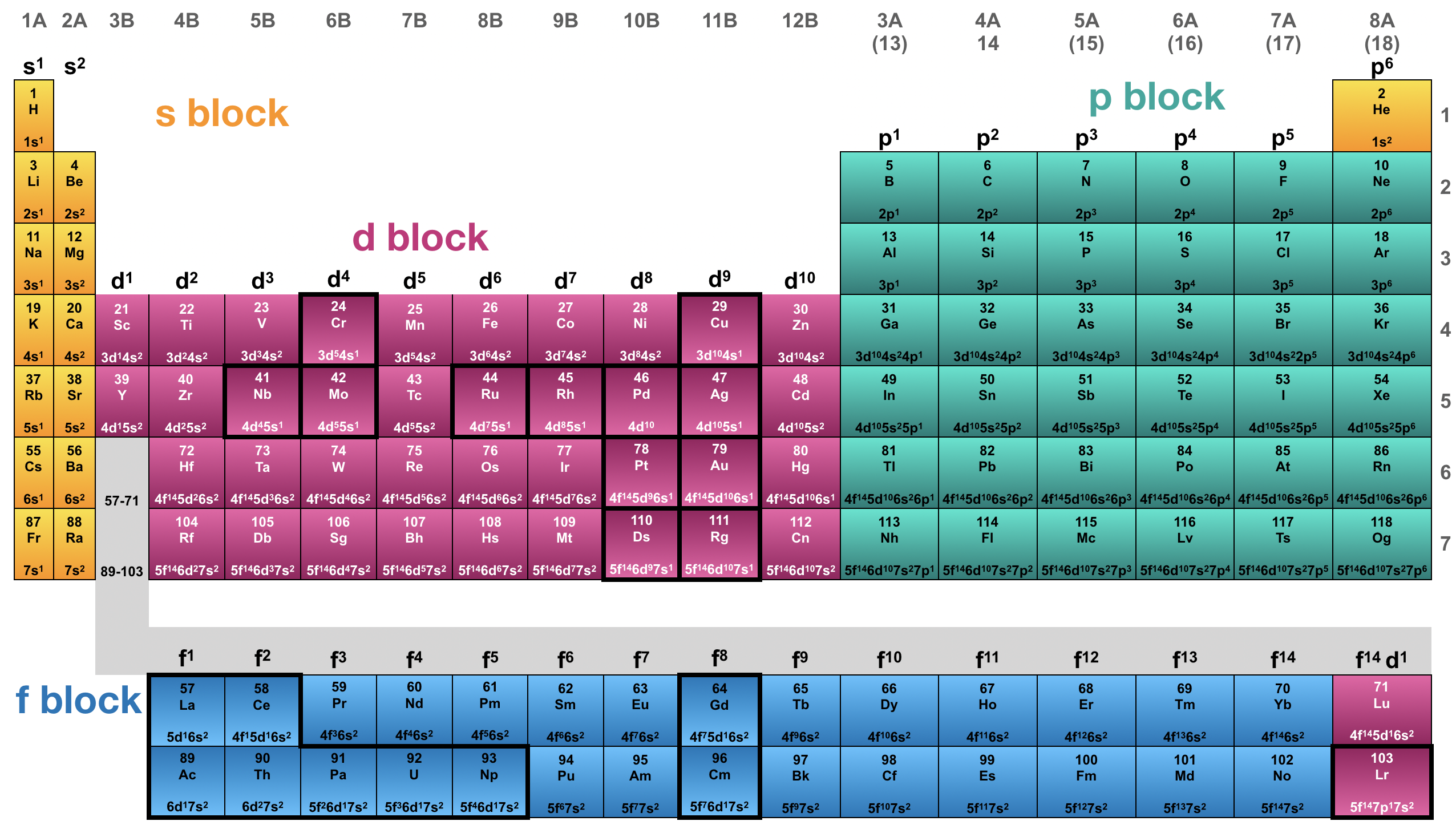
Figure \(\PageIndex{6}\). This is a depiction of the periodic table that highlights the s-, p-, d-, and f- blocks in different colors. Violations of the expected trend in electron configurations are outlined in a heavy black line. Several elements of the d block and f block violate the general trends in electron configuration because their orbital energy levels do not follow general trends. (CC-BY-NC-SA; Kathryn Haas)
Elements that violate general trends in electron configuration are outlined with a dark line in Figure \(\PageIndex{6}\). Please notice that all of the exceptions are within the d- and f- blocks. These exceptions (or violations to the normal rule) are not violation of the Aufbau principle, but rather, are caused by an unexpected order of the orbital energy levels and/or additional energetic factors. Please take note of the elements Cr and Cu, and their unexpected electron configurations (shown in small font in Figure \(\PageIndex{6}\)). Part of the explanation for the unusual electron configurations of Cr and Cu is that there is a special energy benefits to having either a half-filled or fully-filled d-subshell.
Electron Configurations of Ions
The electron configurations of ions can be derived from the electron configuration of the corresponding atom. I assume you already know how to derive an ion by adding or subtracting electrons from atoms to make the appropriate positively or negatively charged elemental ion.
Electron Configurations of (-) negative ions: When "adding" electrons to make a negative ion, we add those "extra" electrons to the lowest-energy orbital that is empty or partially-filled in the atom (still following rules from Table \(\PageIndex{1}\)).
Electron Configurations of (+) positive ions: When "removing" electrons from the atom to make a positively charged ion, the electrons are removed from the highest-energy orbital that is filled or partially filled (again, still following rules from Table \(\PageIndex{1}\)). This is where things can be a bit counterintuitive to the novice inorganic chemistry student. Positively charged transition metal ions NEVER have electrons in the valence shell s-orbital! This is because when electrons are removed from transition metal ions, it causes a drop in the 3d-orbital energy level relative to the 4s. The example below is meant to illustrate this point.
Write the valence electron configuration of Ti and Ti1+.
Solution
Titanium (Ti) is in group 4, thus it has 4 valence electrons. If we use the periodic table as a guide, we can predict that two of the electrons would reside in the 4s orbital, and two of the electrons would reside in the 3d orbital. The valence electron configuration for Titanium is [Ar] 4s23d2. A more correct way to write this is [Ar] 3d24s2 because the 3d orbital is actually lower in energy than 4s in this element.
We know that the 4s orbital is the highest-energy occupied orbital, so we should remove one electron from this orbital to form the (+1) ion. However, upon formation of the (+1) ion, the 3d energy level drops even more relative to the 4s orbital. Therefore, the one electron that would be in 4s moves to the lower-energy 3d orbital. This gives us the correct electron configuration for Ti1+: [Ar] 3d3. Another correct way to write this is [Ar] 3d34s0
Exercises
Please check your understanding by completing the problems below.
- Write the electron configurations of the following atoms (write orbitals in order of increasing energy):
A) Oxygen B) Zinc C) Copper D) Iron E) Calcium F) Cr - Write the electron configurations of the following atoms:
A) Oxygen-2 B) Zinc+2 C) Copper+1 D) Iron+2 E) Calcium+2 F) Cr+3 - Explain how and why the electron configurations of Ca and Sr atoms are almost identical.
- What is similar about all elements in group 1?
- What is similar about all elements in period 3?
- Answer 1
-
*Orbitals have been written in order of increasing energy. You should practice following this convention.
A) [He]2s22p4 B) [Ar]3d104s2 C) *[Ar]3d104s1 D) [Ar]3d64s2 E) [Ar]4s2 F) *[Ar] 3d54s1 - Answer 2
-
*Orbitals should been written in order of increasing energy:
A) [He]2s22p6 B) [Ar]3d10 C) [Ar]3d10 D) [Ar]3d6 E) [Ar] F) [Ar]3d3 - Answer 3
-
Ca and Sr are both in group 2. They have similar valence electron configurations in that their valence shell has two electrons in an s orbital. Both have the configuration [noble gas]ns2. All group 2 elements have this same electron configuration because of the repeating patterns in atomic structure and the organization of the periodic table in which atoms with similar structure are grouped together.
- Answer 4
-
All elements in group 1 have one valence electron in the valence s orbital. They would also make +1 ions.
- Answer 5
-
All elements in period 3 have n=3 as their valence shell.
If you struggle to answer any of these questions, you should study material located in a General Chemistry Text. The only one that should have been a bit tricky is question 1C. The electron configuration of copper is an exception to general trends, and you can read on to learn why it is an exception. From now on out, I'll assume that you know how to predict electron configurations of the main group elements from the periodic table. And, as you move forward, you'll also need to learn how to predict electron configurations of the transition metals. The transition metals have some interesting nuances that causes exceptions to the general trends you learned in lower-level chemistry courses. You will learn about this in the next few pages.
References
- Miessler, Gary L., and Donald A. Tarr. Inorganic Chemistry. Upper Saddle River, NJ: Pearson Prentice Hall, 2010. Print.
-
Brown, Ian David. The Chemical Bond in Inorganic Chemistry the Bond Valence Model. Oxford: Oxford UP, 2006. Print.



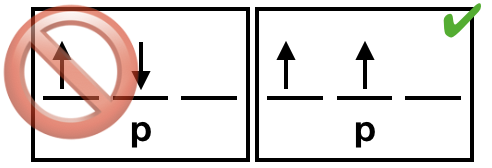 Figure \(\PageIndex{4}\). Unpaired electrons should have identical spins due to the exchange interaction. (CC-BY-NC-SA; Kathryn Haas)
Figure \(\PageIndex{4}\). Unpaired electrons should have identical spins due to the exchange interaction. (CC-BY-NC-SA; Kathryn Haas)