7.1: The Fundamentals
- Page ID
- 321428
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)We have said many times before that stereochemistry is the study of molecules that have a different orientation in space. Stereoisomers arise when molecules with the same constitution (same atoms attached to the same atoms) differ in their orientation of those atoms in three-dimensional space. We have come across stereoisomers before in the form of double bond isomers, or geometric isomers.
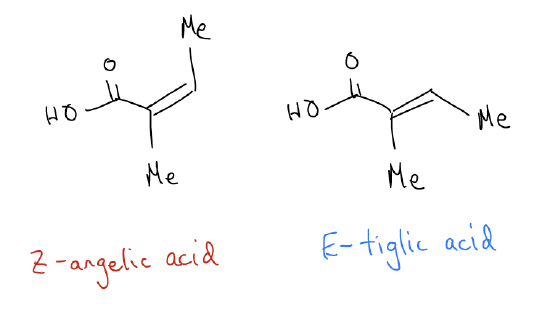
The E and Z isomers have a different orientation of the atoms attached to the double bond. Their E/Z nomenclature is determined by the priority of each group attached to the double bond, based on atomic number. Geometric isomers fall under a larger umbrella of stereoisomers called diastereomers. Diastereomers are stereoisomers that are not mirror images and not superimposable. So, they are non-superimposable, non-mirror images of each other. Z-angelic acid and E-tiglic acid are neither mirror images of each other, nor can they be superimposed on one another (that is, laid on top of each other so that all of the atoms and bonds match), so they are considered diastereomers. If they were superimposable on their mirror image, they would be the same compound!
The two molecules below, while mirror images, can superimpose on one another, so they are identical (and therefore not diastereomers). Another example of diastereomers would be the cis/trans isomers of substituted rings. cis-1,2-Cyclohexanediol and trans-1,2-cyclohexanediol are diastereomers because they are not mirror images and they cannot be superimposed.
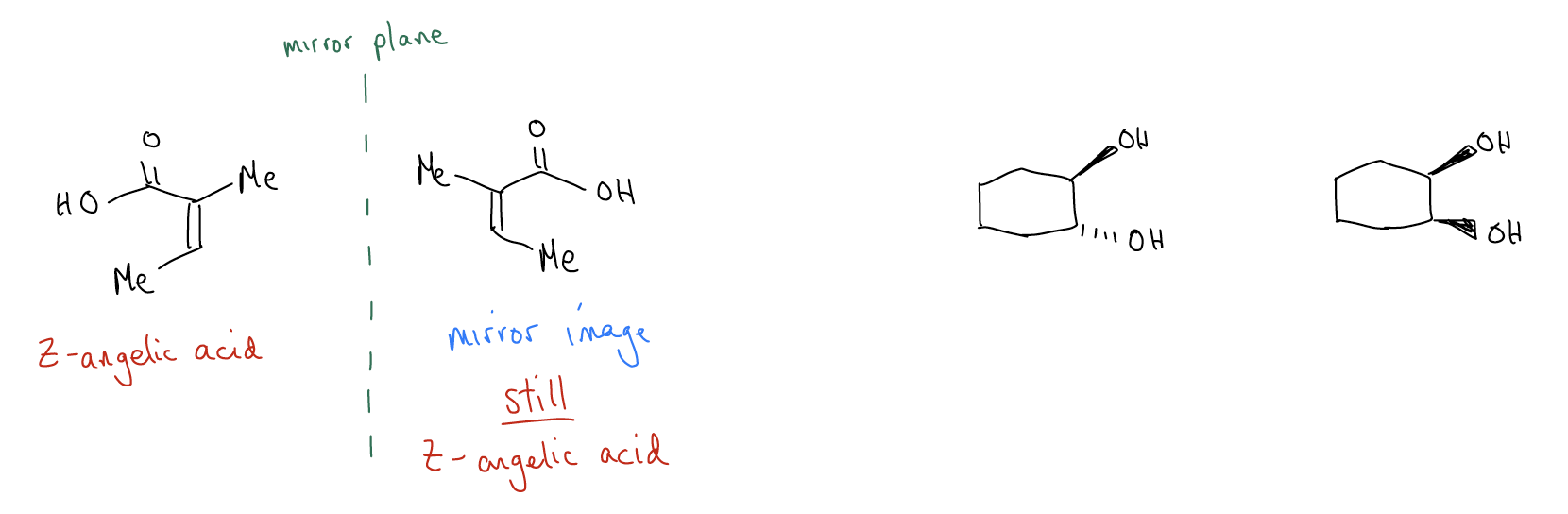
Let’s now compare the following molecules. Are they mirror images? Are they superimposable?
Species that are nonsuperimposable mirror images are another class of stereoisomers called enantiomers. Enantiomers exist everywhere in nature. Your hands, for example, are enantiomeric – they are mirror images but cannot be superimposed. While diastereomers are different compounds with different energies and physical properties (mp, bp, NMR, IR, refractive index, etc.), enantiomers have identical physical properties because they have the same energy. The only physical property that is different between enantiomers is the ability to rotate plane polarized light or circularly polarized light. Hold this thought for a moment while we discuss a few more terms.
Suppose that we have the enantiomers A and B from above. If we had a sample that contained 100% enantiomer A, we say that the sample is enantiopure. If we had a sample that contained 100% enantiomer B, we say that it is also enantiopure. If we had a sample that contained 95% of isomer A and 5% of isomer B, we say it is enantioenriched in A. The enantiomeric excess (ee) of this sample, defined as the difference between the major and minor enantiomer, would be 90%. However, if we had a sample that contained 50% A and 50% B, we have what is known as a racemic mixture (or racemate). The enantiomeric excess of a racemic mixture is 0.
Now, let’s go back to our discussion of enantiomers’ ability to rotate plane or circularly polarized light. For a sample that is 100% A, plane-polarized light passing through a sample will rotate (refract) by some value, let’s say +X (although it could be –X). The enantiopure sample of molecule B will rotate plane-polarized light by the same value, but in the opposite direction, –X. We call this the optical rotation of the sample, or α, which is measured by a polarimeter. Note that the optical rotation’s sign and magnitude are completely random (that is, nor correlation between structure and + or –), but for a pair of enantiomers, they will ALWAYS be equal in magnitude and opposite in sign.
The specific rotation is a standardized way of reporting optical rotation, which can vary from instrument to instrument. We did the same kind of thing for chemical shift in NMR. When comparing values in the literature, always compare the specific rotation values:
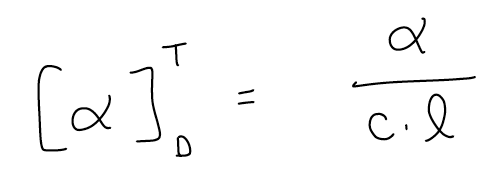
[α] = optical rotation obtained directly from the polarimeter
T = temperature
D = designation for the light source, normally a Na arc lamp.
c = concentration in g/mL
l = path length, normally in dm (10 cm).
What happens when we measure the optical rotation of a sample that is not enantiopure, but rather only enantioenriched? For example, if the optical rotation for an enantiopure sample of A is 10°, what is the optical rotation for a sample that is 95% A and 5% B? Well if the optical rotation values for enantiomers are equal and opposite, then the portion of light that is rotate to one side by the 5% B should be offset by the rotation in the opposite direction by 5% A. This leaves an excess of 90% A. What this means, then, is that the optical rotation of the mixture should be a fraction of the value for enantiopure A (this assumes that the concentration of the sample we are measuring is the same as that obtained for pure A). Indeed, the optical rotation should be:
