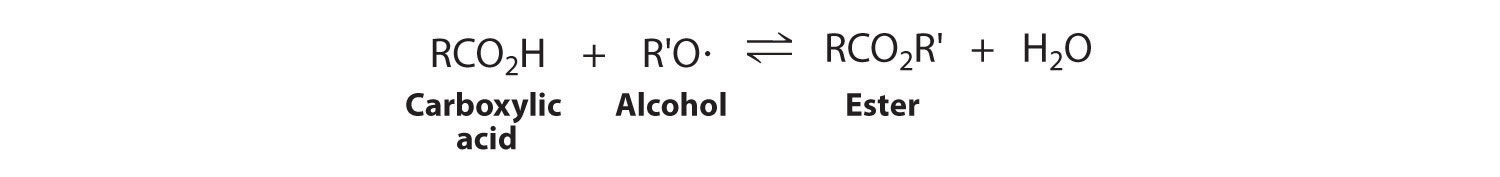Chapter 14.5: Factors That Affect Equilibrium
- Page ID
- 42122
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\) |
Prince George's Community College |
 |
| Unit I: Atoms Unit II: Molecules Unit III: States of Matter Unit IV: Reactions Unit V: Kinetics & Equilibrium Unit VI: Thermo & Electrochemistry Unit VII: Nuclear Chemistry |
||
Learning Objectives
- To predict the effects of stresses on a system at equilibrium.
Chemists use various strategies to increase the yield of the desired products of reactions. When synthesizing an ester, for example, how can a chemist control the reaction conditions to obtain the maximum amount of the desired product? Only three types of stresses can change the composition of an equilibrium mixture: (1) a change in the concentrations (or partial pressures) of the components by adding or removing reactants or products, (2) a change in the total pressure or volume, and (3) a change in the temperature of the system. In this section, we explore how changes in reaction conditions can affect the equilibrium composition of a system. We will explore each of these possibilities in turn.
Changes in Concentration
If we add a small volume of carbon tetrachloride (CCl4) solvent to a flask containing crystals of iodine, we obtain a saturated solution of I2 in CCl4, along with undissolved crystals:
\[I_{2(s)} \rightleftharpoons I_{2(soln)}\tag{14.5.1}\]
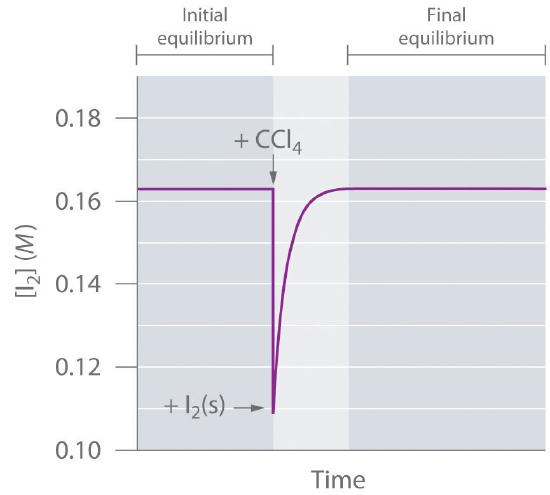
The system reaches equilibrium, with K = [I2]. If we add more CCl4, thereby diluting the solution, Q is now less than K. Le Châtelier’s principle tells us that the system will react to relieve the stress—but how? Adding solvent stressed the system by decreasing the concentration of dissolved I2. Hence more crystals will dissolve, thereby increasing the concentration of dissolved I2 until the system again reaches equilibrium if enough solid I2 is available (Figure 14.5.1). By adding solvent, we drove the reaction shown in Equation 14.5.1 to the right as written.
Figure 14.5.1 The Concentration of Dissolved I2 as a Function of Time Following the Addition of More Solvent to a Saturated Solution in Contact with Excess Solid I2 The concentration of I2 decreases initially due to dilution but returns to its original value as long as solid I2 is present.
We encounter a more complex system in the reaction of hydrogen and nitrogen to form ammonia:
\[N_{2(g)}+3H_{2(g)} \rightleftharpoons 2NH_{3(g)} \tag{14.5.2}\]
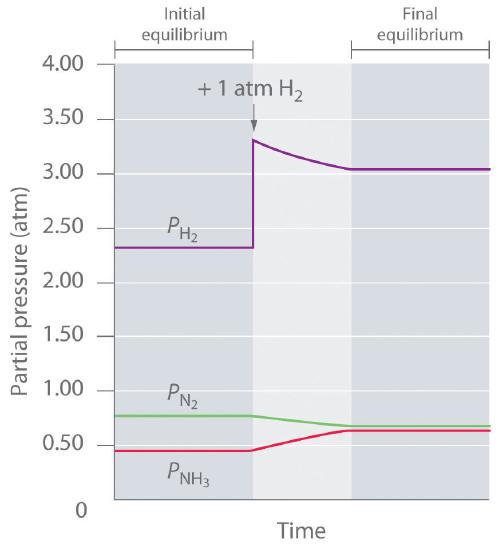
The Kp for this reaction is 2.14 × 10−2 at about 540 K. Under one set of equilibrium conditions, the partial pressure of ammonia is P(NH3) = 0.454 atm, that of hydrogen is P(H2) = 2.319 atm, and that of nitrogen is P(N2) = 0.773 atm. If an additional 1 atm of hydrogen is added to the reactor to give P(H2) = 3.319 atm, how will the system respond? Because the stress is an increase in P(H2) the system must respond in some way that decreases the partial pressure of hydrogen to counteract the stress. The reaction will therefore proceed to the right as written, consuming H2 and N2 and forming additional NH3. Initially, the partial pressures of H2 and N2 will decrease, and the partial pressure of NH3 will increase until the system eventually reaches a new equilibrium composition, which will have a net increase in P(H2)
We can confirm that this is indeed what will happen by evaluating Qp under the new conditions and comparing its value with Kp. The equations used to evaluate Kp and Qp have the same form: substituting the values after adding hydrogen into the expression for Qp results in the following:
\[Q_p=\dfrac{(P_{NH_3})^2}{(P_{N_2})(P_{H_2})^3}=\dfrac{(0.454)^2}{(0.773)(2.319+1.00)^3}=7.29 \times 10^{-3}\]
Thus Qp < Kp, which tells us that the ratio of products to reactants is less than at equilibrium. To reach equilibrium, the reaction must proceed to the right as written: the partial pressures of the products will increase, and the partial pressures of the reactants will decrease. Qp will thereby increase until it equals Kp, and the system will once again be at equilibrium. Changes in the partial pressures of the various substances in the reaction mixture (Equation 14.5.2) as a function of time are shown in Figure 14.5.2.
Figure 14.5.2 The Partial Pressures of H2, N2, and NH3 as a Function of Time Following the Addition of More H2 to an Equilibrium Mixture Some of the added hydrogen is consumed by reacting with nitrogen to produce more ammonia, allowing the system to reach a new equilibrium composition.
We can force a reaction to go essentially to completion, regardless of the magnitude of K, by continually removing one of the products from the reaction mixture. Consider, for example, the methanation reaction, in which hydrogen reacts with carbon monoxide to form methane and water:
\[CO_{(g)}+3H_{2(g)} \rightleftharpoons CH_{4(g)}+H_2O_{(g)} \tag{14.5.3}\]
This reaction is used for the industrial production of methane, whereas the reverse reaction is used for the production of H2 (Example 14). The expression for Q has the following form:
\[Q=\dfrac{[CH_4][H_2O]}{[CO][H_2]^3} \tag{14.5.4}\]
Regardless of the magnitude of K, if either H2O or CH4 can be removed from the reaction mixture so that [H2O] or [CH4] is approximately zero, then Q ≈ 0. In other words, when product is removed, the system is stressed (Q << K), and more product will form to counter the stress. Because water (bp = 100°C) is much less volatile than methane, hydrogen, or carbon monoxide (all of which have boiling points below −100°C), passing the gaseous reaction mixture through a cold coil will cause the water vapor to condense to a liquid that can be drawn off. Continuing to remove water from the system forces the reaction to the right as the system attempts to equilibrate, thus enriching the reaction mixture in methane. This technique, referred to as driving a reaction to completion, can be used to force a reaction to completion even if K is relatively small. For example, esters are usually synthesized by removing water. The products of the condensation reaction are shown here. In Chapter 16, we will describe the thermodynamic basis for the change in the equilibrium position caused by changes in the concentrations of reaction components.
Example 14.5.1
For each equilibrium system, predict the effect of the indicated stress on the specified quantity.
- 2SO2(g) + O2(g) ⇌ 2SO3(g):
(1) the effect of removing O2 on P(SO2)
(2) the effect of removing O2 on P(SO3) - CaCO3(s) ⇌ CaO(s) + CO2(g):
(1) the effect of removing CO2 on the amount of CaCO3;
(2) the effect of adding CaCO3 on P(CO2)
Given: balanced chemical equations and changes
Asked for: effects of indicated stresses
Strategy:
Use Q and K to predict the effect of the stress on each reaction.
Solution:
- (1) Removing O2 will decrease P(O2)thereby decreasing the denominator in the reaction quotient and making Qp > Kp. The reaction will proceed to the left as written, increasing the partial pressures of SO2 and O2 until Qp once again equals Kp.
(2) Removing O2 will decrease P(O2) and thus increase Qp, so the reaction will proceed to the left. The partial pressure of SO3 will decrease. - Kp and Qp are both equal to P(CO2).
(1) Removing CO2 from the system causes more CaCO3 to react to produce CO2, which increases P(CO2) to the partial pressure required by Kp. (2) Adding (or removing) solid CaCO3 has no effect on P(CO2) because it does not appear in the expression for Kp (or Qp).
Exercise
For each equilibrium system, predict the effect that the indicated stress will have on the specified quantity.
- \(H_{2(g)}+CO_{2(g)} \rightleftharpoons H_2O_{(g)}+CO_{(g)}\):
- the effect of adding \(CO\) on \([H_2]\);
- the effect of adding \(CO_2\) on \([H_2]\)
- \(CuO_{(s)}+CO_{(g)} \rightleftharpoons Cu_{(s)}+CO_{2(g)}\):
- the effect of adding \(CO\) on the amount of \(Cu\);
- the effect of adding \(CO_2\) on \([CO]\)
Answer:
- (1) [H2] increases; (2) [H2] decreases.
- (1) the amount of Cu increases; (2) [CO] increases.
Changes in Total Pressure or Volume
Because liquids are relatively incompressible, changing the pressure above a liquid solution has little effect on the concentrations of dissolved substances. Consequently, changes in external pressure have very little effect on equilibrium systems that contain only solids or liquids. In contrast, because gases are highly compressible, their concentrations vary dramatically with pressure. From the ideal gas law, PV = nRT, described in Section 6.3, the concentration (C) of a gas is related to its pressure as follows:
\[C=\dfrac{n}{V}=\dfrac{P}{RT} \tag{14.5.5}\]
Hence the concentration of any gaseous reactant or product is directly proportional to the applied pressure (P) and inversely proportional to the total volume (V). Consequently, the equilibrium compositions of systems that contain gaseous substances are quite sensitive to changes in pressure, volume, and temperature.
These principles can be illustrated using the reversible dissociation of gaseous N2O4 to gaseous NO2 (Equation 14.1.1).
\[N_2O_4 \rightleftharpoons 2 NO_2 \tag{15.1.1} \]
The syringe shown in Figure 14.5.3 initially contains an equilibrium mixture of colorless N2O4 and red-brown NO2. Decreasing the volume by 50% causes the mixture to become darker because all concentrations have doubled. Decreasing the volume also constitutes a stress, however, as we can see by examining the effect of a change in volume on Q. At equilibrium,
\[Q = K = \dfrac{[NO_2]^2}{[N_2O_4]} \tag{14.5.6a}\]
If the volume is decreased by half, the concentrations of the substances in the mixture are doubled, so the new reaction quotient is as follows:
\[Q=\dfrac{(2[NO_2]_i)^2}{2[N_2O_4]_i}=\dfrac{4([NO_2]_i)^2}{2[N_2O_4]_i}=2K \tag{14.5.6b}\]
Because Q is now greater than K, the system is no longer at equilibrium. The stress can be relieved if the reaction proceeds to the left, consuming 2 mol of NO2 for every 1 mol of N2O4 produced. This will decrease the concentration of NO2 and increase the concentration of N2O4, causing Q to decrease until it once again equals K. Thus, as shown in part (c) in Figure 14.5.3, the intensity of the brown color due to NO2 decreases with time following the change in volume.
Figure 14.5.3 The Effect of Changing the Volume (and Thus the Pressure) of an Equilibrium Mixture of N2O4 and NO2 at Constant Temperature (a) The syringe with a total volume of 15 mL contains an equilibrium mixture of N2O4 and NO2; the red-brown color is proportional to the NO2 concentration. (b) If the volume is rapidly decreased by a factor of 2 to 7.5 mL, the initial effect is to double the concentrations of all species present, including NO2. Hence the color becomes more intense. (c) With time, the system adjusts its composition in response to the stress as predicted by Le Châtelier’s principle, forming colorless N2O4 at the expense of red-brown NO2, which decreases the intensity of the color of the mixture. Video from joan-ramon i pinazo
Note the Pattern
Increasing the pressure of a system (or decreasing the volume) favors the side of the reaction that has fewer gaseous molecules and vice versa.
In general, if a balanced chemical equation contains different numbers of gaseous reactant and product molecules, the equilibrium will be sensitive to changes in volume or pressure. Increasing the pressure on a system (or decreasing the volume) will favor the side of the reaction that has fewer gaseous molecules and vice versa.
Example 14.5.2
For each equilibrium system, write the reaction quotient for the system if the pressure is decreased by a factor of 2 (i.e., if the volume is doubled) at constant temperature and then predict the direction of the reaction.
- \(N_{2(g)}+3H_{2(g)} \rightleftharpoons 2NH_{3(g)}\)
- \(C_2H_{2(g)}+C_2H_{6(g)} \rightleftharpoons 2C_2H_{4(g)}\)
- \(2 NO_{2 (g)} \rightleftharpoons 2NO_{(g)}+O_{2(g)}\)
Given: balanced chemical equations
Asked for: direction of reaction if pressure is halved
Strategy:
Use Le Châtelier’s principle to predict the effect of the stress.
Solution:
-
Two moles of gaseous products are formed from 4 mol of gaseous reactants. Decreasing the pressure will cause the reaction to shift to the left because that side contains the larger number of moles of gas. Thus the pressure increases, counteracting the stress. K for this reaction is [NH3]2/[N2][H2]3. When the pressure is decreased by a factor of 2, the concentrations are halved, which means that the new reaction quotient is as follows:
\[Q=\dfrac{[1/2\;NH_3]^2}{[1/2\;N_2][1/2H_2]^3}=\dfrac{1/4\;[NH_3]^2}{1/16\;[N_2][H_2]^3}=4K\]
-
Two moles of gaseous products form from 2 mol of gaseous reactants. Decreasing the pressure will have no effect on the equilibrium composition because both sides of the balanced chemical equation have the same number of moles of gas. Here K = [C2H4]2/[C2H2][C2H6]. The new reaction quotient is as follows:
\[Q=\dfrac{[C_2H_4]^2}{[C_2H_2][C_2H_6]}=\dfrac{[1/2C_2H_4]^2}{[1/2C_2H_2][1/2C_2H_6]}=\dfrac{1/4[C_2H_4]^2}{1/4[C_2H_2][C_2H_6]}=K\]
-
Three moles of gaseous products are formed from 2 mol of gaseous reactants. Decreasing the pressure will favor the side that contains more moles of gas, so the reaction will shift toward the products to increase the pressure. For this reaction K = [NO]2[O2]/[NO2]2. Under the new reaction conditions the reaction quotient is as follows:
\[Q=\dfrac{[1/2NO]^2[1/2O_2]}{[1/2 NO_2]^2}=\dfrac{1/8[NO]^2[O_2]}{1/4[NO_2]^2}=1/2K\]
Exercise
For each equilibrium system, write a new reaction quotient for the system if the pressure is increased by a factor of 2 (i.e., if the volume is halved) at constant temperature and then predict the direction in which the reaction will shift.
- \(H_2O_{(g)}+CO_{(g)} \rightleftharpoons H_{2(g)}+CO_{2(g)}\)
- \(H_{2(g)}+C_2H_{4(g)} \rightleftharpoons C_2H_{6(g)}\)
- \(2SO_{2(g)}+O_{2(g)} \rightleftharpoons 2SO_{3(g)}\)
Answer:
- Q = K; no effect
- Q = 1/2 K; to the right
- Q = 1/2 K; to the right
Changes in Temperature
In all the cases we have considered so far, the magnitude of the equilibrium constant, K or Kp, was constant. Changes in temperature can, however, change the value of the equilibrium constant without immediately affecting the reaction quotient (Q ≠ K). In this case, the system is no longer at equilibrium; the composition of the system will change until Q equals K at the new temperature.
To predict how an equilibrium system will respond to a change in temperature, we must know something about the enthalpy change of the reaction (ΔHrxn). As you will learn in the next chapter, Chapter 15, heat is released to the surroundings in an exothermic reaction (ΔHrxn < 0), and heat is absorbed from the surroundings in an endothermic reaction (ΔHrxn > 0). We can express these changes in the following way:
- Exothermic (ΔH<0): \[\text{reactants} \rightleftharpoons \text{products} + \text{heat} \tag{14.5.7}\]
- Endothermic (ΔH>0): \[\text{reactants} + \text{heat} \rightleftharpoons \text{products} \tag{14.5.8}\]
Thus heat can be thought of as a product in an exothermic reaction and as a reactant in an endothermic reaction. Increasing the temperature of a system corresponds to adding heat. Le Châtelier’s principle predicts that an exothermic reaction will shift to the left (toward the reactants) if the temperature of the system is increased (heat is added). Conversely, an endothermic reaction will shift to the right (toward the products) if the temperature of the system is increased. If a reaction is thermochemically neutral (ΔHrxn = 0), then a change in temperature will not affect the equilibrium composition.
We can examine the effects of temperature on the dissociation of N2O4 to NO2, for which ΔH = +58 kJ/mol. This reaction can be written as follows:
\[58\; kJ+N_2O_{4(g)} \rightleftharpoons 2 NO_{2(g)} \tag{14.5.9}\]
Increasing the temperature (adding heat to the system) is a stress that will drive the reaction to the right, as illustrated in Figure 14.5.4. Thus increasing the temperature increases the ratio of NO2 to N2O4 at equilibrium, which increases K.
Figure 14.5.4 The Effect of Temperature on the Equilibrium between Gaseous N2O4 and NO2 The value of \(K\) changes with temperature of the same 99.9% pure \(NO_2/N_2O_4\) sealed in an ampoule. From left to right -196° C, 0° C, 23° C, 35° C, 50° C. In the endothermic reaction , the equilibrium position can be shifted by changing the temperature. When heat is added and the temperature increases, the reaction shifts to the right and the flask turns reddish brown due to an increase in \(NO_2\). When heat is removed and the temperature decreases, the reaction shifts to the left and flask turns colorless due to an increase in \(N_2O_4\). This demonstrates Le Chatelier’s Principle because the equilibrium shifts in the direction that consumes energy. Figure used with permission from Wikipedia.
The effect of increasing the temperature on a system at equilibrium can be summarized as follows: increasing the temperature increases the magnitude of the equilibrium constant for an endothermic reaction, decreases the equilibrium constant for an exothermic reaction, and has no effect on the equilibrium constant for a thermally neutral reaction. Table 14.5.1 shows the temperature dependence of the equilibrium constants for the synthesis of ammonia from hydrogen and nitrogen, which is an exothermic reaction with ΔH° = −91.8 kJ/mol. The values of both K and Kp decrease dramatically with increasing temperature, as predicted for an exothermic reaction.
Table 14.5.1 Temperature Dependence of K and Kp for N2(g) + 3 H2 (g) ⇌ 2 NH3(g)
| Temperature (K) | K | K p |
|---|---|---|
| 298 | 3.3 × 108 | 5.6 × 105 |
| 400 | 3.9 × 104 | 3.6 × 101 |
| 450 | 2.6 × 103 | 1.9 |
| 500 | 1.7 × 102 | 1.0 × 10−1 |
| 550 | 2.6 × 101 | 1.3 × 10−2 |
| 600 | 4.1 | 1.7 × 10−3 |
Note the Pattern
Increasing the temperature causes endothermic reactions to favor products and exothermic reactions to favor reactants.
Example 14.5.3
For each equilibrium reaction, predict the effect of decreasing the temperature:
- \(N_{2(g)}+3H_{2(g)} \rightleftharpoons 2NH_{3(g)}\;\;\; ΔH_{rxn}=−91.8\; kJ/mol\)
- \(CaCO_{3(s)} \rightleftharpoons CaO_{(s)}+CO_{2(g)}\;\;\; ΔH_{rxn}=178\; kJ/mol\)
Given: balanced chemical equations and values of ΔHrxn
Asked for: effects of decreasing temperature
Strategy:
Use Le Châtelier’s principle to predict the effect of decreasing the temperature on each reaction.
Solution:
-
The formation of NH3 is exothermic, so we can view heat as one of the products:
\[N_{2(g)}+3H_{2(g)} \rightleftharpoons 2NH_{3(g)}+91.8\; kJ\]
-
If the temperature of the mixture is decreased, heat (one of the products) is being removed from the system, which causes the equilibrium to shift to the right. Hence the formation of ammonia is favored at lower temperatures.
-
The decomposition of calcium carbonate is endothermic, so heat can be viewed as one of the reactants:
\[CaCO_{3(s)}+178 \;kJ \rightleftharpoons CaO_{(s)}+CO_{2(g)}\]If the temperature of the mixture is decreased, heat (one of the reactants) is being removed from the system, which causes the equilibrium to shift to the left. Hence the thermal decomposition of calcium carbonate is less favored at lower temperatures.
Exercise
For each equilibrium system, predict the effect of increasing the temperature on the reaction mixture:
- \(2SO_{2(g)}+O_{2(g)} \rightleftharpoons 2SO_{3(g)}\) with \(ΔH_{rxn}=−198\; kJ/mol\)
- \(N_{2(g)}+O_{2(g)} \rightleftharpoons 2NO_{(g)}\) with \(ΔH_{rxn}=+181\; kJ/mol\)
Answer:
- Reaction shifts to the left.
- Reaction shifts to the right.
Summary
Three types of stresses can alter the composition of an equilibrium system: adding or removing reactants or products, changing the total pressure or volume, and changing the temperature of the system. A reaction with an unfavorable equilibrium constant can be driven to completion by continually removing one of the products of the reaction. Equilibriums that contain different numbers of gaseous reactant and product molecules are sensitive to changes in volume or pressure; higher pressures favor the side with fewer gaseous molecules. Removing heat from an exothermic reaction favors the formation of products, whereas removing heat from an endothermic reaction favors the formation of reactants.
Key Takeaway
- Equilibriums are affected by changes in concentration, total pressure or volume, and temperature.
Conceptual Problems
-
If an equilibrium reaction is endothermic in the forward direction, what is the expected change in the concentration of each component of the system if the temperature of the reaction is increased? If the temperature is decreased?
-
Write the equilibrium equation for the following system:
\[4NH_{3(g)} +5O_{2(g)} \rightleftharpoons 4NO_{(g)} + 6H_2O_{(g)}\
Would you expect the equilibrium to shift toward the products or reactants with an increase in pressure? Why?
-
The reaction rate approximately doubles for every 10°C rise in temperature. What happens to K?
-
The formation of A2B2(g) via the equilibrium reaction 2AB(g) ⇌ A2B2(g) is exothermic. What happens to the ratio kf/kr if the temperature is increased? If both temperature and pressure are increased?
-
In each system, predict the effect that the indicated change will have on the specified quantity at equilibrium:
-
\(H_{2(g)}+I_{2(g)} \rightleftharpoons 2HI_{(g)}\):
H2 is removed; what is the effect on P(I2)?
-
\(2NOBr_{(g)} \rightleftharpoons 2NO_{(g)} + Br_{2(g)}\)
If Br2 is removed; what is the effect on PNOBr?
-
\(2NaHCO_{3(s)} \rightleftharpoons Na_2CO_{3(g)} + CO_{2(g)}+H_2O_{(g)}\)
If CO2 is removed; what is the effect on P(NaHCO3)?
-
-
What effect will the indicated change have on the specified quantity at equilibrium?
-
\(NH_4Cl_{(s)} \rightleftharpoons NH_{3(g)}+HCl_{(g)}\)
If NH4Cl is increased; what is the effect on PHCl?
-
\(2H2O_{(g)} \rightleftharpoons 2H_{2(g)}+O_{2(g)}\)
If O2 is added; what is the effect on P(H2)?<
-
\(PCl_{3(g)}+Cl_{2(g)} \rightleftharpoons PCl_{5(g)}\)
If Cl2 is removed; what is the effect on P(PCl5)?
-
Numerical Problems
-
For each equilibrium reaction, describe how Q and K change when the pressure is increased, the temperature is increased, the volume of the system is increased, and the concentration(s) of the reactant(s) is increased.
- A(g) ⇌ B(g) Δ H = −20.6 kJ/mol
- 2A(g) ⇌ B(g) Δ H = −0.3 kJ/mol
- A(g) + B(g) ⇌ 2C(g) Δ H = 46 kJ/mol
-
For each equilibrium reaction, describe how Q and K change when the pressure is decreased, the temperature is increased, the volume of the system is decreased, and the concentration(s) of the reactant(s) is increased.
- 2A(g) ⇌ B(g) Δ H = −80 kJ/mol
- A(g) ⇌ 2B(g) Δ H = 0.3 kJ/mol
- 2A(g) ⇌ 2B(g) + C(g) Δ H = 46 kJ/mol
-
Le Châtelier’s principle states that a system will change its composition to counteract stress. For the system CO(g) + Cl2(g) ⇌ COCl2(g), write the equilibrium constant expression Kp. What changes in the values of Q and K would you anticipate when (a) the volume is doubled, (b) the pressure is increased by a factor of 2, and (c) COCl2 is removed from the system?
-
For the equilibrium system 3O2(g) ⇌ 2 O3(g), ΔH° = 284 kJ, write the equilibrium constant expression Kp. What happens to the values of Q and K if the reaction temperature is increased? What happens to these values if both the temperature and pressure are increased?
-
Carbon and oxygen react to form CO2 gas via C(s) + O2(g) ⇌ CO2(g), for which K = 1.2 × 1069. Would you expect K to increase or decrease if the volume of the system were tripled? Why?
-
The reaction COCl2(g) ⇌ CO(g) + Cl2 (g) has K = 2.2 × 10−10 at 100°C. Starting with an initial P( COCl2) of 1.0 atm, you determine the following values of PCO at three successive time intervals: 6.32 × 10−6 atm, 1.78 × 10−6 atm, and 1.02 × 10−5 atm. Based on these data, in which direction will the reaction proceed after each measurement? If chlorine gas is added to the system, what will be the effect on Q?
-
The following table lists experimentally determined partial pressures at three temperatures for the reaction Br2(g) ⇌ 2 Br(g)
T (K) 1123 1173 1273 P(Br2) (atm) 3.000 0.3333 6.755 × 10−2 P(Br) (atm) 3.477 × 10−2 2.159 × 10−2 2.191 × 10−2 Is this an endothermic or an exothermic reaction? Explain your reasoning.
-
The dissociation of water vapor proceeds according to the following reaction:H2O(g) ⇌ 1/2 O2(g) + H2 (g). At 1300 K, there is 0.0027% dissociation, whereas at 2155 K, the dissociation is 1.18%. Calculate K and Kp. Is this an endothermic reaction or an exothermic reaction? How do the magnitudes of the two equilibriums compare? Would increasing the pressure improve the yield of H2 gas at either temperature? (Hint: assume that the system initially contains 1.00 mol of H2O in a 1.00 L container.)
-
When 1.33 mol of CO2 and 1.33 mol of H2 are mixed in a 0.750 L container and heated to 395°C, they react according to the following equation: CO2(g) + H2 (g) ⇌ CO(g) + H2O(g) If K = 0.802, what are the equilibrium concentrations of each component of the equilibrium mixture? What happens to K if H2O is removed during the course of the reaction?
-
The equilibrium reaction H2(g) + Br2(g) ⇌ 2 HBr(g) has Kp = 2.2 × 109 at 298 K. If you begin with 2.0 mol of Br2 and 2.0 mol of H2 in a 5.0 L container, what is the partial pressure of HBr at equilibrium? What is the partial pressure of H2 at equilibrium? If H2 is removed from the system, what is the effect on the partial pressure of Br2?
-
Iron(II) oxide reacts with carbon monoxide according to the following equation: FeO(s) + CO(g) ⇌ Fe(s) + CO2(g) At 800°C, K = 0.34; at 1000°C, K = 0.40.
- A 20.0 L container is charged with 800.0 g of CO2, 1436 g of FeO, and 1120 g of iron. What are the equilibrium concentrations of all components of the mixture at each temperature?
- What are the partial pressures of the gases at each temperature?
- If CO were removed, what would be the effect on P(CO2) at each temperature?
-
The equilibrium constant K for the reaction C(s) + CO2 g) >⇌ 2 CO(g) is 1.9 at 1000 K and 0.133 at 298 K.
- If excess C is allowed to react with 25.0 g of CO2 in a 3.00 L flask, how many grams of CO are produced at each temperature?
- What are the partial pressures of each gas at 298 K? at 1000 K?
- Would you expect K to increase or decrease if the pressure were increased at constant temperature and volume?
-
Data for the oxidation of methane, CH4(g) + 2 O2(g) ⇌ CO2(g) + 2 H2O(g), in a closed 5.0 L vessel are listed in the following table. Fill in the blanks and determine the missing values of Q and K (indicated by ?) as the reaction is driven to completion.
CH4 O2 CO2 H2O Q K initial (moles) 0.45 0.90 0 0 ? at equilibrium 1.29 add 0.50 mol of methane 0.95 ? new equilibrium ? remove water 0 ? new equilibrium 1.29
Answers
-
Kp = P(COCl2)/(P(CO) P(Cl2)) PNone of the changes would affect K; (a) Q doubles; (b) Q is halved; Q decreases.
-
K would not change; it does not depend on volume.
-
[CO] = [H2O] = 0.839 M, [CO2] = [H2] = 0.930 M; no effect on K
-
- At 800°C, [CO] = 0.678 M, [CO2] = 0.231 M; at 1000°C, [CO] = 0.645 M, [CO2] = 0.264 M
- At 800°C, PCO = 59.7 atm, P(CO2) = 20.3 atm; at 1000°C, P(CO) = 67.4 atm, P(CO2) = 27.6 atm.
- Removing CO would cause the reaction to shift to the right, causing P(CO2) to decrease.
-
CH4 O2 CO2 H2O Q K initial (moles) 0.45 0.90 0 0 0 1.29 at equilibrium 0.215 0.43 0.235 0.47 K 1.29 add 0.50 mol of methane 0.715 0.43 0.235 0.47 0.39 1.29 new equilibrium 0.665 0.33 0.285 0.57 K 1.29 remove water 0.665 0.33 0.285 0 0 1.29 new equilibrium 0.57 0.14 0.38 0.19 K 1.29
Contributors
- Anonymous
Modified by Joshua Halpern (Howard University), Scott Sinex, and Scott Johnson (PGCC)
Video from joan-ramon i pinazo on YouTube