3.8: Electrolysis

Learning Objectives

• To understand electrolysis and describe it quantitatively.

In this chapter, we have described various galvanic cells in which a spontaneous chemical reaction is used to generate electrical energy. In an electrolytic cell, however, the opposite process, called electrolysis, occurs: an external voltage is applied to drive a nonspontaneous reaction. In this section, we look at how electrolytic cells are constructed and explore some of their many commercial applications.

Electrolytic Cells

If we construct an electrochemical cell in which one electrode is copper metal immersed in a 1 M Cu²⁺ solution and the other electrode is cadmium metal immersed in a \(\,1\; M\, Cd^{2+}\) solution and then close the circuit, the potential difference between the two compartments will be 0.74 V. The cadmium electrode will begin to dissolve (Cd is oxidized to Cd²⁺) and is the anode, while metallic copper will be deposited on the copper electrode (Cu²⁺ is reduced to Cu), which is the cathode (Figure \(\PageIndex{1a}\)).

Figure \(\PageIndex{1}\): An Applied Voltage Can Reverse the Flow of Electrons in a Galvanic Cd/Cu Cell. (a) When compartments that contain a Cd electrode immersed in 1 M Cd²⁺(aq) and a Cu electrode immersed in 1 M Cu²⁺(aq) are connected to create a galvanic cell, Cd(s) is spontaneously oxidized to Cd²⁺(aq) at the anode, and Cu²⁺(aq) is spontaneously reduced to Cu(s) at the cathode. The potential of the galvanic cell is 0.74 V. (b) Applying an external potential greater than 0.74 V in the reverse direction forces electrons to flow from the Cu electrode [which is now the anode, at which metallic Cu(s) is oxidized to Cu²⁺(aq)] and into the Cd electrode [which is now the cathode, at which Cd²⁺(aq) is reduced to Cd(s)]. The anode in an electrolytic cell is positive because electrons are flowing from it, whereas the cathode is negative because electrons are flowing into it.

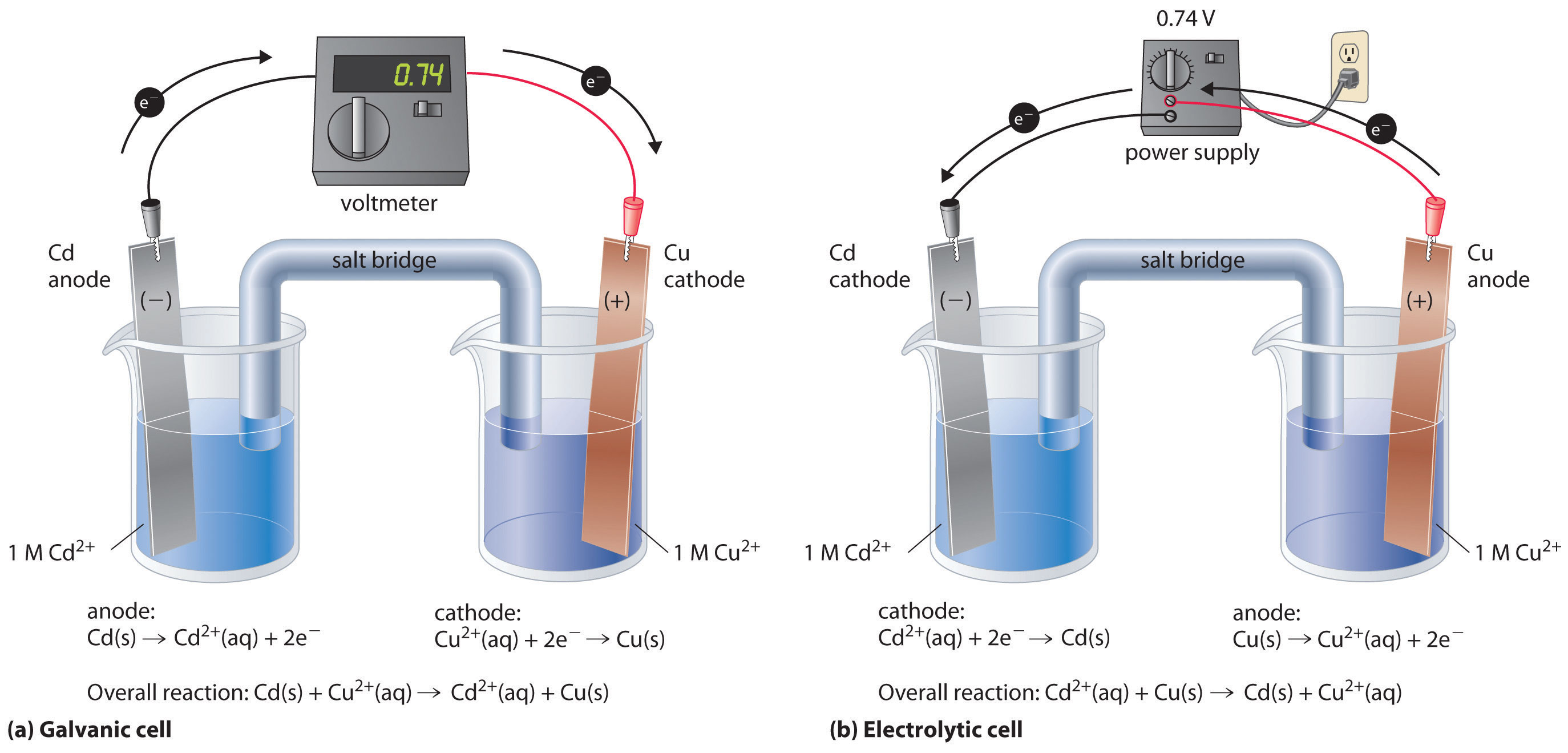
The overall reaction is as follows:

\[ \ce{Cd (s) + Cu^{2+} (aq) \rightarrow Cd^{2+} (aq) + Cu (s)} \label{20.9.1}\]

with \(E°_{cell} = 0.74\; V\)

This reaction is thermodynamically spontaneous as written (ΔG° < 0):

\[ \begin{align} \Delta G^\circ &=-nFE^\circ_\textrm{cell} \label{20.9.2a} \\[4pt] &=-(\textrm{2 mol e}^-)[\mathrm{96,486\;J/(V\cdot mol)}](\mathrm{0.74\;V}) \\[4pt] &=-\textrm{140 kJ (per mole Cd)} \label{20.9.2b} \end{align}\]

In this direction, the system is acting as a galvanic cell.

In an electrolytic cell, an external voltage is applied to drive a nonspontaneous reaction.

The reverse reaction, the reduction of Cd²⁺ by Cu, is thermodynamically nonspontaneous and will occur only with an input of 140 kJ. We can force the reaction to proceed in the reverse direction by applying an electrical potential greater than 0.74 V from an external power supply. The applied voltage forces electrons through the circuit in the reverse direction, converting a galvanic cell to an electrolytic cell. Thus the copper electrode is now the anode (Cu is oxidized), and the cadmium electrode is now the cathode (Cd²⁺ is reduced) (Figure \(\PageIndex{1b}\)). The signs of the cathode and the anode have switched to reflect the flow of electrons in the circuit. The half-reactions that occur at the cathode and the anode are as follows:

• cathode:

\[\ce{Cd^{2+}(aq) + 2e^{−} \rightarrow Cd(s)}\label{20.9.3}\]

with \(E^°_{cathode} = −0.40 \, V\)

• anode:

\[\ce{Cu(s) \rightarrow Cu^{2+}(aq) + 2e^{−}} \label{20.9.4}\]

with \(E^°_{anode} = 0.34 \, V \)

• Overall:

\[\ce{Cd^{2+}(aq) + Cu(s) \rightarrow Cd(s) + Cu^{2+}(aq) } \label{20.9.5}\]

with \(E^°_{cell} = −0.74 \: V\)

Because \( E^°_{cell} < 0\), the overall reaction—the reduction of \(Cd^{2+}\) by \(Cu\)—clearly cannot occur spontaneously and proceeds only when sufficient electrical energy is applied. The differences between galvanic and electrolytic cells are summarized in Table \(\PageIndex{1}\).

Table \(\PageIndex{1}\): Comparison of Galvanic and Electrolytic Cells

Property	Galvanic Cell	Electrolytic Cell
ΔG	< 0	> 0
Ecell	> 0	< 0
Electrode Process
anode	oxidation	oxidation
cathode	reduction	reduction
Sign of Electrode
anode	−	+
cathode	+	−

Electrolytic Reactions

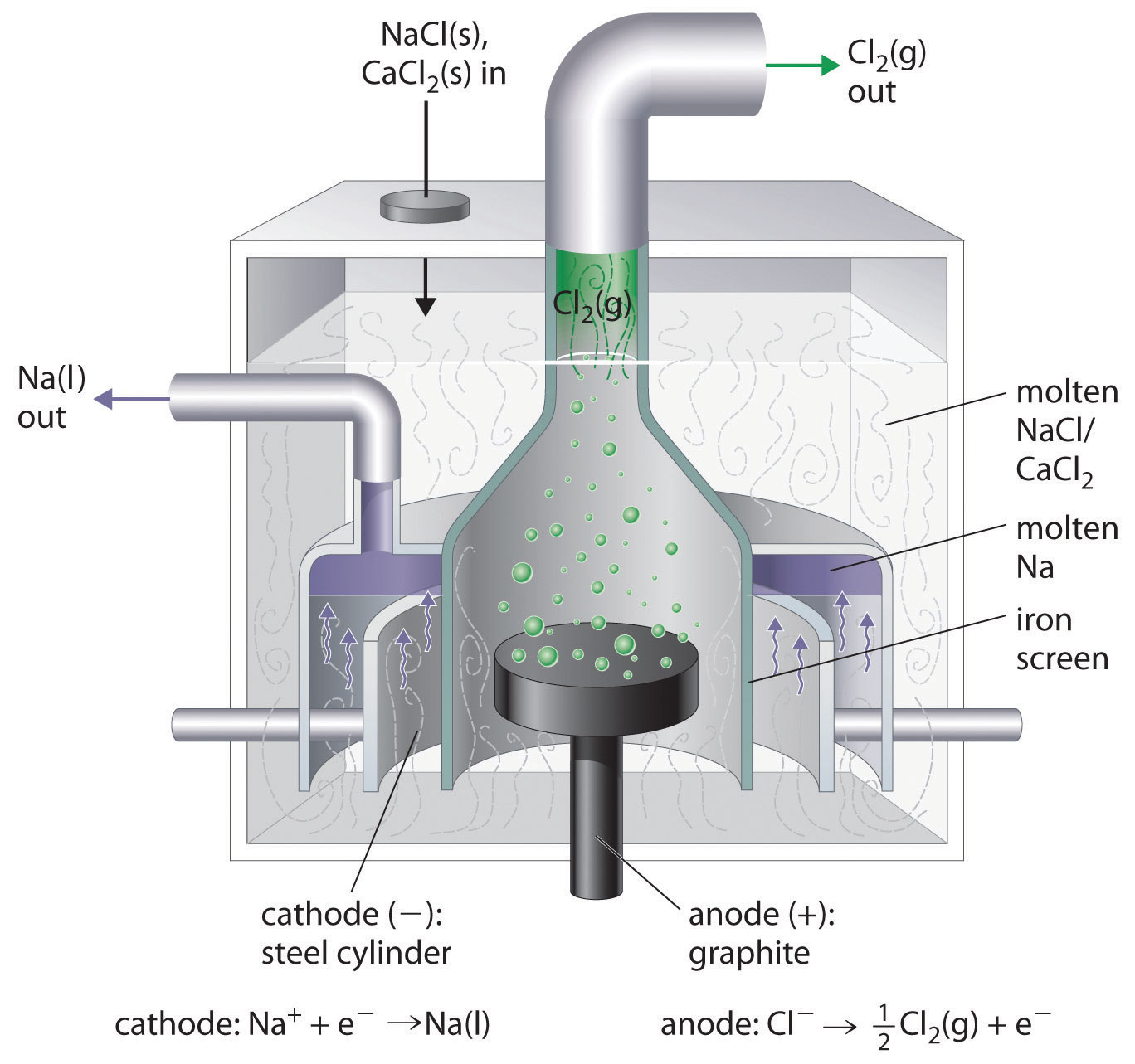
At sufficiently high temperatures, ionic solids melt to form liquids that conduct electricity extremely well due to the high concentrations of ions. If two inert electrodes are inserted into molten \(NaCl\), for example, and an electrical potential is applied, \(Cl^−\) is oxidized at the anode, and \(Na^+\) is reduced at the cathode. The overall reaction is as follows:

\[\ce{ 2NaCl (l) \rightarrow 2Na(l) + Cl2(g)} \label{20.9.6}\]

This is the reverse of the formation of NaCl from its elements. The product of the reduction reaction is liquid sodium because the melting point of sodium metal is 97.8°C, well below that of \(NaCl\) (801°C). Approximately 20,000 tons of sodium metal are produced commercially in the United States each year by the electrolysis of molten \(NaCl\) in a Downs cell (Figure \(\PageIndex{2}\)). In this specialized cell, \(CaCl_2\) (melting point = 772°C) is first added to the \(NaCl\) to lower the melting point of the mixture to about 600°C, thereby lowering operating costs.

Figure \(\PageIndex{2}\): A Downs Cell for the Electrolysis of Molten NaCl. The electrolysis of a molten mixture of NaCl and CaCl₂ results in the formation of elemental sodium and chlorine gas. Because sodium is a liquid under these conditions and liquid sodium is less dense than molten sodium chloride, the sodium floats to the top of the melt and is collected in concentric capped iron cylinders surrounding the cathode. Gaseous chlorine collects in the inverted cone over the anode. An iron screen separating the cathode and anode compartments ensures that the molten sodium and gaseous chlorine do not come into contact.

Similarly, in the Hall–Heroult process used to produce aluminum commercially, a molten mixture of about 5% aluminum oxide (Al₂O₃; melting point = 2054°C) and 95% cryolite (Na₃AlF₆; melting point = 1012°C) is electrolyzed at about 1000°C, producing molten aluminum at the cathode and CO₂ gas at the carbon anode. The overall reaction is as follows:

\[2Al_2O_{3(l)} + 3C_{(s)} \rightarrow 4Al_{(l)} + 3CO_{2(g)} \label{20.9.7}\]

Oxide ions react with oxidized carbon at the anode, producing CO₂(g).

There are two important points to make about these two commercial processes and about the electrolysis of molten salts in general.

1. The electrode potentials for molten salts are likely to be very different from the standard cell potentials listed in Table P2, which are compiled for the reduction of the hydrated ions in aqueous solutions under standard conditions.
2. Using a mixed salt system means there is a possibility of competition between different electrolytic reactions. When a mixture of NaCl and CaCl₂ is electrolyzed, Cl⁻ is oxidized because it is the only anion present, but either Na⁺ or Ca²⁺ can be reduced. Conversely, in the Hall–Heroult process, only one cation is present that can be reduced (Al³⁺), but there are three species that can be oxidized: C, O²⁻, and F⁻.

In the Hall–Heroult process, C is oxidized instead of O²⁻ or F⁻ because oxygen and fluorine are more electronegative than carbon, which means that C is a weaker oxidant than either O₂ or F₂. Similarly, in the Downs cell, we might expect electrolysis of a NaCl/CaCl₂ mixture to produce calcium rather than sodium because Na is slightly less electronegative than Ca (χ = 0.93 versus 1.00, respectively), making Na easier to oxidize and, conversely, Na⁺ more difficult to reduce. In fact, the reduction of Na⁺ to Na is the observed reaction. In cases where the electronegativities of two species are similar, other factors, such as the formation of complex ions, become important and may determine the outcome.

Example \(\PageIndex{1}\)

If a molten mixture of MgCl₂ and KBr is electrolyzed, what products will form at the cathode and the anode, respectively?

Given: identity of salts

Asked for: electrolysis products

Strategy:

1. List all the possible reduction and oxidation products. Based on the electronegativity values shown in Figure 7.5, determine which species will be reduced and which species will be oxidized.
2. Identify the products that will form at each electrode.

Solution

A The possible reduction products are Mg and K, and the possible oxidation products are Cl₂ and Br₂. Because Mg is more electronegative than K (χ = 1.31 versus 0.82), it is likely that Mg will be reduced rather than K. Because Cl is more electronegative than Br (3.16 versus 2.96), Cl₂ is a stronger oxidant than Br₂.

B Electrolysis will therefore produce Br₂ at the anode and Mg at the cathode.

Exercise \(\PageIndex{1}\)

Predict the products if a molten mixture of AlBr₃ and LiF is electrolyzed.

Answer

Br₂ and Al

Electrolysis can also be used to drive the thermodynamically nonspontaneous decomposition of water into its constituent elements: H₂ and O₂. However, because pure water is a very poor electrical conductor, a small amount of an ionic solute (such as H₂SO₄ or Na₂SO₄) must first be added to increase its electrical conductivity. Inserting inert electrodes into the solution and applying a voltage between them will result in the rapid evolution of bubbles of H₂ and O₂ (Figure \(\PageIndex{3}\)).

Figure \(\PageIndex{3}\): The Electrolysis of Water. Applying an external potential of about 1.7–1.9 V to two inert electrodes immersed in an aqueous solution of an electrolyte such as H₂SO₄ or Na₂SO₄ drives the thermodynamically nonspontaneous decomposition of water into H₂ at the cathode and O₂ at the anode.

The reactions that occur are as follows:

• cathode: \[2H^+_{(aq)} + 2e^− \rightarrow H_{2(g)} \;\;\; E^°_{cathode} = 0 V \label{20.9.8}\]
• anode: \[2H_2O_{(l)} → O_{2(g)} + 4H+_{(aq)} + 4e^−\;\;\; E^°_{anode} = 1.23\; V \label{20.9.9}\]
• overall: \[2H_2O_{(l)} → O_{2(g)} + 2H_{2(g)}\;\;\; E^°_{cell} = −1.23 \;V \label{20.9.10}\]

For a system that contains an electrolyte such as Na₂SO₄, which has a negligible effect on the ionization equilibrium of liquid water, the pH of the solution will be 7.00 and [H⁺] = [OH⁻] = 1.0 × 10⁻⁷. Assuming that \(P_\mathrm{O_2}\) = \(P_\mathrm{H_2}\) = 1 atm, we can use the standard potentials to calculate E for the overall reaction:

\[\begin{align}E_\textrm{cell} &=E^\circ_\textrm{cell}-\left(\dfrac{\textrm{0.0591 V}}{n}\right)\log(P_\mathrm{O_2}P^2_\mathrm{H_2}) \\ E_\textrm{cell} &=-\textrm{1.23 V}-\left(\dfrac{\textrm{0.0591 V}}{4}\right)\log(1)=-\textrm{1.23 V}\end{align} \label{20.9.11}\]

Thus E_cell is −1.23 V, which is the value of E°_cell if the reaction is carried out in the presence of 1 M H⁺ rather than at pH 7.0.

In practice, a voltage about 0.4–0.6 V greater than the calculated value is needed to electrolyze water. This added voltage, called an overvoltage, represents the additional driving force required to overcome barriers such as the large activation energy for the formation of a gas at a metal surface. Overvoltages are needed in all electrolytic processes, which explain why, for example, approximately 14 V must be applied to recharge the 12 V battery in your car.

In general, any metal that does not react readily with water to produce hydrogen can be produced by the electrolytic reduction of an aqueous solution that contains the metal cation. The p-block metals and most of the transition metals are in this category, but metals in high oxidation states, which form oxoanions, cannot be reduced to the metal by simple electrolysis. Active metals, such as aluminum and those of groups 1 and 2, react so readily with water that they can be prepared only by the electrolysis of molten salts. Similarly, any nonmetallic element that does not readily oxidize water to O₂ can be prepared by the electrolytic oxidation of an aqueous solution that contains an appropriate anion. In practice, among the nonmetals, only F₂ cannot be prepared using this method. Oxoanions of nonmetals in their highest oxidation states, such as NO₃⁻, SO₄²⁻, PO₄³⁻, are usually difficult to reduce electrochemically and usually behave like spectator ions that remain in solution during electrolysis.

In general, any metal that does not react readily with water to produce hydrogen can be produced by the electrolytic reduction of an aqueous solution that contains the metal cation.

Electroplating

In a process called electroplating, a layer of a second metal is deposited on the metal electrode that acts as the cathode during electrolysis. Electroplating is used to enhance the appearance of metal objects and protect them from corrosion. Examples of electroplating include the chromium layer found on many bathroom fixtures or (in earlier days) on the bumpers and hubcaps of cars, as well as the thin layer of precious metal that coats silver-plated dinnerware or jewelry. In all cases, the basic concept is the same. A schematic view of an apparatus for electroplating silverware and a photograph of a commercial electroplating cell are shown in Figure \(\PageIndex{4}\).

Figure \(\PageIndex{3}\): Electroplating. (a) Electroplating uses an electrolytic cell in which the object to be plated, such as a fork, is immersed in a solution of the metal to be deposited. The object being plated acts as the cathode, on which the desired metal is deposited in a thin layer, while the anode usually consists of the metal that is being deposited (in this case, silver) that maintains the solution concentration as it dissolves. (b) In this commercial electroplating apparatus, a large number of objects can be plated simultaneously by lowering the rack into the Ag+ solution and applying the correct potential.

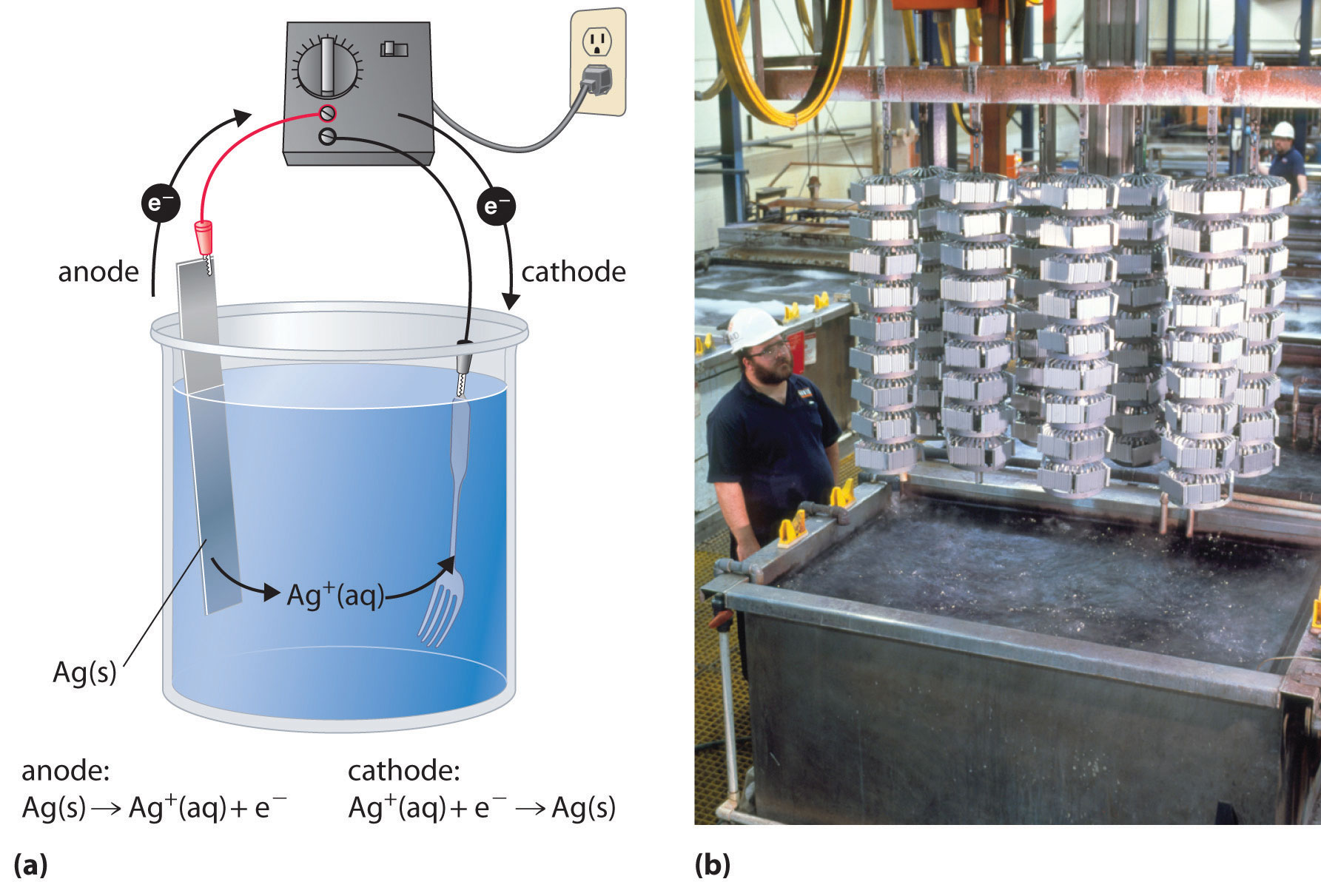
The half-reactions in electroplating a fork, for example, with silver are as follows:

• cathode (fork): \[Ag^+_{(aq)} + e− \rightarrow Ag_{(s)}\;\;\; E°_{cathode} = 0.80 V\label{20.9.12}\]
• anode (silver bar): \[Ag_{(s)} \rightarrow Ag^+_{(aq)}\;\;\; E°_{anode} = 0.80 V \label{20.9.13}\]

The overall reaction is the transfer of silver metal from one electrode (a silver bar acting as the anode) to another (a fork acting as the cathode). Because E°_cell = 0 V, it takes only a small applied voltage to drive the electroplating process. In practice, various other substances may be added to the plating solution to control its electrical conductivity and regulate the concentration of free metal ions, thus ensuring a smooth, even coating.

Quantitative Considerations

If we know the stoichiometry of an electrolysis reaction, the amount of current passed, and the length of time, we can calculate the amount of material consumed or produced in a reaction. Conversely, we can use stoichiometry to determine the combination of current and time needed to produce a given amount of material.

The quantity of material that is oxidized or reduced at an electrode during an electrochemical reaction is determined by the stoichiometry of the reaction and the amount of charge that is transferred. For example, in the reaction Ag⁺(aq) + e⁻ → Ag(s), 1 mol of electrons reduces 1 mol of Ag⁺ to Ag metal. In contrast, in the reaction Cu²⁺(aq) + 2e⁻ → Cu(s), 1 mol of electrons reduces only 0.5 mol of Cu²⁺ to Cu metal. Recall that the charge on 1 mol of electrons is 1 faraday (1 F), which is equal to 96,486 C. We can therefore calculate the number of moles of electrons transferred when a known current is passed through a cell for a given period of time. The total charge (C) transferred is the product of the current (A) and the time (t, in seconds):

\[ C = A \times t \label{20.9.14}\]

The stoichiometry of the reaction and the total charge transferred enable us to calculate the amount of product formed during an electrolysis reaction or the amount of metal deposited in an electroplating process.

For example, if a current of 0.60 A passes through an aqueous solution of CuSO₄ for 6.0 min, the total number of coulombs of charge that passes through the cell is as follows:

\(\textrm{charge}=\textrm{(0.60 A)(6.0 min)(60 s/min)}=\mathrm{220\;A\cdot s}=\textrm{220 C} \label{20.9.15}\)

The number of moles of electrons transferred to \(Cu^{2+}\) is therefore

\(\textrm{moles e}^-=\dfrac{\textrm{220 C}}{\textrm{96,486 C/mol}}=2.3\times10^{-3}\textrm{ mol e}^- \label{20.9.16}\)

Because two electrons are required to reduce a single Cu²⁺ ion, the total number of moles of Cu produced is half the number of moles of electrons transferred, or 1.2 × 10⁻³ mol. This corresponds to 76 mg of Cu. In commercial electrorefining processes, much higher currents (greater than or equal to 50,000 A) are used, corresponding to approximately 0.5 F/s, and reaction times are on the order of 3–4 weeks.

Example \(\PageIndex{2}\)

A silver-plated spoon typically contains about 2.00 g of Ag. If 12.0 h are required to achieve the desired thickness of the Ag coating, what is the average current per spoon that must flow during the electroplating process, assuming an efficiency of 100%?

Given: mass of metal, time, and efficiency

Asked for: current required

Strategy:

1. Calculate the number of moles of metal corresponding to the given mass transferred.
2. Write the reaction and determine the number of moles of electrons required for the electroplating process.
3. Use the definition of the faraday to calculate the number of coulombs required. Then convert coulombs to current in amperes.

Solution

A We must first determine the number of moles of Ag corresponding to 2.00 g of Ag:

\(\textrm{moles Ag}=\dfrac{\textrm{2.00 g}}{\textrm{107.868 g/mol}}=1.85\times10^{-2}\textrm{ mol Ag}\)

B The reduction reaction is Ag⁺(aq) + e⁻ → Ag(s), so 1 mol of electrons produces 1 mol of silver.

C Using the definition of the faraday,

coulombs = (1.85 × 10⁻²mol e⁻)(96,486 C/mol e⁻) = 1.78 × 10³ C / mole

The current in amperes needed to deliver this amount of charge in 12.0 h is therefore

\(\begin{align}\textrm{amperes} &=\dfrac{1.78\times10^3\textrm{ C}}{(\textrm{12.0 h})(\textrm{60 min/h})(\textrm{60 s/min})}\\
& =4.12\times10^{-2}\textrm{ C/s}=4.12\times10^{-2}\textrm{ A}\end{align}\)

Because the electroplating process is usually much less than 100% efficient (typical values are closer to 30%), the actual current necessary is greater than 0.1 A.

Exercise \(\PageIndex{2}\)

A typical aluminum soft-drink can weighs about 29 g. How much time is needed to produce this amount of Al(s) in the Hall–Heroult process, using a current of 15 A to reduce a molten Al₂O₃/Na₃AlF₆ mixture?

Answer

5.8 h

Summary

In electrolysis, an external voltage is applied to drive a nonspontaneous reaction. The quantity of material oxidized or reduced can be calculated from the stoichiometry of the reaction and the amount of charge transferred. Relationship of charge, current and time:

\[ C = A \times t \nonumber\]

In electrolysis, an external voltage is applied to drive a nonspontaneous reaction. Electrolysis can also be used to produce H₂ and O₂ from water. In practice, an additional voltage, called an overvoltage, must be applied to overcome factors such as a large activation energy and a junction potential. Electroplating is the process by which a second metal is deposited on a metal surface, thereby enhancing an object’s appearance or providing protection from corrosion. The amount of material consumed or produced in a reaction can be calculated from the stoichiometry of an electrolysis reaction, the amount of current passed, and the duration of the electrolytic reaction.