7.7: Coupled Reactions

Learning Objectives

Endergonic reactions can also be pushed by coupling them to another reaction, which is strongly exergonic, often through shared intermediates.

Many chemicals' reactions are endergonic (i.e., not spontaneous (\(\Delta G > 0\))) and require energy to be externally applied to occur. However, these reaction can be coupled to a separate, exergonic (thermodynamically favorable \(\Delta G <0\)) reactions that 'drive' the thermodynamically unfavorable one by coupling or 'mechanistically joining' the two reactions often via a share intermediate. Since Gibbs Energy is a state function, the \(\Delta G\) values for each half-reaction may be summed, to yield the combined \(\Delta G\) of the coupled reaction.

One simple example of the coupling of reaction is the decomposition of calcium carbonate:

\[CaCO_{3(s)} \rightleftharpoons CaO_{(s)} + CO_{2(g)} \;\;\;\;\;\;\; \Delta G^o = 130.40 \;kJ/mol \label{1}\]

The strongly positive \(\Delta G\) for this reaction is reactant-favored. If the temperature is raised above 837 ºC, this reaction becomes spontaneous and favors the products. Now, let's consider a second and completely different reaction that can be coupled ot this reaction. The combustion of coal released by burning the coal \(\Delta G^o = -394.36 \;kJ/mol\) is greater than the energy required to decompose calcium carbonate (\(\Delta G^o = 130.40 \;kJ/mo\)).

\[C_{(s)} + O_2 \rightleftharpoons CO_{2(g)} \;\;\;\;\;\;\; \Delta G^o = -394.36 \;kJ/mol \label{2}\]

If reactions \(\ref{1}\) and \(\ref{2}\) were added

\[CaCO_{3(s)} + C_{(s)} + O_2 \rightleftharpoons CaO_{(s)} + 2CO_[{2(g)} \;\;\;\; \Delta G^o = -263.96 \;kJ/mol \label{3}\] and then Hess's Law were applied, the combined reaction (Equation \(\ref{3}\)) is product-favored with \(\Delta G^o = -263.96 \;kJ/mol\). This is because the reactant-favored reaction (Equation \(\ref{2}\)) is linked to a strong spontaneous reaction so that both reactions yield products. Notice that the \(\Delta G\) for the coupled reaction is the sum of the constituent reactions; this is a consequence of Gibbs energy being a state function:

\[\Delta G^o = 130.40 \;kJ/mol+ -394.36 \;kJ/mol = -263.96 \;kJ/mol\]

Coupled Reactions in Biology

This is a common feature in biological systems where some enzyme-catalyzed reactions are interpretable as two coupled half-reactions, one spontaneous and the other non-spontaneous. Organisms often the hydrolysis of ATP (adenosine triphosphate) to generate ADP (adenosine diphosphate) as the spontaneous coupling reaction (Figure \(\PageIndex{1}\)).

\[ATP + H_2O \rightleftharpoons ADP + P_i \label{4}\]

• \(P_i\) is inorganic phosphate ion

The phosphoanhydride bonds formed by ejecting water between two phosphate group of ATP exhibit a large negative \(-\Delta G\) of hydrolysis and are thus often termed "high energy" bonds. However, as with all bonds, energy is requires to break these bonds, but the thermodynamic Gibbs energy difference is strongly "energy releasing" when including the solvation thermodynamics of the phosphate ions; \(\Delta G \) for this reaction is - 31 kJ/mol.

Figure \(\PageIndex{1}\): Hydrolysis of ATP to Form ADP

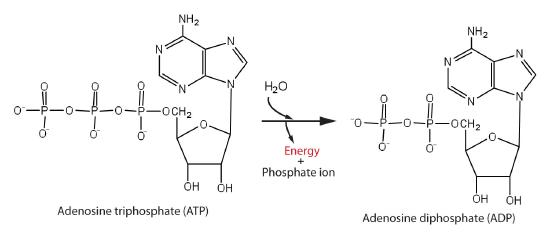
ATP is the major 'energy' molecule produced by metabolism, and it serves as a sort of 'energy source' in cell: ATP is dispatched to wherever a non-spontaneous reaction needs to occurs so that the two reactions are coupled so that the overall reaction is thermodynamically favored.

Example \(\PageIndex{1}\): Phosphorylating Carboxylic Acids

Aldehydes \(RCHO\) are organic compounds that can be oxidized to generate carboxylic acids and nicotinamide adenine dinucleotide (NAD) is a coenzyme found in all living cells and in the reduced form, \(NAD^+\), it acts as an oxidizing agent that can accept electrons from other molecules.

The NAD⁺-linked oxidation of an aldehyde is practically irreversible with an equilibrium that strongly favors the products (\(\Delta G >> 0\):

\[RCHO + NAD^+ + H_2O \rightleftharpoons RCOOH + NADH + H^+ \label{Spontaneous}\]

The position of equilibrium for phosphorylating carboxylic acids lies very much to the left:

\[RCOOH + P_i \rightleftharpoons RC(=O)(O-P_i) + H_2O \label{Nonspontaneous}\]

• (P_i\) is inorganic phosphate ion.

The non-spontaneous formation of a phosphorylated carboxylic acid can be driven by coupling it to the (spontaneous) NAD⁺-linked oxidation of an aldehyde?

Figure \(\PageIndex{2}\): A reaction will not proceed spontaneously unless the products of the reaction have lower energy than the reactants. This is called an exergonic reactions. A reaction where the products have higher energy than the reactions (energonic reaction) can only proceed when there is an input of energy. Exergonic reactions like burning of glucose drives ATP synthesis. The ATP molecules are used to power other endergonic reactions like protein synthesis. from Wikipedia (Muessig).

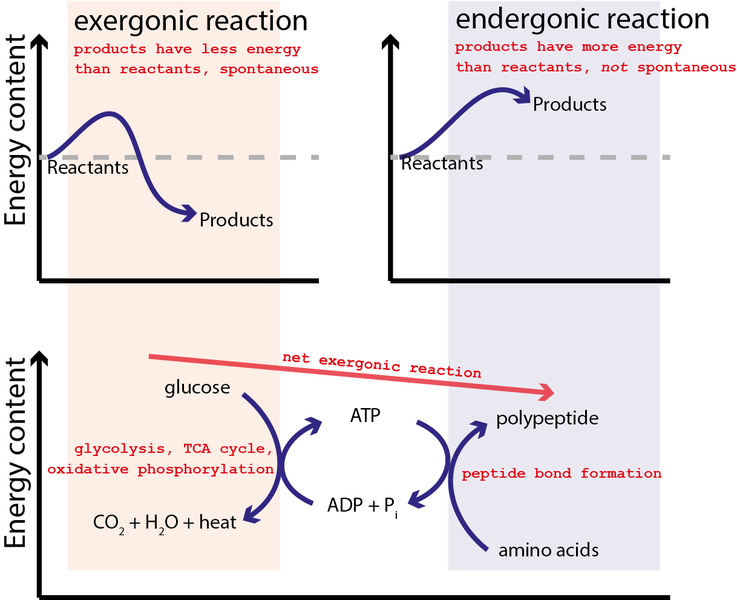
Similarly, ATP hydrolysis can be used to combine amino acids together to generate polypeptides (and proteins) as graphically illustrated by Figure \(\PageIndex{2}\). In this case, the reverse of Equation \(\ref{4}\) is initially coupled to the oxidizing glucose by oxygen

\[C_6H_{12}O_6 + 6O_2 \rightarrow 6CO_2 + 6H_2O \label{5}\] Reaction \(\ref{5}\) is strongly spontaneous with \(\Delta G = −2880 \;kJ/mol \) or close to 100x greater energy capability than the hydrolysis of ATP in Equation \(\ref{4}\). Hence, the equilibrium for this reaction so strongly favors the products that a single arrow is typically used in the chemical equation as it is essential irreversible. It may not be surpising that glucose and all sugars are very energetic moleculess since they are the primary energy source for life.

References

1. Damitio , J., Smith , G., Meany , J. E., Pocker, Y. (1992). A comparative study of the enolization of pyruvate and the reversible dehydration of pyruvate hydrate J. Am. Chem. Soc., 114, 3081–3087
2. Pocker, Y., Meany, J. E., Nist, B. J., & Zadorojny, C. (1969) The Reversible Hydration of Pyruvic Acid. I. Equilibrium Studies. J. Phys. Chem. 76, 2879 – 2882.
3. Waslh, C. (1979) Enzymatic Reaction Mechanisms. W.H. Freeman & Co.

Summary

Two (or more) reactions may be combined such that a spontaneous reaction may be made 'drive' an nonspontaneous one. Such reactions may be considered coupled. Changes in Gibbs energy of the coupled reactions are additive.

Contributors and Attributions

• Stackexcahnge (TomD)