11.03: Organization of Electrons in Atoms

Last updated
Save as PDF

Page ID: 178174

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Learning Objectives

Learn how electrons are organized in atoms.
Represent the organization of electrons by an electron configuration.

We learned in 11.02: Quantum Numbers for Electrons that each electron in an atom has its own unique set of quantum numbers. We also learned electrons will take on the lowest available n value possible and that we can fit up to two electrons in each orbital (with the number of allowed m_ℓ values telling us how many orbitals are available for each value of ℓ). Reading through the previous section keeping track of the allowed quantum numbers for all the electrons in an atom probably seemed like an impossible task. While not impossible it is very complicated, when faced with a complicated and frustrating problem the scientists first line of defense is to create a system to simplify things. In this section we'll learn about the relative energies for our n quantum numbers and a much easier system for keeping track of where our electrons are.

Orbital Energies and Atomic Structure

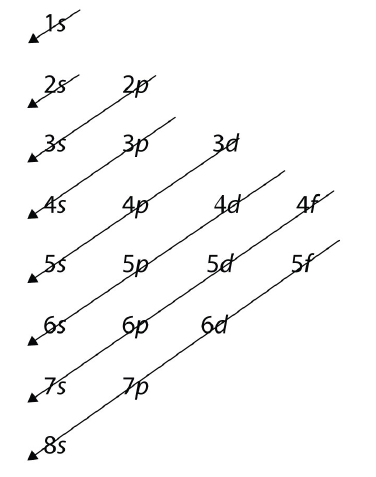
The energy of atomic orbitals increases as the principal quantum number, \(n\), increases. In any atom with two or more electrons, the repulsion between the electrons makes energies of subshells with different values of \(l\) differ so that the energy of the orbitals increases within a shell in the order s < p < d < f. Figure \(\PageIndex{1}\) depicts how these two trends in increasing energy relate. The 1s orbital at the bottom of the diagram is the orbital with electrons of lowest energy. The energy increases as we move up to the 2s and then 2p, 3s, and 3p orbitals, showing that the increasing n value has more influence on energy than the increasing l value for small atoms. However, this pattern does not hold for larger atoms. The 3d orbital is higher in energy than the 4s orbital. Such overlaps continue to occur frequently as we move up the chart.

Figure \(\PageIndex{1}\): Generalized energy-level diagram for atomic orbitals in an atom with two or more electrons (not to scale).

Now that we see how electrons are partitioned among the shells and subshells, we need a more concise way of communicating this partitioning. Chemists use an electronic configuration to represent the organization of electrons in shells and subshells in an atom. An electron configuration simply lists the shell and subshell labels, with a right superscript giving the number of electrons in that subshell. The shells and subshells are listed in the order of filling.

For example, an H atom has a single electron in the 1s subshell. Its electron configuration is

H: 1s¹

He has two electrons in the 1s subshell. Its electron configuration is

He: 1s²

The three electrons for Li are arranged in the 1s subshell (two electrons) and the 2s subshell (one electron). The electron configuration of Li is

Li: 1s²2s¹

Be has four electrons, two in the 1s subshell and two in the 2s subshell. Its electron configuration is

Be: 1s²2s²

Now that the 2s subshell is filled, electrons in larger atoms must go into the 2p subshell, which can hold a maximum of six electrons. The next six elements progressively fill up the 2p subshell:

B: 1s²2s²2p¹
C: 1s²2s²2p²
N: 1s²2s²2p³
O: 1s²2s²2p⁴
F: 1s²2s²2p⁵
Ne: 1s²2s²2p⁶

Now that the 2p subshell is filled (all possible subshells in the n = 2 shell), the next electron for the next-larger atom must go into the n = 3 shell, s subshell.

Example \(\PageIndex{2}\): Sodium

What is the electron configuration for Na, which has 11 electrons?

Solution

The first two electrons occupy the 1s subshell. The next two occupy the 2s subshell, while the next six electrons occupy the 2p subshell. This gives us 10 electrons so far, with 1 electron left. This last electron goes into the n = 3 shell, s subshell. Thus, the electron configuration of Na is 1s²2s²2p⁶3s¹.

Exercise \(\PageIndex{2}\): Magnesium

What is the electron configuration for Mg, which has 12 electrons?

Answer

1s²2s²2p⁶3s²

Orbital Electron Configurations

We will now construct the ground-state electron configuration and orbital diagram for a selection of atoms in the first and second periods of the periodic table. Orbital diagrams are pictorial representations of the electron configuration, showing the individual orbitals and the pairing arrangement of electrons. We start with a single hydrogen atom (atomic number 1), which consists of one proton and one electron. Referring to either Figure \(\PageIndex{3}\) or \(\PageIndex{4}\), we would expect to find the electron in the 1s orbital. By convention, the \(m_s=+\dfrac{1}{2}\) value is usually filled first. The electron configuration and the orbital diagram are:

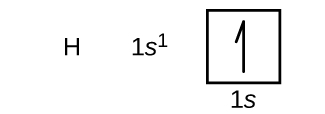
Following hydrogen is the noble gas helium, which has an atomic number of 2. The helium atom contains two protons and two electrons. The first electron has the same four quantum numbers as the hydrogen atom electron (n = 1, l = 0, m_l = 0, \(m_s=+\dfrac{1}{2}\)). The second electron also goes into the 1s orbital and fills that orbital. The second electron has the same n, l, and m_l quantum numbers, but must have the opposite spin quantum number, \(m_s=−\dfrac{1}{2}\). This is in accord with the Pauli exclusion principle: No two electrons in the same atom can have the same set of four quantum numbers. For orbital diagrams, this means two arrows go in each box (representing two electrons in each orbital) and the arrows must point in opposite directions (representing paired spins). The electron configuration and orbital diagram of helium are:

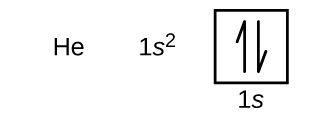
In this figure, the element symbol He is followed by the electron configuration, “1 s superscript 2.” An orbital diagram is provided that consists of a single square. The square is labeled below as “1 s.” It contains a pair of half arrows: one pointing up and the other down.

The n = 1 shell is completely filled in a helium atom.

The next atom is the alkali metal lithium with an atomic number of 3. The first two electrons in lithium fill the 1s orbital and have the same sets of four quantum numbers as the two electrons in helium. The remaining electron must occupy the orbital of next lowest energy, the 2s orbital ( Figure \(\PageIndex{3}\) or \(\PageIndex{4}\) ). Thus, the electron configuration and orbital diagram of lithium are:

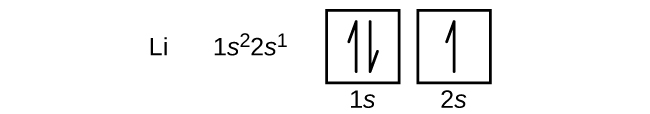
An atom of the alkaline earth metal beryllium, with an atomic number of 4, contains four protons in the nucleus and four electrons surrounding the nucleus. The fourth electron fills the remaining space in the 2s orbital.

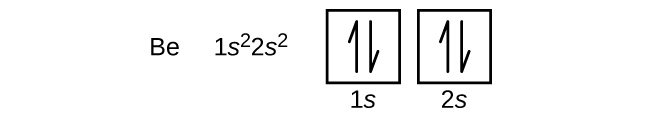
In this figure, the element symbol B e is followed by the electron configuration, “1 s superscript 2 2 s superscript 2.” An orbital diagram is provided that consists of two individual squares. The first square is labeled below as, “1 s.” The second square is similarly labeled, “2 s.” Both squares contain a pair of half arrows: one pointing up and the other down.

An atom of boron (atomic number 5) contains five electrons. The n = 1 shell is filled with two electrons and three electrons will occupy the n = 2 shell. Because any s subshell can contain only two electrons, the fifth electron must occupy the next energy level, which will be a 2p orbital. There are three degenerate 2p orbitals (m_l = −1, 0, +1) and the electron can occupy any one of these p orbitals. When drawing orbital diagrams, we include empty boxes to depict any empty orbitals in the same subshell that we are filling.

Carbon (atomic number 6) has six electrons. Four of them fill the 1s and 2s orbitals. The remaining two electrons occupy the 2p subshell. We now have a choice of filling one of the 2p orbitals and pairing the electrons or of leaving the electrons unpaired in two different, but degenerate, p orbitals. The orbitals are filled as described by Hund’s rule: the lowest-energy configuration for an atom with electrons within a set of degenerate orbitals is that having the maximum number of unpaired electrons. Thus, the two electrons in the carbon 2p orbitals have identical n, l, and m_s quantum numbers and differ in their m_l quantum number (in accord with the Pauli exclusion principle). The electron configuration and orbital diagram for carbon are:

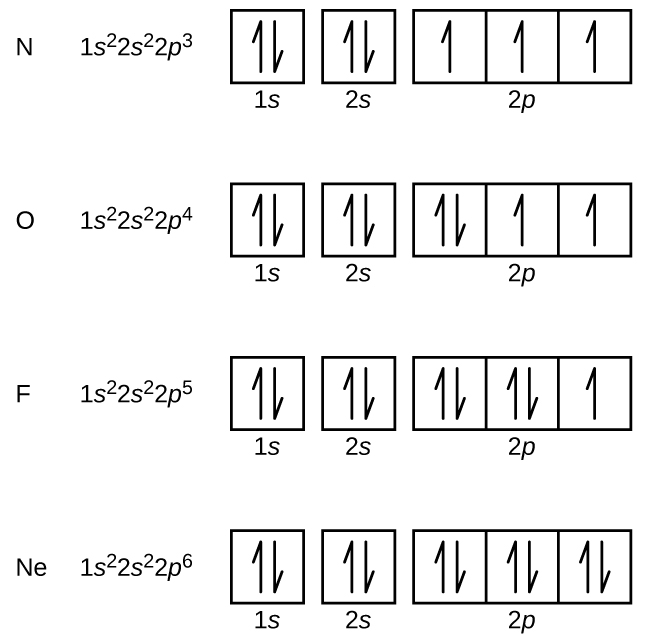
Nitrogen (atomic number 7) fills the 1s and 2s subshells and has one electron in each of the three 2p orbitals, in accordance with Hund’s rule. These three electrons have unpaired spins. Oxygen (atomic number 8) has a pair of electrons in any one of the 2p orbitals (the electrons have opposite spins) and a single electron in each of the other two. Fluorine (atomic number 9) has only one 2p orbital containing an unpaired electron. All of the electrons in the noble gas neon (atomic number 10) are paired, and all of the orbitals in the n = 1 and the n = 2 shells are filled. The electron configurations and orbital diagrams of these four elements are:

Larger Atoms Electron Configurations

For larger atoms, the electron arrangement becomes more complicated. This is because after the 3p subshell is filled, filling the 4s subshell first actually leads to a lesser overall energy than filling the 3d subshell. Recall that while the principal quantum number largely dictates the energy of an electron, the angular momentum quantum number also has an impact on energy; by the time we get to the 3d and 4s subshells, we see overlap in the filling of the shells (Figure \(\PageIndex{1}\) Thus, after the 3p subshell is completely filled (which occurs for Ar), the next electron for K occupies the 4s subshell, not the 3d subshell:

K: 1s²2s²2p⁶3s²3p⁶4s¹,

not

K: 1s²2s²2p⁶3s²3p⁶3d¹

For larger and larger atoms, the order of filling the shells and subshells seems to become even more complicated. There are some useful ways to remember the order, like that shown in Figure \(\PageIndex{1}\). If you follow the arrows in order, they pass through the subshells in the order that they are filled with electrons in larger atoms. Initially, the order is the same as the expected shell-subshell order, but for larger atoms, there is some shifting around of the principal quantum numbers. However Figure \(\PageIndex{1}\) gives a valid ordering of filling subshells with electrons for most atoms.

Figure \(\PageIndex{1}\) Electron Shell Filling Order. Starting with the top arrow, follow each arrow. The subshells you reach along each arrow give the ordering of filling of subshells in larger atoms. The n = 5 and higher shells have more subshells, but only those subshells that are needed to accommodate the electrons of the known elements are given.

Example \(\PageIndex{3}\): Tin

What is the predicted electron configuration for Sn, which has 50 electrons?

Solution

We will follow the chart in Fig. 8.4., until we can accommodate 50 electrons in the subshells in the proper order:Sn: 1s²2s²2p⁶3s²3p⁶4s²3d¹⁰4p⁶5s²4d¹⁰5p²

Verify by adding the superscripts, which indicate the number of electrons: 2 + 2 + 6 + 2 + 6 + 2 + 10 + 6 + 2 + 10 + 2 = 50, so we have placed all 50 electrons in subshells in the proper order.

Exercise \(\PageIndex{3}\): Barium

What is the electron configuration for Ba, which has 56 electrons?

Answer

1s²2s²2p⁶3s²3p⁶4s²3d¹⁰4p⁶5s²4d¹⁰5p⁶6s²

Abbreviated Electron Configurations

As the previous example demonstrated, electron configurations can get fairly long. An abbreviated electron configuration uses one of the elements from the last column of the periodic table, which contains what are called the noble gases, to represent the core of electrons up to that element. Then the remaining electrons are listed explicitly. For example, the abbreviated electron configuration for Li, which has three electrons, would be

Li: [He]2s¹

where [He] represents the two-electron core that is equivalent to He's electron configuration. The square brackets represent the electron configuration of a noble gas. This is not much of an abbreviation. However, consider the abbreviated electron configuration for W, which has 74 electrons:

W: [Xe]6s²4f¹⁴5d⁴

This is a significant simplification over an explicit listing of all 74 electrons. So for larger elements, the abbreviated electron configuration can be a very useful shorthand.

Example \(\PageIndex{4}\): Phosphorus

What is the abbreviated electron configuration for P, which has 15 electrons?

Solution

With 15 electrons, the electron configuration of P is

P: 1s²2s²2p⁶3s²3p³

The first immediate noble gas is Ne, which has an electron configuration of 1s²2s²2p⁶. Using the electron configuration of Ne to represent the first 10 electrons, the abbreviated electron configuration of P is

P: [Ne]3s²3p³

Exercise \(\PageIndex{4}\): Rubidium

What is the abbreviated electron configuration for Rb, which has 37 electrons?

Answer

[Kr]5s¹

There are some exceptions to the rigorous filling of subshells by electrons. In many cases, an electron goes from a higher-numbered shell to a lower-numbered but later-filled subshell to fill the later-filled subshell. One example is Ag. With 47 electrons, its electron configuration is predicted to be

Ag: [Kr]5s²4d⁹

However, experiments have shown that the electron configuration is actually

Ag: [Kr]5s¹4d¹⁰

This, then, qualifies as an exception to our expectations. At this point, you do not need to memorize the exceptions; but if you come across one, understand that it is an exception to the normal rules of filling subshells with electrons, which can happen.

Summary

The Pauli exclusion principle limits the number of electrons in the subshells and shells. Electrons in larger atoms fill shells and subshells in a regular pattern that we can follow. Electron configurations are a shorthand method of indicating what subshells electrons occupy in atoms. Abbreviated electron configurations are a simpler way of representing electron configurations for larger atoms. Exceptions to the strict filling of subshells with electrons occur.