9.4: Transmutation
- Page ID
- 236741
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Define transmutation.
- Classify a transmutation a combination or a decomposition reaction.
- Identify the indicator words associated with transmutation reactions.
- Write a balanced nuclear equation that represents the transmutation of two nuclei.
Section 9.2 presented the process for developing the nuclear equation pattern for a radioactive decay reaction, in which a more stable daughter nucleus is generated upon the emission, or release, of radiation by an unstable radioisotope. Furthermore, recall that all elements that have atomic numbers that are greater than 92 are synthesized through a second nuclear reaction, transmutation, in which a new radioisotope is generated by bombarding a stable nucleus with small particles. The following paragraphs will present the process for developing a nuclear equation pattern that symbolically-represents this type of reaction and, subsequently, modifying the pattern that is established to reflect the identities of the specific nuclei that are involved in a particular transformation.
In order to indicate that an irreversible chemical change has occurred, a "forward," or left-to-right, reaction arrow is written in the nuclear equation pattern that is being developed, as shown below. Additionally, since a nuclear equation is the symbolic representation of a nuclear reaction, the nuclear symbols, not the names, of the particles that are reacted and produced are incorporated into this pattern. Based on the definition of transmutation that is provided above, this nuclear process can be classified as a combination reaction, and, therefore, the nuclear symbol for a single product, the new radioisotope, is written on the right side of the reaction arrow. Two reactants, which can be nuclei or other small particles, should be represented on the left side of the arrow, and a plus sign, "+", must be used to separate their corresponding nuclear symbols, which can be written in any order. Additionally, while one of four types of radiation, which can be generically-defined as small particles or bursts of energy that are emitted from an unstable radioisotope, must be produced during a radioactive decay reaction, radiation is not necessarily generated during a transmutation reaction, since the new radioisotope that is produced may not subsequently decompose. Finally, in order to indicate that the equation pattern that is shown below should be applied to symbolically-represent a transmutation reaction, in which nuclear particles are forced to collide with one another at high speeds, a word such as "collide," "collides," "collided," "colliding," or "collision" must be included in the verbal description of a specific transmutation reaction.
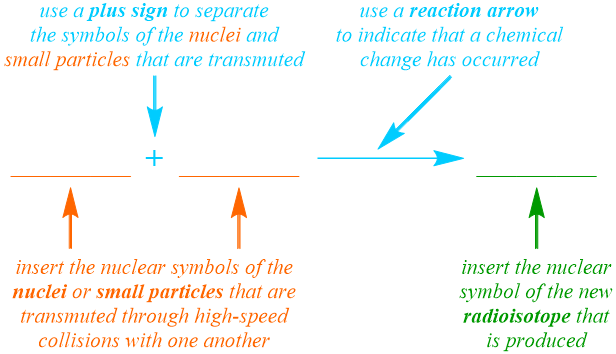
As stated above, the product that is synthesized during a transmutation reaction is a new radioisotope. In order to identify the element that is generated, the nuclear equation that is being developed must be "balanced." Recall that the Law of Conservation of Matter is a fundamental principle that mandates that particles cannot be created or destroyed in the course of a chemical change. Consequently, while the elemental symbols of substances must change during a nuclear reaction, the relative quantity of protons and neutrons that are involved in the reaction must be constant. As stated previously, the atomic number of an element is defined as the number of protons that are contained in an atom of that element, and the mass number of a particular elemental isotope is calculated by adding the quantities of protons and neutrons that are present in that atom. Therefore, since the atomic number and mass number of an isotope are written as the subscript and superscript, respectively, in the nuclear symbol that is used to represent that isotope, a nuclear equation is "balanced" if the sums of the atomic numbers and the mass numbers on the reactant side of the arrow are equal to the corresponding totals on the product side of the equation. As a result, the atomic number and mass number of the new radioisotope must be calculated by adding the atomic numbers and mass numbers, respectively, of the nuclei or other small particles that were initially present. Furthermore, since the atomic number of an element is a unique value that directly corresponds to the identity of that element, the calculated subscript should be used to determine which elemental symbol represents the new radioisotope that is produced in a particular transmutation reaction. Finally, because the Law of Conservation of Matter is upheld by calculating the atomic number and mass number of the new radioisotope, balancing coefficients are rarely incorporated into nuclear equations.
For example, write a balanced nuclear equation that represents the collision of helium-4 and nitrogen-14.
Because the word "collision" is included in the given statement, the nuclear equation pattern that corresponds to a transmutation should be applied to symbolically-represent this reaction. Since a transmutation is a combination reaction, a single product should be written on the right side of the reaction arrow, and two reactants, separated by a plus sign, "+", should be represented on the left side of the equation, as shown below.
_____ + _____ \(\rightarrow\) _____
The reactants in a transmutation reaction are nuclei or other small particles. Since the statement indicates that the collision of helium-4 and nitrogen-14 should be represented in the equation that is being developed, these nuclei are the reactants in the corresponding reaction. Since nuclear symbols must be incorporated into a nuclear equation, the symbolisms that correspond to these nuclei, "\(\ce{^{4}_{2}He}\)" and "\(\ce{^{14}_{7}N}\)," respectively, are written on the left side of this pattern, as shown below. The subscripts in these symbolisms, 2 and 7, respectively, are determined by locating helium and nitrogen on the periodic table and recording the atomic numbers that correspond to these elements.
\(\ce{^{4}_{2}He}\) + \(\ce{^{14}_{7}N}\) \(\rightarrow\) _____
Finally, in order to identify the new radioisotope that is generated, the nuclear equation that is written above must be "balanced." Recall that the Law of Conservation of Matter mandates that particles cannot be created or destroyed in the course of a chemical change. Consequently, while the elemental symbols of substances must change during a nuclear reaction, the relative quantity of protons and neutrons that are involved in the reaction must be constant. As stated previously, the atomic number of an element is defined as the number of protons contained in an atom of that element, and the mass number of a particular elemental isotope is calculated by adding the quantities of protons and neutrons that are present in that atom. Therefore, since the atomic number and mass number of an isotope are written as the subscript and superscript, respectively, in the nuclear symbol that is used to represent that isotope, a nuclear equation is "balanced" if the sums of the atomic numbers and the mass numbers on the reactant side of the arrow are equal to the corresponding totals on the product side of the equation. The atomic number of the new radioisotope, 9, is calculated by adding the atomic numbers, 2 and 7, respectively, of the nuclei that were initially present. Furthermore, since the atomic number of an element is a unique value that directly corresponds to the identity of that element, this calculated subscript indicates that the new radioisotope that is produced in this transmutation reaction, fluorine, is symbolized as "F." The mass number of the new radioisotope, 18, is calculated by adding the mass numbers, 4 and 14, respectively, of the nuclei that are collided with one another. Finally, since the Law of Conservation of Matter is upheld by calculating the atomic number and mass number of the new radioisotope, balancing coefficients are not incorporated into the nuclear equation that is shown below. Because the following reaction equation is balanced, this nuclear equation is the chemically-correct representation of the collision of helium-4 and nitrogen-14.
\(\ce{^{4}_{2}He}\) + \(\ce{^{14}_{7}N}\) \(\rightarrow\) \(\ce{^{18}_{9}F}\)
Write a balanced nuclear equation that represents the collision of two oxygen-16 nuclei.
- Answer
- Because the word "collision" is included in the given statement, the nuclear equation pattern that corresponds to a transmutation should be applied to symbolically-represent this reaction. Since a transmutation is a combination reaction, a single product should be written on the right side of the reaction arrow, and two reactants, separated by a plus sign, "+", should be represented on the left side of the equation. Furthermore, the reactants in a transmutation reaction are nuclei or other small particles. Because the statement indicates that the collision of two oxygen-16 nuclei should be represented in the equation that is being developed, these particles are the reactants in the corresponding reaction. Since nuclear symbols must be incorporated into a nuclear equation, the symbolism "\(\ce{^{16}_{8}O}\)" is written in both positions on the left side of this pattern, as shown below.
\(\ce{^{16}_{8}O}\) + \(\ce{^{16}_{8}O}\) \(\rightarrow\) _____
Finally, in order to identify the new radioisotope that is generated, the nuclear equation that is written above must be "balanced" by equating the sums of the atomic number subscripts and the mass number superscripts on the reactant side of the arrow to the corresponding totals on the product side of the equation. The atomic number of the new radioisotope, 16, is calculated by adding the atomic numbers, 8 and 8, respectively, of the nuclei that were initially present. Furthermore, since the atomic number of an element directly corresponds to the identity of that element, this calculated subscript indicates that the new radioisotope that is produced in this transmutation reaction, sulfur, is symbolized as "S." The mass number of the new radioisotope, 32, is calculated by adding the mass numbers, 16 and 16, respectively, of the nuclei that are collided with one another. Finally, since the Law of Conservation of Matter is upheld by calculating the atomic number and mass number of the new radioisotope, balancing coefficients are not incorporated into the nuclear equation that is shown below. Because the following reaction equation is balanced, this nuclear equation is the chemically-correct representation of the collision of two oxygen-16 nuclei.\(\ce{^{16}_{8}O}\) + \(\ce{^{16}_{8}O}\) \(\rightarrow\) \(\ce{^{32}_{8}S}\)
Write a balanced nuclear equation that represents the reaction that generates beryllium-10 through the collision of beryllium-9 with a subatomic particle.
- Answer
- Because the word "collision" is included in the given statement, the nuclear equation pattern that corresponds to a transmutation should be applied to symbolically-represent this reaction. Since a transmutation is a combination reaction, a single product should be written on the right side of the reaction arrow, and two reactants, separated by a plus sign, "+", should be represented on the left side of the equation. Because the given statement indicates that the generation of beryllium-10 should be represented in the equation that is being developed, the new radioisotope that is produced in the corresponding reaction is a beryllium-10 nucleus. Furthermore, since the statement indicates that the collision of beryllium-9 and a subatomic particle should be symbolized in this equation, these substances are the reactants in the corresponding reaction. Because nuclear symbols must be incorporated into a nuclear equation, the symbolisms "\(\ce{^{10}_{4}Be}\)" and "\(\ce{^{9}_{4}Be}\)" are written on the right and left sides of this pattern, respectively, as shown below.
\(\ce{^{9}_{4}Be}\) + _____ \(\rightarrow\) \(\ce{^{10}_{4}Be}\)
Finally, in order to identify the subatomic particle that is collided with beryllium-9, the nuclear equation that is written above must be "balanced" by equating the sums of the atomic number subscripts and the mass number superscripts on the reactant side of the arrow to the corresponding totals on the product side of the equation. The atomic number of the subatomic particle, 0, is calculated by subtracting the atomic number of the nucleus that was initially present, 4, from the atomic number of the new radioisotope that is generated, 4. The atomic number of an element directly corresponds to the identity of that element. However, this calculated subscript does not correspond to any elements that are present on the periodic table. The mass number of the subatomic particle, 1, is calculated by subtracting the atomic number of the nucleus that was initially present, 9, from the atomic number of the new radioisotope that is generated, 10. Based on these calculated values, the subatomic particle that is collided with beryllium-9 has an atomic number of 0 and a mass number of 1 and, therefore, contains 0 protons and 1 neutron. Consequently, the subatomic particle that participates in this transmutation reaction is a neutron. The "elemental symbol" that is written in the corresponding nuclear symbol for this particle, "\(\ce{^{1}_{0}n}\)," is derived from the subatomic particle symbolism for a neutron, "n0." Finally, since the Law of Conservation of Matter is upheld by calculating the atomic number and mass number of the subatomic particle that is collided with beryllium-9, balancing coefficients are not incorporated into the nuclear equation that is shown below. Because the following reaction equation is balanced, this nuclear equation is the chemically-correct representation of the reaction that generates beryllium-10 through the collision of beryllium-9 and a neutron.\(\ce{^{9}_{4}Be}\) + \(\ce{^{1}_{0}n}\) \(\rightarrow\) \(\ce{^{10}_{4}Be}\)

