9.1: Nuclear Particles: Review and Reactivity
- Page ID
- 213293
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Write the nuclear symbol of a given elemental isotope.
- Define radioisotope.
- Define nuclear equation.
The three main subatomic particles, electrons, protons, and neutrons, were first defined and discussed in Chapter 2. Recall that electrons are located in orbitals, which are defined regions in space that occupy the majority of the volume in an atom. Furthermore, the bonding interactions and chemical reactivity of an element is solely-determined by the number of valence electrons, which are found in the highest-energy orbitals, that are present in an atom of that element. Electrons, which are symbolized as "e–," remain anchored in atoms due to their electrostatic attraction to the protons that are located in the nucleus, which is the densely-packed space at the center of an atom. The atomic number of an element, which is written above the elemental symbol in a box on the periodic table, is a unique value that directly corresponds to the the identity of that element and, furthermore, defines the number of protons that exist in every atom of that element. In order to remain electrically-neutral, an atom must contain an equal number of protons, which bear +1 charges, and electrons, which bear –1 charges.
However, each positively-charged proton is strongly repelled by every other proton that is present in an atom, and, furthermore, the combined strength of these repulsive forces is substantial enough to splinter the nucleus. The final subatomic particles, which, due to their neutral charges, are called neutrons, are also located in the nucleus of an atom and effectively act as "nuclear glue" that allows the protons to exist in close physical proximity to one another. The number of neutrons, which are symbolized as "n0," that are found in an atom is not defined by the atomic number of that element and, therefore, can vary from atom to atom. Altering the number of neutrons that are present in an atom creates unique elemental isotopes, which are atoms that contain the same number of protons, but differ in the quantity of neutrons that are present in the corresponding nuclei. Alternatively, isotopes can be defined as atoms that have the same atomic numbers, but have different different mass numbers, which are calculated by adding the number of protons and neutrons that are contained in the nucleus of an atom.
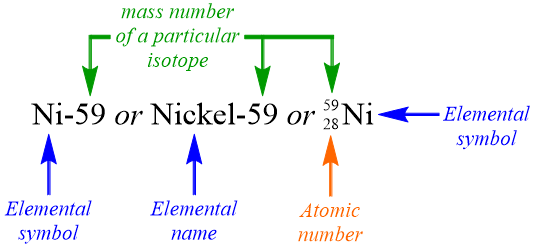
Recall that scientists utilize three different elemental symbolisms to refer to specific elemental isotopes. The first two symbolisms are very similar, in that each includes the elemental name, or elemental symbol, of an element, followed by a dash and a numerical value, which corresponds to the mass number of a particular isotope of that element. In the third type of elemental symbolism, which is called a nuclear symbol, the mass number of the isotope is positioned as a superscript before an elemental symbol, and the atomic number of the element is written directly underneath the mass number. It is important to note the difference between an isotope and an elemental symbolism. Figure \(\PageIndex{1}\) models these three different elemental symbolisms, which all represent the same isotope, since each has an identical mass number.
Write the nuclear symbol of each of the following isotopes.
- Sulfur-32
- In-117
- Answer a
- In a nuclear symbol, the mass number of the isotope is positioned as a superscript before an elemental symbol, and the atomic number of the element is written directly underneath the mass number. The element that is referenced in the given symbolism, sulfur, S, has an atomic number of 16, and the number that is written after the dash in this notation, 32, corresponds to the mass number of the specific isotope that is being considered. The nuclear symbol shown below is generated by representing this information into the format that is described above.
\(\ce{^{32}_{16}S}\)
- Answer b
- In a nuclear symbol, the mass number of the isotope is positioned as a superscript before an elemental symbol, and the atomic number of the element is written directly underneath the mass number. The element that is referenced in the given symbolism, In, indium, has an atomic number of 49, and the number that is written after the dash in this notation, 117, corresponds to the mass number of the specific isotope that is being considered. The nuclear symbol shown below is generated by representing this information into the format that is described above.
\(\ce{^{117}_{49}In}\)
In order to overcome the repulsive forces that exist between protons and, therefore, hold the nucleus together, a minimum number of neutrons must be present in every atom of a particular element. However, while the the presence of a small number of additional neutrons in a nucleus does not sacrifice the structural integrity of that atom, a nucleus that contains too many neutrons is unstable and, consequently, decomposes through a process called radioactive decay, which will be discussed in detail in the following section of this chapter. Due to the large number of subatomic particles that are contained in their corresponding nuclei, nearly all of the elements that have atomic numbers greater than 20 have at least one unstable isotope, which is known as a radioisotope. Finally, nuclei that contain more than 240 protons and neutrons, in total, are prohibitively-large and are, correspondingly, highly unstable. As a result, uranium, U, which has an atomic number of 92, is the last element that has been isolated from natural sources. All subsequent elements are generated through a second nuclear reaction, transmutation, which will also be described in a later section of this chapter.
Radioactive decay and transmutation reactions can be symbolically-represented using nuclear equations. As both of these processes involve unique nuclear interactions, the equations that represent these transformations must also be distinctive. Furthermore, because many different elements can participate in nuclear reactions, the identities of the atoms that are involved in a particular radioactive decay or transmutation reaction must be incorporated into the corresponding equation that is written to symbolize the change that is occurring. Therefore, a generic nuclear equation pattern, which can be modified to include the symbols of the specific nuclei that are involved in a particular transformation, will be presented and applied for both radioactive decay or transmutation reactions. Finally, in order to indicate which equation pattern should be applied to symbolically-represent a particular transformation, a unique key word must be included in the verbal descriptions that correspond to each of these types of nuclear reactions.

