9.5: Fission and Fusion
- Page ID
- 213298
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Define fission reaction.
- Define chain reaction.
- Define fusion reaction.
- Classify a nuclear reaction as a fission reaction or a fusion reaction.
As stated previously, a radioisotope is defined as a nucleus that contains too many neutrons and, therefore, is highly unstable. In order to generate a more stable daughter nucleus, a radioisotope must emit, or release, radiation through a process called radioactive decay. A second type of nuclear reaction, known as transmutation, can be used to produce new radioisotopes by bombarding stable nuclei with small particles. By definition, the reactant nuclei that participate in, and the product particles that are generated during, radioactive decay and transmutation reactions must contain different quantities of protons and neutrons. Because the atomic compositions and, therefore, the identities, of these particles are transformed during radioactive decay and transmutation reactions, these nuclear processes can both be classified as chemical changes.
During their investigations of these processes, scientists discovered that the combined mass of the product particles that were generated during a nuclear reaction was smaller than the total mass of the nuclei that were initially present. This observation directly violates the Law of Conservation of Mass, which states that mass cannot be created or destroyed in the course of a chemical change. However, recall that mass and energy are related through Albert Einstein's mass-energy equivalence principle, which is represented in the well-known equation, E = mc2. Therefore, scientists hypothesized, correctly, that this difference in particle mass was offset by an equivalent change in energy. Furthermore, since the Law of Conservation of Energy states that energy also cannot be created or destroyed during a chemical change, the energy that is created during a nuclear reaction cannot simply dissipate and, instead, is released in the form of heat, light, and gamma radiation. Therefore, because heat is generated as a product in radioactive decay and transmutation reactions, these nuclear transformations are classified as exothermic.
Currently, the human population relies heavily on burning fossil fuels, such as coal and oil, in order to generate electricity. Approximately 600 coal-burning electric plants have been constructed in the United States, alone, and these factories produce 48.5% of the power that is used by the American population. However, these industrial complexes also generate more than two billion tons of carbon dioxide, which is a "greenhouse gas" that has been shown to contribute to global warming, as well as other toxic substances, such as sulfur dioxide, nitrous oxide, and mercury. In order to attempt to minimize the amounts of these, and other, harmful chemicals that are synthesized from burning fossil fuels, scientists have been researching, developing, and implementing alternative methods for generating electricity. Due to the high energy "yield" of nuclear transformations, chemists have explored harnessing the energy that is generated during fission and fusion reactions, which are modified versions of radioactive decay and transmutation reactions, respectively. The combustion of coal and oil typically releases approximately 103, or 1,000, kilojoules, kJ, of energy per mole of fuel that is consumed. In comparison, because nuclear processes involve the reactions of protons and neutrons, which exist in very close physical proximity to one another, the amount of energy that is transferred during a nuclear reaction is nearly one million times larger than the energy that is generated in a combustion reaction.
Fission Reactions
In a fission reaction, energy is produced when a single large radioisotope splits into two smaller nuclei and subatomic particles, such as neutrons. Because a single reactant is present in a fission reaction, this transformation can be categorized as a decomposition reaction. Furthermore, while no radiation is generated during a fission reaction, this nuclear process is still classified as a modified radioactive decay reaction.
Nuclear fission was first observed in 1938, when physicists Lise Meitner and Otto Frisch attempted to synthesize a new isotope of uranium, uranium-236, by bombarding uranium-235 nuclei with neutrons. However, the resultant nucleus was incredibly unstable and immediately decomposed into barium-141 and krypton-92. The balanced nuclear equation that represents this reaction sequence is shown below.
\(\ce{^{235}_{92}U} + \ce{^{1}_{0}n} \rightarrow \ce{^{236}_{92}U} \rightarrow \ce{^{141}_{56}Ba} + \ce{^{92}_{36}Kr} + 3 \ce{^{1}_{0}n} + \rm{E}\)
Because a neutron, \(\ce{^1_0n}\), is symbolized in the initial and final portions of the equation that is shown above, this subatomic particle is both consumed as a reactant and regenerated as a product in the overall reaction. The neutron that is emitted can collide with another uranium-235 nucleus, which, in turn, causes the reaction sequence that is shown above to occur for a second time. Since a new neutron is produced and, subsequently, consumed, during each successive reaction cycle, the reaction sequence that is shown above cannot be stopped until all of the uranium-235 nuclei have been consumed. Furthermore, because a product that is generated in each transmutation/fission sequence initiates the next reaction cycle, these complementary nuclear processes are self-sustaining and, therefore, are collectively-classified as a chain reaction.
Finally, recall that, in a typical radioactive decay reaction, a specific type of radiation is emitted from an unstable nucleus, and the remaining subatomic particles that had been contained in that radioisotope generate a daughter nucleus. Therefore, the total number of protons and neutrons that are contained in the products that are created during a radioactive decay reaction correspond to the atomic number and mass number of the radioisotope that was initially present. Consequently, since the Law of Conservation of Matter is upheld by calculating the atomic number and mass number of the daughter nucleus, balancing coefficients are typically not incorporated into radioactive decay reactions. In contrast, the total number of protons and neutrons that are contained in the products of a fission reaction generally do not correspond to the atomic number and mass number of the radioisotope that was initially present. Therefore, in order to ensure that no particles are destroyed during the fission of an unstable nucleus, one or more additional subatomic particles, such as neutrons, are generated during this type of nuclear reaction. As a result, balancing coefficients are often incorporated into fission reactions, in order to indicate the number of subatomic particles that are emitted. The coefficient that is present in the equation that is shown above, 3, indicates that three neutrons, \(\ce{^1_0n}\), are generated as a result of every neutron/uranium-235 collision that initially occurs. Because the neutrons that are produced during a transmutation/fission reaction sequence are consumed to initiate subsequent reaction cycles, the presence of this coefficient is significant. As shown below in Figure \(\PageIndex{1}\), each of the three neutrons are initially generated from a single neutron/uranium-235 collision can collide with another uranium-235 nucleus, and, as a result, nine neutrons are produced during this secondary reaction cycle. Because this reaction sequence cannot be stopped until all of the uranium-235 nuclei have been consumed, the quantity of neutrons that are present in the reaction vessel and, therefore, the number of reactions that occur in each subsequent reaction cycle, will constantly increase.
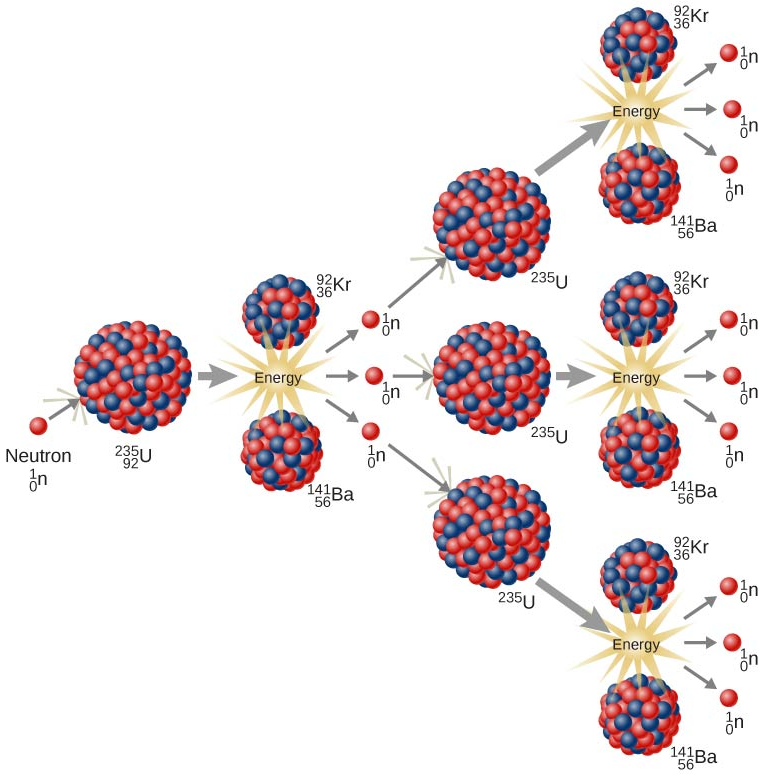
Recall that, by definition, energy is also generated during a fission reaction. Since, as stated above, the number of reactions that occur in each transmutation/fission reaction cycle constantly increases, the amount of energy that is released throughout the reaction process also increases at an exponential rate. Therefore, in order to avoid the accumulation of excess energy inside of a reaction vessel, which is likely to cause an explosion, chain reactions must be performed in specially-designed nuclear reactors. These chambers are constructed using control rods, which absorb some of the neutrons that are generated from each transmutation/fission reaction. Consequently, fewer neutrons are free to collide with uranium-235 nuclei, which, in turn, decreases the number of reactions that occur in the subsequent reaction cycles.
To date, 103 fission reactors have been constructed in the United States. These nuclear facilities produce 19.4% of the power that is used by the American population, and, unlike coal-burning plants, do not generate any greenhouse gases. The amount of energy that is produced in these reactors is currently limited by the availability of uranium-235. Naturally-occurring uranium ore contains 99% uranium-238, by mass. This isotope is relatively stable and, therefore, does not participate in fission reactions. Before uranium ore can be used in a nuclear reaction, the percentage of uranium-235 that is present in a given sample must be tripled through a prohibitively-expensive and time-consuming process called "nuclear enrichment." Therefore, until an alternative enrichment process is developed, the total quantity of energy that is generated from fission reactions will not be competitive with the amount of power that is produced by burning fossil fuels.
Fusion Reactions
In a second type of nuclear process, which is known as a fusion reaction, energy is released when two smaller nuclei collide to produce a larger, more stable atom. Since a single nuclear product is synthesized during a fusion reaction, this transformation can be classified as a modified transmutation reaction. However, a fusion reaction is categorized as a pseudo-combination reaction, rather than a "standard" combination reaction, because of the subatomic particles, such as neutrons, that are also typically generated during this nuclear process.
Recall that two nuclei, which contain protons and, therefore, bear positive charges, will repel when in close physical proximity to one another. This repulsive force, which increases in strength as these particles approach one another, can only be overcome by colliding the reactant nuclei at extremely high velocities, which, in turn, can only be attained at reaction temperatures in excess of one hundred million Kelvin. This temperature is prohibitively-high and, consequently, has not yet been achieved under practical experimental conditions. Furthermore, since all known materials melt, decompose, or ionize at temperatures that are well below this value, a nuclear reactor has not yet been built that can withstand the extreme heat that is required to initiate a fusion reaction.
In contrast to the rarity of uranium-235, which is consumed during fission reactions, the small nuclei that collide with one another in fusion reactions are available in nearly-inexhaustible quantities. Consequently, physicists have hypothesized that, after constructing an appropriate reactor, a limitless supply of energy could be produced using controlled nuclear fusion reactions. As a result, scientists have been designing and analyzing theoretical systems that could be constructed and, subsequently, utilized for performing fusion reactions. Recently, physicists have proposed filling a fusion reactor, like the structure that is shown below in Figure \(\PageIndex{2}\), with plasma, which is a gaseous substance that is composed of ionized particles, and magnetizing the resultant system. Researchers have hypothesized that nuclei that are heated under these experimental conditions would be unable to contact and, therefore, melt, this reaction vessel, which, consequently, could be used to perform a fusion reaction.

While a fusion reaction has not yet been performed on Earth, this nuclear transformation occurs readily on the surface of the sun, where the amount of heat that is generated by gravitational pressure produces temperatures that are well in excess of those that are necessary for overcoming the repulsive force between colliding hydrogen nuclei. The balanced nuclear equation that represents the fusion of deuterium, \(\ce{^2_1H}\), and tritium, \(\ce{^3_1H}\), is shown below. The elemental symbol, H, that represents both of the reactants in this nuclear process corresponds to hydrogen. The atomic mass average of hydrogen, 1.0079, indicates that the most common isotope of this element has a mass number of 1. However, the hydrogen nuclei that are consumed in fusion reactions have mass numbers of 2 and 3, respectively, and, therefore, are known as "heavy hydrogen" isotopes.
\(\ce{^{2}_{1}H} + \ce{^{3}_{1}H} \rightarrow \ce{^{4}_{2}He} + \ce{^{1}_{0}n} + \rm{E}\)
The fusion reaction that is shown above is not a chain reaction, as neither of the reactants that are initially present are regenerated as products. Therefore, for every deuterium/tritium collision that occurs, only a single burst of energy is released. Due to the extremely high stability of the helium-4 nucleus that is produced in this reaction, the energy yield of heavy-hydrogen fusion reactions is approximately 1.7 terajoules, TJ, which is a value that is nearly two billion times more than the energy that is generated in a combustion reaction and is approximately two thousand times greater than the amount of power that is produced in the uranium-235 transmutation/fission reaction that is shown above.
Classify each of the nuclear reactions that are represented in the following equations as a fission reaction or a fusion reaction.
- \(\ce{^{2}_{1}H} + \ce{^{2}_{1}H} \rightarrow \ce{^{3}_{2}He} + \ce{^{1}_{0}n} + \rm{E}\)
- \(\ce{^{235}_{92}U} + \ce{^{1}_{0}n} \rightarrow \ce{^{236}_{92}U} \rightarrow \ce{^{131}_{50}Sn} + \ce{^{103}_{42}Mo} + 2 \ce{^{1}_{0}n} + \rm{E}\)
- \(\ce{^{235}_{92}U} + \ce{^{1}_{0}n} \rightarrow \ce{^{236}_{92}U} \rightarrow \ce{^{139}_{54}Xe} + \ce{^{94}_{38}Sr} + 3 \ce{^{1}_{0}n} + \rm{E}\)
- Answer a
- The nuclear symbols of two small nuclei, \(\ce{^{2}_{1}H}\) and \(\ce{^{2}_{1}H}\), are written on the left side of the reaction arrow, and a single, larger nuclear product, \(\ce{^{3}_{2}He}\), is represented on the product side of this equation. Therefore, this reaction is classified as a fusion.
- Answer b
- The first portion of this reaction sequence, in which two particles combine to form an unstable radioisotope, is categorized as a transmutation reaction. Because this single nucleus, \(\ce{^{236}_{92}U}\), subsequently splits into two smaller nuclei, \(\ce{^{131}_{50}Sn}\) and \(\ce{^{103}_{42}Mo}\), the second part of this reaction sequence is classified as a fission.
- Answer c
- The first portion of this reaction sequence, in which two particles combine to form an unstable radioisotope, is categorized as a transmutation reaction. Because this single nucleus, \(\ce{^{236}_{92}U}\), subsequently splits into two smaller nuclei, \(\ce{^{139}_{54}Xe}\) and \(\ce{^{94}_{38}Sr}\), the second part of this reaction sequence is classified as a fission.

