9.3: Half-Life
- Page ID
- 213296
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Define half-life.
- Calculate the half-life of a radioisotope.
- Calculate the amount of a radioactive sample that has decayed in a specified period of time.
- Calculate the amount of a radioactive sample that remains after a specified period of time has elapsed.
As stated previously, a radioisotope is defined as a nucleus that contains too many neutrons and, therefore, is highly unstable. In order to generate a more stable daughter nucleus, a radioisotope must emit, or release, radiation through a process called radioactive decay. While the decomposition of an individual atom is effectively instantaneous, all of the nuclei that are present in a larger-quantity radioactive sample do not decay simultaneously. The rate at which a radioisotope decays is indirectly, or inversely, proportional to the stability of the nucleus that is being studied. Therefore, less stable nuclei decompose more quickly, and more stable radioisotopes decay over longer periods of time. In order to quantitatively compare the decomposition rates of different nuclei, chemists defined the half-life (t1/2) of a radioisotope to be the amount of time that is required for exactly one-half of a sample of that isotope to decay into more stable daughter nuclei.
Several important applications involve measuring the amount of a radioisotope that has decayed and, subsequently, comparing that value to a quantity that is calculated using the half-life of the nucleus that is being monitored. In order to determine the age of organic, or carbon-based, and inorganic, or non-carbon-containing, materials, respectively, scientists can measure the amounts of carbon-14 and uranium-238 that are present in those substances. Various radioisotopes are used in medicinal screening procedures to establish whether different organs and physiological systems are functioning properly, and additional radioactive materials are used to treat cancers and other diseases. Because introducing excess radiation into a living system can be harmful or, potentially, deadly, accurately determining the half-life of a radioisotope is critically-important. Therefore, the following sections of this chapter will describe the process for calculating the half-life of a radioisotope, and, subsequently, the resultant values will be applied to quantify the amount of a radioactive sample that has decayed in, or remains at, a specified period of time.
Calculating the Half-Life of a Radioisotope
The half-life of a radioisotope is a unique, experimentally-determined value that is calculated by comparing the relative masses of radioactive nuclei that are present in a sample at two different periods of time. While any mass unit can be used to measure the amount of radioactive material that is present a given sample, scientists primarily report mass-based data using milligrams, grams, or kilograms. Furthermore, as there is no restriction on the unit that can be used to express the amount of time that has elapsed in an experimental trial, chemists most often select the temporal unit that best complements the magnitude of the collected numerical data. As shown below in Table \(\PageIndex{1}\), the half-lives of radioactive isotopes can be as short as fractions of a second or as long as billions of years.
| Radioisotope | Half-Life |
|---|---|
| Carbon-16 | 747 milliseconds |
| Nobelium-254 | 57 seconds |
| Gallium-68 | 68 minutes |
| Fluorine-18 | 110 minutes |
| Plutonium-243 | 4.96 hours |
| Iodine-123 | 13.2 hours |
| Gold-198 | 2.7 days |
| Strontium-85 | 65 days |
| Carbon-14 | 5,730 years |
| Uranium-238 | 4.5 billion years |
Because, as stated above, the half-life of a radioisotope is determined by comparing relative experimental masses, the quantity of the initial radioactive sample that is being studied does not need to be carefully-controlled. However, since, by definition, exactly one-half of the initial amount must decay, in order to establish the half-life of a radioisotope, the remaining mass of the radioactive sample must be measured with a high degree of accuracy. If exactly one-half of a radioactive sample is allowed to decay in a particular experimental trial, the amount of time that has elapsed corresponds to the half-life of the radioisotope that is being studied. In contrast, if the amount of a given radioisotope that has decayed is not exactly equal to one-half of the initial value, the half-life of that isotope must be determined by applying a complex equation that relates the recorded masses using natural logarithms. Alternatively, if more than one-half of a radioactive sample has decayed in an experiment, the duration of the trial can be extended until the quantity of unstable nuclei that remains is exactly one-half of the amount that was present in the previous measurement. As shown in the following in-text problem and in Exercise \(\PageIndex{1}\), the half-life of a radioisotope can be calculated by equating the time that corresponds to the duration of the experimental trial to the number of half-lives that have elapsed in that time.
For example, calculate the half-life of chromium-51 if 78.75 grams of a 90.00-gram sample of this radioisotope decays in 84 days.
Because the half-life of a radioisotope is defined as the amount of time that is required for exactly one-half of a sample of that isotope to decay into more stable daughter nuclei, the initial quantity of chromium-51, 90.00 grams, must be halved, in order to determine the amount of this radioisotope that has decayed in the time that corresponds to one chromium-51 half-life. Since exactly one-half of a radioactive sample must decay during the period of time that equates to the half-life of a radioisotope, any numerical value that is calculated in, or applied to solve, a half-life problem should not be rounded.
Since a 90.00-gram sample of chromium-51 is initially present, half of this quantity, 45.00 grams, decays in the time that corresponds to one chromium-51 half-life, and, therefore, 45.00 grams of this radioisotope remains at that time. However, the given statement indicates that more than 45.00 grams of chromium-51 decays in 84 days. As a result, the decomposition of chromium-51 must be monitored for an extended period of time, until the amount of time that has elapsed equates to two total half-lives.
Because a 45.00-gram sample of chromium-51 is present at the beginning of the second half-life period, half of this quantity, 22.50 grams, decays in the time that corresponds to a second chromium-51 half-life, and, therefore, 22.50 grams of this radioisotope remains at that time. The total amount of chromium-51 that has decomposed in two half-lives, 67.50 grams, can be calculated by adding the amounts of chromium-51 that have decomposed, 45.00 grams and 22.50 grams, respectively, during each successive half-life. However, the given statement indicates that more than 67.50 grams of chromium-51 decays in 84 days. As a result, the decomposition of chromium-51 must be monitored for an extended period of time, until the amount of time that has elapsed equates to three total half-lives.
Since a 22.50-gram sample of chromium-51 is present at the start of the third half-life period, half of this quantity, 11.25 grams, decays in the time that corresponds to a third chromium-51 half-life, and, therefore, 11.25 grams of this radioisotope remains at that time. The total amount of chromium-51 that has decomposed in three half-lives, 78.75 grams, can be calculated by adding the amounts of chromium-51 that have decomposed, 45.00 grams, 22.50 grams, and 11.25 grams, respectively, during each successive half-life. Since the given statement indicates that exactly 78.75 grams of chromium-51 decays in 84 days, the decomposition of chromium-51 no longer needs to be be monitored.
The process of verbally summarizing the amount of chromium-51 that decays during and, therefore, that remains at the end of, each half-life is cumbersome and time-consuming. Furthermore, the quantitative information cannot be readily-interpreted in this format, due to the overwhelming amount of numerical data and words that are present. Therefore, summarizing these quantities using a symbolic format is more efficient, and the resultant data is more easily-understood, as shown below.

Finally, the half-life of chromium-51 is calculated by equating the time that corresponds to the duration of the experimental trial, 84 days, to the number of half-lives, 3, that have elapsed during that time, as shown below. As stated previously, because half-lives are exact quantities, the numerical answer that is calculated by simplifying this mathematical statement should not be rounded.
\({\rm{3t_{1/2}}}\) = \({\rm{84 \; d}}\)
\({\rm{t_{1/2}}}\) = \({\rm{28 \; d}}\)
Calculate the half-life of sodium-24 if 16.25 milligrams of a 260.00-milligram sample of this radioisotope remains after 60. hours has elapsed.
- Answer
- Because the half-life of a radioisotope is defined as the amount of time that is required for exactly one-half of a sample of that isotope to decay into more stable daughter nuclei, the initial quantity of sodium-24, 260.00 milligrams, must be halved, in order to determine the amount of this radioisotope that has decayed in the time that corresponds to one sodium-24 half-life. Since exactly one-half of a radioactive sample must decay during the period of time that equates to the half-life of a radioisotope, any numerical value that is calculated in, or applied to solve, a half-life problem should not be rounded.
Since a 260.00-milligram sample of sodium-24 is initially present, half of this quantity, 130.00 milligrams, decays in the time that corresponds to one sodium-24 half-life, and, therefore, 130.00 milligrams of this radioisotope remains at that time. However, the given statement indicates that less than 130.00 milligrams of sodium-24 remains after 60. hours has elapsed. As a result, the decomposition of this radioisotope must be monitored for an extended period of time, until the desired amount of sodium-24, 16.25 milligrams, remains. The amounts of sodium-24 that decay during, and remain at the end of, the time that corresponds to each successive sodium-24 half-life are symbolically-summarized below.
The half-life of sodium-24 is calculated by equating the time that corresponds to the duration of the experimental trial, 60. hours, to the number of half-lives, 4, that have elapsed during that time, as shown below. As stated previously, because half-lives are exact quantities, the numerical answer that is calculated by simplifying this mathematical statement should not be rounded.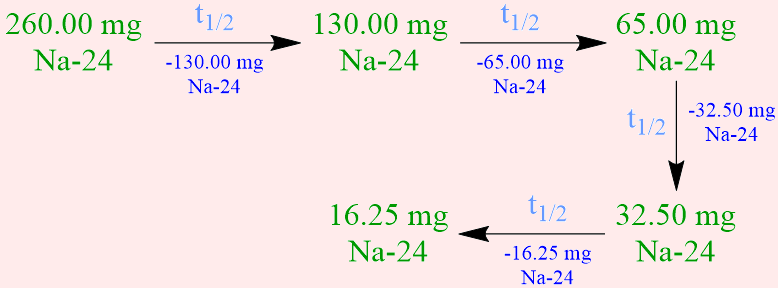
\({\rm{4t_{1/2}}}\) = \({\rm{60. \; h}}\)
\({\rm{t_{1/2}}}\) = \({\rm{15 \; h}}\)
Calculating Decayed and Remaining Radioactive Sample Quantities
If the half-life of a radioisotope is known, the process that is described above can be applied to determine the amount of a radioactive sample that has decayed in, or remains at, a specified period of time.
For example, calculate the amount of a 19.28-gram sample of radium-226 that has decayed in 3,200 years, if the the half-life of this radioisotope is 1,600 years.
Because the half-life of a radioisotope is defined as the amount of time that is required for exactly one-half of a sample of that isotope to decay into more stable daughter nuclei, the initial quantity of radium-226, 19.28 grams, must be halved, in order to determine the amount of this radioisotope that has decayed in 1,600 years, which is the time that corresponds to one radium-226 half-life. However, the given statement indicates that more than 1,600 years elapses during the corresponding experimental trial, and, consequently, the decomposition of this radioisotope must be monitored until the desired amount of time has passed. The amounts of radium-226 that decay during, and remain at the end of, each successive 1,600-year radium-226 half-life are symbolically-summarized below. Since exactly one-half of a radioactive sample must decay during the period of time that equates to the half-life of a radioisotope, any numerical value that is calculated in, or applied to solve, a half-life problem should not be rounded.
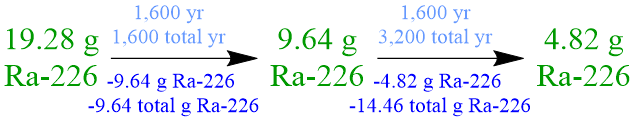
Based on this experimental data, 14.46 grams of radium-226 decays in the period of time that is specified in the given statement, 3,200 years, which is equivalent to two 1,600-year radium-226 half-lives.
Calculate the amount of a 880.0-milligram sample of oxygen-15 that remains after 10.35 minutes has elapsed, if the the half-life of this radioisotope is 2.07 minutes.
- Answer
- Because the half-life of a radioisotope is defined as the amount of time that is required for exactly one-half of a sample of that isotope to decay into more stable daughter nuclei, the initial quantity of oxygen-15, 880.0 milligrams, must be halved, in order to determine the amount of this radioisotope that has decayed in 2.07 minutes, which is the time that corresponds to one oxygen-15 half-life. However, the given statement indicates that more than 2.07 minutes elapses during the corresponding experimental trial, and, consequently, the decomposition of this radioisotope must be monitored until the desired amount of time has passed. The amounts of oxygen-15 that decay during, and remain at the end of, each successive 2.07-minute oxygen-15 half-life are symbolically-summarized below. Since exactly one-half of a radioactive sample must decay during the period of time that equates to the half-life of a radioisotope, any numerical value that is calculated in, or applied to solve, a half-life problem should not be rounded.
Based on this experimental data, 27.5 milligrams of oxygen-15 remains after the period of time that is specified in the given statement, 10.35 minutes, which is equivalent to five 2.07-minute oxygen-15 half-lives.

