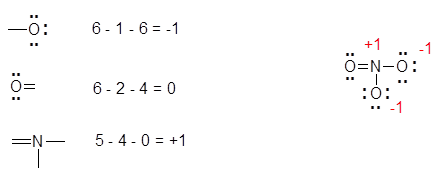Chemical bond refers to the forces holding atoms together to form molecules and solids. This force is of an electric nature, and the attraction between electrons of one atom to the nucleus of another atom contributes to what is known as chemical bonds. Various theories regarding chemical bonds have been proposed over the past 300 years, during which our interpretation of the world has also changed. Some old concepts such as Lewis dot structure and valency are still rather useful in our understanding of the chemical properties of atoms and molecules, and new concepts involving quantum mechanics of chemical bonding interpret modern observations very well. You learn new concepts such as bond length, bond energy, bond order, covalent bond, ionic bond, polar and non-polar bond etc. These concepts help you understand the material world at the molecular level.
Of the three primary theories of bonding discussed in this class (Lewis Theory, Valance Bond Theory and Molecular orbital theory), Lewis theory does not take full advantage of the quantum mechanical concepts discussed previously. Key to this theory is the Lewis Structure, which is a very simplified representation of the electrons in a molecule and is use to show how the electrons are arranged around individual atoms in a molecule. Between 1916 and 1919, Gilbert Newton Lewis, Walther Kossel, and Irving Langmuir formulated a theory to explain chemical bonding. This theory is now called Lewis Theory and it is based on the following five principles:
- Valence electrons, or the electrons in the outermost electron shell, have an essential role in chemical bonding.
- Ionic bonds are formed between atoms when electrons are transferred from one atom to another. Ionic bond is a bond between nonmetals and metals .
- Covalent bonds are formed between atoms when pairs of electrons are shared between atoms. A covalent bond is between two nonmetals.
- Electrons are transferred/shared so that each atom may reach a more stable electron configuration, i.e., the noble gas configuration which contains 8 valence electrons; this is called octet rule.
- Although many different Lewis structures can be constructed, those that are most stable have the lowest formal charge on the atoms.
Writing out Lewis structures can be at times, tricky and somewhat difficult. Moreover, a compound can have multiple Lewis Structures that contribute to the shape of the overall compound, so one Lewis structure of a compound may not necessarily be exactly what the compound looks like. If you need a refresher on how to constructing Lewis Structures consult the following Modules: Writing Lewis Structures, Lewis Structures I and Lewis Structures II.
In Lewis Structures, valence electrons are represented as dots and only outer-shell electrons are considered (e.g., the valence electrons and not the core electrons). Single (covalent) bonds are made up of two shared electrons and are represented by two dots between the bonded atoms or a single line. Double bonds and triple bonds are represented as two and three lines/(pairs of electrons), respectively. Lone pairs on the outer rims of an atom are represented as two dots. This is because they are the ones involved in chemical reactions. For the 2nd and 3rd periods elements, the number of valence electrons range from 1 to 8. Lewis dot structure for them are as indicated:
\[\mathrm{
\overset{\Large{.}}Li \hspace{20px}
\underset{\Large{.}}{\overset{\Large{.}}Be}\hspace{20px}
\cdot \overset{\Large{.}}{B} \cdot\hspace{20px}
\cdot \underset{\Large{.}}{\overset{\Large{.}}{C}} \cdot\hspace{20px}
\cdot \underset{\Large{.}}{\overset{\Large{.}}{N}} :\hspace{20px}
: \underset{\Large{.}}{\overset{\Large{.}}{O}} :\hspace{20px}
: \underset{\Large{.}}{\overset{\Large{..}}{F}} :\hspace{20px}
: \underset{\Large{..}}{\overset{\Large{..}}{Ne}} :}
\]
Lewis made the valence electron visible with dots. Other examples include the following molecules:
| \(\mathrm{H : H}\) |
\(\mathrm{H : \underset{\Large{..}}{\overset{\Large{..}}{O}} : H}\) |
\(\mathrm{H : \underset{\Large{..}}{\overset{\Large{..}}{F}} :}\) |
\(\mathrm{H : \underset{\Large{..}}{\overset{\Large{\underset{\huge{..}}H}}{N}} : H}\) |
\(\mathrm{H : \underset{\Large{\overset{\huge{..}}H}}{\overset{\Large{\underset{\huge{..}}H}}{C}} : H}\) |
\(\mathrm{: N ::: N :}\) |
\(\mathrm{: \overset{\Large{..}}O :: \overset{\Large{..}}O :}\) |
\(\mathrm{: \overset{\Large{..}}F : \overset{\Large{..}}F :}\) |
\(\mathrm{: \overset{\Large{..}}O :: C :: \overset{\Large{..}}O : }\) |
Note
Lewis structure does NOT attempt to explain the geometry of molecules, how the bonds form, or how the electrons are shared between the atoms. It is the simplest and most limited theory on electronic structure.
Principle 1: Valence Electrons
The electrons of an atom can divided into two categories: valence and core electrons. Valence electrons are those occupying the outermost shell or highest energy level of an atom while core electrons are those occupying the innermost shell or lowest energy level. This difference greatly influences the role of the two types of electrons in a chemical reaction. Generally, valence electrons can participate in the formation of chemical bonding, but core electrons cannot. While core electrons are not involved in bonding, they do have an influence on the chemical reactivity of an atom.
The electron configuration of the oxygen atoms is
\[O: \,1s^22s^22p^4 \label{1}\]
As discussed before, this configuration may be shorted
\[O:\, [He]2s^22p^4 \label{2}\]
where the \([He]\) stands for the configuration of helium (\(1s^22s^2\)). The \(1s\) electrons in oxygen (Equation \(\ref{1}\)) do not participate in bonding, i.e., chemistry, and are called core electrons. The other electrons (i.e., the \(2s^22p^4\) part) are call valence electrons and are responsible for the making and breaking of chemical bonds.
The configuration of calcium with 20 electrons can be written
\[Ca:\, [Ar]4s^2 \label{3}\]
where the \([Ar]\) stands for the configuration of argon (\(1s^22s^22p^63s^23p^6\)). Electronic configurations that are the same as noble gases are very stable since they have a full octet (except helium with a full 1s orbital). The electrons in the argon-like closed shell of Equation \(\ref{3}\) are the core electrons and the two electrons in the 4s orbital are valence electrons.
Example \(\PageIndex{1}\): Cobalt
What are the core and valence electrons in cobalt?
Solution
Start by writing the electron configuration of cobalt (i.e., 27 electrons):
\[1s^22s^22p^63s^23p^64s^23d^7 \nonumber\]
However, argon has the electronic structure \(1s^22s^22p^63s^23p^6\), so we can write the configuration of cobalt as
\[[Ar]4s^23d^7 \nonumber\]
The two electrons in the \(4s\) orbital and the seven electrons in the 3d are the valence electrons: all others are core electrons.
Principle 2: Ionic Bonding
In ionic bonding, electrons are transferred from one atom to another resulting in the formation of positive and negative ions. The electrostatic attractions between the positive and negative ions hold the compound together. The predicted overall energy of the ionic bonding process, which includes the ionization energy of the metal and electron affinity of the nonmetal, is usually positive, indicating that the reaction is endothermic and unfavorable. However, this reaction is highly favorable because of their electrostatic attraction.
The energy of the electrostatic attraction (\(E\)), a measure of the force’s strength, is inversely proportional to the internuclear distance between the charged particles (\(r\)):
\[ E = k\dfrac{Q_{1}Q_{2}}{r} \label{8.2.1b} \]
where each ion’s charge is represented by the symbol Q. The proportionality constant k is equal to 2.31 × 10−28 J·m.
Example \(\PageIndex{2}\): Ionic Bonding in NaCl
For example, in the reaction of Na (sodium) and Cl (chlorine), each Cl atom takes one electron from a Na atom. Therefore each Na becomes a Na+ cation and each Cl atom becomes a Cl- anion. Due to their opposite charges, they attract each other to form an ionic lattice. The formula (ratio of positive to negative ions) in the lattice is NaCl.
\[2Na_{(s)} + Cl_{2(g)} \rightarrow 2NaCl_{(s)} \nonumber\]
Sodium has one valence electron and chlorine has seven valence electrons; the two elements react such that the chlorine atom takes the valence electron from the sodium atom leaving the chlorine atom with one extra electron and thus negatively charged and the Sodium atom without an electron and thus positively charged. The two atoms then become ions and because of their opposite charges the ions are held together in an ionic bond (Equation \(\ref{8.2.1b}\)).
The chlorine has a high affinity for electrons, and the sodium has a low ionization potential. Thus the chlorine gains an electron from the sodium atom. The Lewis Structure of this reaction is (here we will consider one chlorine atom, rather than Cl2) is:
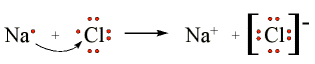
The arrow indicates the transfer of the electron from sodium to chlorine to form the Na+ metal ion and the Cl- chloride ion
Principle 3: Covalent Bonding
Covalent bonding occurs when pairs of electrons are shared by atoms. Atoms will covalently bond with other atoms in order to gain more stability, which is gained by forming a full electron shell. By sharing their outer most (valence) electrons, atoms can fill up their outer electron shell and gain stability. Nonmetals will readily form covalent bonds with other nonmetals in order to obtain stability, and can form anywhere between one to three covalent bonds with other nonmetals depending on how many valence electrons they posses. Although it is said that atoms share electrons when they form covalent bonds, they do not usually share the electrons equally.
The diatomic hydrogen molecule (H2) is the simplest model of a covalent bond, and is represented in Lewis structures as:
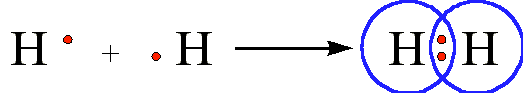
The shared pair of electrons provides each hydrogen atom with two electrons in its valence shell (the 1s) orbital. In a sense, it has the electron configuration of the noble gas helium. When two chlorine atoms covalently bond to form \(Cl_2Cl_2\), the following sharing of electrons occurs:
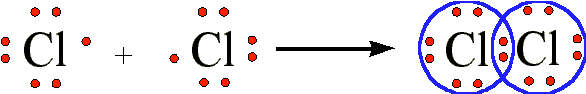
Each chlorine atom shared the bonding pair of electrons and achieves the electron configuration of the noble gas argon. In Lewis structures the bonding pair of electrons is usually displayed as a line, and the unshared electrons as dots:

The shared electrons are not located in a fixed position between the nuclei. In the case of the \(H_2H_2\) compound, the electron density is concentrated between the two nuclei:
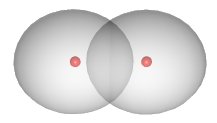
The two atoms are bound into the \(H_2H_2\) molecule mainly due to the attraction of the positively charged nuclei for the negatively charged electron cloud located between them.
Example \(\PageIndex{3}\): The Chlorate Ion
Draw the Lewis Structure for the chlorate ion (ClO3-).
Solution
First, lets find the how many valence electrons chlorate has:
ClO3- : 7 e-(from Cl) + 3(6) e-(from 3 O atoms) + 1 (from the total charge of -1) = 26
There are 26 valence electrons. Next lets draw the basic framework of the molecule:
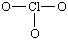
The molecule uses covalent bonds to hold together the atoms to the central Chlorine. The remaining electrons become non-bonding electrons. Since 6 electrons were used for the bonds, the 20 others become those un-bonding electrons to complete the octet:
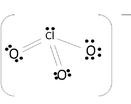
The oxygen atom's shells fill up with 18 electrons, and the other 2 complete Chlorine's octet
Example \(\PageIndex{4}\): Formaldehyde
Constructing the Lewis Structure of the formaldehyde (H2CO) molecule.
Solution
First find number of valence electrons:
H2CO: 2(1) e- (from the H atoms) + 4 e- (from the C atom) + 6 e- (from the O atom)
There are 12 valence electrons. Next draw out the framework of the molecule:
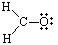
To satisfy the octet of Carbon, one of the pairs of electrons on Oxygen must be moved to create a double bond with Carbon. Therefore our Lewis Structure would look as it does below:
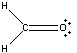
The Hydrogen atoms are each filled up with their two electrons and both the Carbon and the Oxygen atoms' octets are filled.
Principle 4: The Octet Rule
The octet rule is a chemical rule of thumb that reflects observation that atoms of main-group elements tend to combine in such a way that each atom has eight electrons in its valence shell, giving it the same electronic configuration as a noble gas. The Octet Rule requires all atoms in a molecule to have 8 valence electrons--either by sharing, losing or gaining electrons--to become stable. For covalent bonds, atoms to share their electrons with each other to satisfy the octet rule. It requires eight electrons because that is the amount of electrons needed to fill a s- and p- orbital (electron configuration); also known as a noble gas configuration. Although it is important to remember the "magic number" is 8, but there are many octet rule exceptions.
Octet Rule
A stable arrangement is attended when the atom is surrounded by eight electrons. This octet can be made up by own electrons and some electrons which are donated (e.g, ionic bonding) or shared (covalent bonding). An atom continues to form bonds until an octet of electrons is reached.
For the first rows in the periodic table, the magic number 8 can easily be explained from quantum mechanics of the multiple electron atoms discussed previously. In particular, electrons possess four quantum numbers (usually \(n\), \(l\), \(m_l\), and \(m_s\)), which are restricted as such:
\[ n = 1, 2, 3, ... \]
\[ l = 0, 1, 2, ..., n - 1 \]
\[ m_l = -l, -l + 1, ..., 0, ..., l - 1, l \]
\[ m_s = -\frac{1}{2}, \frac{1}{2} \]
where
- \(n\) is the principal quantum number (dealing with energy states),
- \(l\) is the orbital quantum number (dealing with subshells),
- \(m_l\) is the orbital magnetic quantum number (direction of \(l\)) and
- \(m_s\) is the spin quantum number (direction of spin).
By the Pauli's Exclusion Principle all of these numbers cannot be the same for any two electrons in an atom. So in the \(n = 2\) shell you can have two possible values for \(l\), one possible value for \(m_l\) when \(l = 0\), three possible values for \(m_l\) when \(l = 1\), and two possible values for \(m_s\). This sums to a total of eight possible value vectors:
\[(1 + 3) \cdot 2 = 8\]
In the \(n = 3\) shell, the Octet rule also holds for \(l < 2\), which gives you sort of the same combinatorics all over again.
Since the quantum numbers cannot be the same for any electrons in an atom, adding an extra electron to an atom with eight electrons in its outermost shell forces the electron to occupy an orbital with a higher principal quantum number (\(n\)). Since the binding energy of the electron increases with \(n\), this is energetically unfavorable to binding with an atom that has more space in its outermost shell. For example, for the nonmetals (and the 's' block metals) to achieve an octet, the number of valence electrons is equal to the group number (Table \(\PageIndex{1}\)).
Table \(\PageIndex{1}\): Select electronic properties of p-block elements of the 2nd row.
|
Element
|
Group
|
Valence electrons
|
Number of Covalent Bonds needed to form valence octet
|
|
F
|
17
|
7
|
1
|
|
O
|
16
|
6
|
2
|
|
N
|
15
|
5
|
3
|
|
C
|
14
|
4
|
4
|
Note: The 18 Electron Rule
The octet rule is not a law and it only works for a handful of elements, mainly the second-row p-block ones; there are many exceptions. Transition metals compounds often have 18 electrons on the metal atom because eighteen is the number of electrons in the nearest noble gas configuration in transition metals, which includes s + p + d electrons. The second and third row of transition metals have f electrons, too, but we usually simplify and don't worry about those electrons for electron counting purposes; we treat them like core electrons, not valence electrons.
Lewis theory successfully describe the covalent interactions between various nonmetal elements. Examples of hydride compounds of the elements in Table 12.2.1 (covalent compounds with hydrogen):
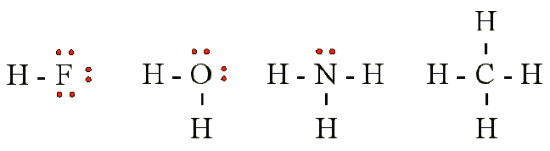
The sharing of a pair of electrons represents a single covalent bond, usually just referred to as a single bond. However, in many molecules atoms attain complete octets by sharing more than one pair of electrons between them.
- Two electron pairs shared a double bond
- Three electron pairs shared a triple bond

Because each nitrogen contains five valence electrons, they need to share three pairs to each achieve a valence octet. The strong nitrogen triple bond makes the molecule fairly inert. Moreover, the N - N bond distance in N2 is 1.10 Å, which is appreciably shorter than the average N-N single bonds (14.7Å).
It is sometimes possible to write more than one Lewis structure for a substance that does not violate the octet rule, as we saw for CH2O, but not every Lewis structure may be equally reasonable. In these situations, we can choose the most stable Lewis structure by considering the formal charge on the atoms, which is the difference between the number of valence electrons in the free atom and the number assigned to it in the Lewis electron structure. The formal charge is a way of computing the charge distribution within a Lewis structure; the sum of the formal charges on the atoms within a molecule or an ion must equal the overall charge on the molecule or ion. A formal charge does not represent a true charge on an atom in a covalent bond but is simply used to predict the most likely structure when a compound has more than one valid Lewis structure. To calculate formal charges, we assign electrons in the molecule to individual atoms according to these rules:
- Nonbonding electrons are assigned to the atom on which they are located.
- Bonding electrons are divided equally between the bonded atoms.
For each atom, we then compute a formal charge:
\[ \begin{matrix}
\text{formal charge}= & valence\; e^{-}- & \left ( nonbonding\; e^{-}+\dfrac{bonding\;e^{-}}{2} \right )\\
& ^{\left ( free\; atom \right )} & ^{\left ( atom\; in\; Lewis\; structure \right )}
\end{matrix} \label{8.5.1} \]
The most favorable Lewis Structure has the smallest formal charge for the atoms, and negative formal charges tend to come from more electronegative atoms. An example of determining formal charge can be seen below with the nitrate ion, NO3-:
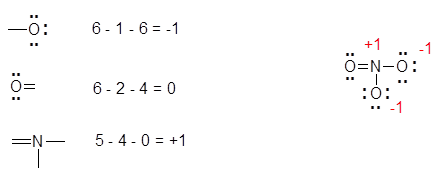
- The double bonded O atom has 6 electrons: 4 non-bonding and 2 bonding (one electron for each bond). Since O should have 6 electrons, the formal charge is 0.
- The two singly bonded O atoms each have 7 electrons: 6 non-bonding and 1 bonding electron. Since O should have 6 electrons, and there is one extra electron, those O atoms each have formal charges of -1.
- The N atom has 4 electrons: 4 bonding and 0 non-bonding electrons. Since N should have 5 electrons and there are only 4 electrons for this N, the N atom has a formal charge of +1.
- The charges add up to the overall charge of the ion. 0 + (-1) + (-1) + 1 = -1. Thus, these charges are correct, as the overall charge of nitrate is -1.
In general you want the fewest number of formal charges possible, i.e. formal charges of 0 for as many of the atoms in a structure as possible. Also the formal charges should match the electronegativity of the atom, that is negative charges should be on the more electronegative atoms and positive charges on the least electronegative atoms if possible. Charges of -1 and +1 on adjacent atoms can usually be removed by using a lone pair of electrons from the -1 atom to form a double (or triple) bond to the atom with the +1 charge.
Summary
Lewis Structures are visual representations of the bonds between atoms and illustrate the lone pairs of electrons in molecules. They can also be called Lewis dot diagrams and are used as a simple way to show the configuration of atoms within a molecule. Electrons are shown as "dots" or for bonding electrons as a line between the two atoms. The goal is to obtain the "best" electron configuration, i.e. the octet rule and formal charges need to be satisfied. Lewis structures can also be useful in predicting molecular geometry in conjunction with hybrid orbitals. A compound may have multiple resonance forms that are also all correct Lewis structures. This section will discuss the rules for writing out Lewis structures correctly.
Contributors and Attributions