4.4 Shapes of Molecules - VSEPR Theory and Valence Bond Theory
- Page ID
- 218257
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)VSEPR Theory
Valence Shell Electron Pair Repulsion Theory uses the basic idea that electron pairs are mutually repulsed to predict the arrangement of electron pairs around a central atom (an atom that has at least two other atoms bonded directly to it). The key to correctly applying VSEPR Theory is to start with a correct Lewis dot structure. From a correct Lewis dot structure, it is a straightforward process to determine the shape of a molecule or polyatomic ion by determining the arrangement of electron pairs around every central atom in the molecule or polyatomic ion.
The step-by-step process to determine the shape around each central atom is
1. Draw the Lewis dot structure.
2. Apply the following analysis to each separate, central atom (where a central atom is an atom with two or more other atoms bonded directly to it.)
a) Find the number of "things attached" to the central atom, where a "thing attached" is either an atom or a non-bonding electron pair.
(Actually, you are counting the number of hybrid orbitals on the central atom, but that is the next theory to be discussed.)
It is important to remember that you are not counting bonds!
b) Find the Electron Pair Arrangement (EPA) in the table below
| # of Things Attached | Electron Pair Arrangement | Ideal Bond Angle |
|---|---|---|
| 2 | line (linear shape) | 180 |
| 3 | trigonal plane( trigonal planar shape) | 120 |
| 4 | tetrahedron (tetrahedral shape) | 109.5 |
c) Find the Molecular Geometry (MG) of the particle, determined by counting up the number of atoms and the number of lone pairs and using this table:
| # of atoms attached | # of lone pairs attached | Electron Pair Arrangement | Molecular Geometry | Bond angle | Example |
|---|---|---|---|---|---|
| 2 | 0 | line | line | 180 | CO2 |
| 3 | 0 | trigonal plane | trigonal plane | 120 | BF3 |
| 2 | 1 | trigonal plane | bent | <120 | SO2 |
| 4 | 0 | tetrahedron | tetrahedron | 109.5 | CH4 |
| 3 | 1 | tetrahedron | trigonal pyramid | <109.5 | NH3 |
| 2 | 2 | tetrahedron | bent | <109.5 | H2O |
Example \(\PageIndex{1}\)
Determine the Electron Pair Arrangement and Molecular Geometry about the central atom(s) in a) OF2 and b) CH3CN.
Solution
a) The Lewis dot structure of OF2 is 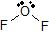 (leaving off the lone pairs on the non-central F atoms.)
(leaving off the lone pairs on the non-central F atoms.)
There are 2 atoms and 2 lone pairs attached to the central O atom, for a total of 4 "things attached."
From the two tables above, we can see that the O atom must have an EPA of a tetrahedron, and its MG is bent.
b) The Lewis dot structure of CH3CN is
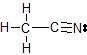
There are 4 atoms and 0 lone pairs attached to the central C atom on the left, for a total of 4 "things attached."
From the two tables above, we can see that this C atom must have an EPA of a tetrahedron, and its MG is also a tetrahedron.
There are 2 atoms and 0 lone pairs attached to the central C atom on the right, for a total of 2 "things attached."
From the two tables above, we can see that this C atom must have an EPA of a line, and its MG is also a line.
Exercise \(\PageIndex{1}\)
Determine the Electron Pair Arrangement and Molecular Geometry about the central atom(s) in a) PF3 and b) CH2NH.
- Answer
-
a) The Lewis dot structure of PF3 is
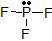 (leaving off the lone pairs on the non-central F atoms.)
(leaving off the lone pairs on the non-central F atoms.)There are 3 atoms and 1 lone pair attached to the central P atom, for a total of 4 "things attached."
From the two tables above, we can see that the P atom must have an EPA of a tetrahedron, and its MG is a trigonal pyramid.
b)The Lewis dot structure of CH2NH is
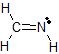
There are 3 atoms and 0 lone pairs attached to the central C atom on the left, for a total of 3 "things attached."
From the two tables above, we can see that this C atom must have an EPA of a trigonal plane, and its MG is also a trigonal plane.
There are 2 atoms and 1 lone pair attached to the central N atom on the right, for a total of 3 "things attached."
From the two tables above, we can see that this N atom must have an EPA of a trigonal plane, and its MG is bent.
Example \(\PageIndex{1}\)
Use the VSEPR model to predict the number of atoms and lone pairs attached, the electron pair arrangement, and molecular geometry of the central atom in each compound.
- H2S
- CHCl3
Given: two chemical compounds
Asked for: number of atoms and lone pairs attached, the electron pair arrangement and molecular geometry
Strategy:
- Using the VSEPR approach to determine the number of atoms and lone pairs attached, the electron pair arrangement, and the molecular geometry of the central atom in each molecule.
Solution:
a. H2S has two atoms and two lone pairs attached to the sulfur atom, so the VSEPR model predicts an electron pair arrangement of a tetrahedron and a molecular geometry that is bent, or V shaped.
b. The central C atom in the CHCl3 molecule has four atoms attached and no lone pairs. The carbon atom has an electron pair arrangement of a tetrahedron, and the molecular geometry is a tetrahedral shape.
Exercise \(\PageIndex{1}\)
Use the VSEPR model to predict the number of atoms and lone pairs attached, the electron pair arrangement, and molecular geometry for the central atom(s) in each compound. and then describe the hybridization and bonding of all atoms except hydrogen.
a. the BF4− ion
b. hydrazine (H2N–NH2)
- Answer a
-
B has four atoms attached and no lone pairs, so it forms an electron pair arrangement of a tetrahedron. The molecular geometry is tetrahedral shape.
- Answer b
-
Each N atom has three other atoms attached and one lone pair attached. The electron pair arrangement is a tetrahedron. The molecular geometry about each N is a trigonal pyramidal shape.

