Skip to main content
Chemistry LibreTexts

3.9: End of Chapter Problems

  1. Last updated
  2. Save as PDF
  • Page ID
    366141

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    1. Explain why the symbol for an atom of the element oxygen and the formula for a molecule of oxygen differ.
    2. Explain why the symbol for the element sulfur and the formula for a molecule of sulfur differ.
    3. Write the molecular and empirical formulas of the following compounds:

    Figure A shows a carbon atom that forms two, separate double bonds with two oxygen atoms.

    Figure B shows a hydrogen atom which forms a single bond with a carbon atom. The carbon atom forms a triple bond with another carbon atom. The second carbon atom forms a single bond with a hydrogen atom.

    Figure C shows a carbon atom forming a double bond with another carbon atom. Each carbon atom forms a single bond with two hydrogen atoms.

    Figure D shows a sulfur atom forming single bonds with four oxygen atoms. Two of the oxygen atoms form a single bond with a hydrogen atom.

    Answer
    a. molecular CO2, empirical CO2; b. molecular C2H2, empirical CH; c. molecular C2H4, empirical CH2; d. molecular H2SO4, empirical H2SO4
    1. Write the molecular and empirical formulas of the following compounds:

    Figure A shows a structural diagram of four carbon atoms bonded together into a chain. The two carbon atoms on the left form a double bond with each other. All of the remaining carbon atoms form single bonds with each other. The leftmost carbon also forms single bonds with two hydrogen. The second carbon in the chain forms a single bond with a hydrogen atom. The third carbon in the chain forms a single bond with two hydrogen atoms each. The rightmost carbon forms a single bond with three hydrogen atoms each.

    Figure B shows a structural diagram of a molecule that has a chain of four carbon atoms. The leftmost carbon atom forms a single bond with three hydrogen atoms each and single bond with the second carbon atom. The second carbon atom forms a triple bond with the third carbon atom. The third carbon atom forms a single bond to the fourth carbon atom. The fourth carbon atom forms a single bond to three hydrogen atoms each.

    Figure C shows a structural diagram of two silicon atoms are bonded together with a single bond. Each of the silicon atoms form single bonds to two chlorine atoms each and one hydrogen atom.

    Figure D shows a structural diagram of a phosphorus atom that forms a single bond to four oxygen atoms each. Three of the oxygen atoms each have a single bond to a hydrogen atom.

    1. Determine the empirical formulas for the following compounds:
    1. caffeine, C8H10N4O2
    2. fructose, C12H22O11
    3. hydrogen peroxide, H2O2
    4. glucose, C6H12O6
    5. ascorbic acid (vitamin C), C6H8O6
    Answer
    a. C4H5N2O; b. C12H22O11; c. HO; d. CH2O; e. C3H4O3
    1. Determine the empirical formulas for the following compounds:
    1. acetic acid, C2H4O2
    2. citric acid, C6H8O7
    3. hydrazine, N2H4
    4. nicotine, C10H14N2
    5. butane, C4H10
    1. Write the empirical formulas for the following compounds:

    Figure A shows a structural diagram of two carbon atoms that form a single bond with each other. The left carbon atom forms single bonds with hydrogen atoms each. The right carbon forms a double bond to an oxygen atom. The right carbon also forms a single bonded to another oxygen atom. This oxygen atom also forms a single bond to a hydrogen atom.

    Figure B shows a structural diagram containing a leftmost carbon that forms single bonds to three hydrogen atoms each. This leftmost carbon also forms a single bond to a second carbon atom. The second carbon atom forms a double bond with an oxygen atom. The second carbon also forms a single bond to a second oxygen atom. This oxygen atom forms a single bond to a third carbon atom. This third carbon atom forms single bonds with two hydrogen atoms each as well as a single bond with another carbon atom. The rightmost carbon atom forms a single bond with three hydrogen atoms each.

    Answer
    a. CH2O; b. C2H4O
    1. Open the Build a Molecule simulation and select the “Larger Molecules” tab. Select an appropriate atoms “Kit” to build a molecule with two carbon and six hydrogen atoms. Drag atoms into the space above the “Kit” to make a molecule. A name will appear when you have made an actual molecule that exists (even if it is not the one you want). You can use the scissors tool to separate atoms if you would like to change the connections. Click on “3D” to see the molecule, and look at both the space-filling and ball-and-stick possibilities.
    1. Draw the structural formula of this molecule and state its name.
    2. Can you arrange these atoms in any way to make a different compound?
    1. Use the Build a Molecule simulation to repeat Exercise, but build a molecule with two carbons, six hydrogens, and one oxygen.
    1. Draw the structural formula of this molecule and state its name.
    2. Can you arrange these atoms to make a different molecule? If so, draw its structural formula and state its name.
    3. How are the molecules drawn in (a) and (b) the same? How do they differ? What are they called (the type of relationship between these molecules, not their names).
    Answer

    a. ethanol

    A Lewis Structure is shown. An oxygen atom is bonded to a hydrogen atom and a carbon atom. The carbon atom is bonded to two hydrogen atoms and another carbon atom. That carbon atom is bonded to three more hydrogen atoms. There are a total of two carbon atoms, six hydrogen atoms, and one oxygen atoms.

    b. methoxymethane, more commonly known as dimethyl ether

    A Lewis Structure is shown. An oxygen atom is bonded to two carbon atoms. Each carbon atom is bonded to three different hydrogen atoms. There are a total of two carbon atoms, six hydrogen atoms, and one oxygen atom.

    c. These molecules have the same chemical composition (types and number of atoms) but different chemical structures. They are structural isomers.1

    1. Use the Build a Molecule simulation to repeat Exercise, but build a molecule with three carbons, seven hydrogens, and one chlorine.
    1. Draw the structural formula of this molecule and state its name.
    2. Can you arrange these atoms to make a different molecule? If so, draw its structural formula and state its name.
    3. How are the molecules drawn in (a) and (b) the same? How do they differ? What are they called (the type of relationship between these molecules, not their names)?
    1. Using the periodic table, predict whether the following chlorides are ionic or covalent: KCl, NCl3, ICl, MgCl2, PCl5, and CCl4.
    Answer
    Ionic: KCl, MgCl2; Covalent: NCl3, ICl, PCl5, CCl415. (a) CaS; (b) (NH4)2CO3; (c) AlBr3; (d) Na2HPO4; (e) Mg3 (PO4)2
    1. Using the periodic table, predict whether the following chlorides are ionic or covalent: SiCl4, PCl3, CaCl2, CsCl, CuCl2, and CrCl3.
    2. For each of the following compounds, state whether it is ionic or covalent. If it is ionic, write the symbols for the ions involved:
    1. NF3
    2. BaO,
    3. (NH4)2CO3
    4. Sr(H2PO4)2
    5. IBr
    6. Na2O
    Answer
    a. covalent; b. ionic, Ba2+, O2−; c. ionic, \(\ce{NH4+}\), \(\ce{CO3^2-}\); d. ionic, Sr2+, \(\ce{H2PO4-}\); e. covalent; f. ionic, Na+, O2−
    1. For each of the following compounds, state whether it is ionic or covalent, and if it is ionic, write the symbols for the ions involved:
    1. KClO4
    2. MgC2H3O2
    3. H2S
    4. Ag2S
    5. N2Cl4
    6. Co(NO3)2
    1. For each of the following pairs of ions, write the symbol for the formula of the compound they will form:
    1. Ca2+, S2−
    2. \(\ce{NH4+}\), \(\ce{SO4^2-}\)
    3. Al3+, Br−
    4. Na+, \(\ce{HPO4^2-}\)
    5. Mg2+, \(\ce{PO4^3-}\)
    1. For each of the following pairs of ions, write the symbol for the formula of the compound they will form:
    1. K+, O2−
    2. \(\ce{NH4+}\), \(\ce{PO4^3-}\)
    3. Al3+, O2−
    4. Na+, \(\ce{CO3^2-}\)
    5. Ba2+, \(\ce{PO4^3-}\)
    1. Name the following compounds:
    1. CsCl
    2. BaO
    3. K2S
    4. BeCl2
    5. HBr
    6. AlF3
    Answer
    a. cesium chloride; b. barium oxide; c. potassium sulfide; d. beryllium chloride; e. hydrogen bromide; f. aluminum fluoride
    1. Name the following compounds:
    1. NaF
    2. Rb2O
    3. BCl3
    4. H2Se
    5. P4O6
    6. ICl3
    1. Write the formulas of the following compounds:
    1. rubidium bromide
    2. magnesium selenide
    3. sodium oxide
    4. calcium chloride
    5. hydrogen fluoride
    6. gallium phosphide
    7. aluminum bromide
    8. ammonium sulfate
    Answer
    a. RbBr; b. MgSe; c. Na2O; d. CaCl2; e. HF; f. GaP; g. AlBr3; h. (NH4)2SO4
    1. Write the formulas of the following compounds:
    1. lithium carbonate
    2. sodium perchlorate
    3. barium hydroxide
    4. ammonium carbonate
    5. sulfuric acid
    6. calcium acetate
    7. magnesium phosphate
    8. sodium sulfite
    1. Write the formulas of the following compounds:
    1. chlorine dioxide
    2. dinitrogen tetraoxide
    3. potassium phosphide
    4. silver(I) sulfide
    5. aluminum nitride
    6. silicon dioxide
    Answer
    a. ClO2; b. N2O4; c. K3P; d. Ag2S; e. AlN; f. SiO2
    1. Write the formulas of the following compounds:
    1. barium chloride
    2. magnesium nitride
    3. sulfur dioxide
    4. nitrogen trichloride
    5. dinitrogen trioxide
    6. tin(IV) chloride
    1. Each of the following compounds contains a metal that can exhibit more than one ionic charge. Name these compounds:
    1. Cr2O3
    2. FeCl2
    3. CrO3
    4. TiCl4
    5. CoO
    6. MoS2
    Answer
    a. chromium(III) oxide; b. iron(II) chloride; c. chromium(VI) oxide; d. titanium(IV) chloride; e. cobalt(II) oxide; f. molybdenum(IV) sulfide
    1. Each of the following compounds contains a metal that can exhibit more than one ionic charge. Name these compounds:
    1. NiCO3
    2. MoO3
    3. Co(NO3)2
    4. V2O5
    5. MnO2
    6. Fe2O3
    1. The following ionic compounds are found in common household products. Write the formulas for each compound:
    1. potassium phosphate
    2. copper(II) sulfate
    3. calcium chloride
    4. titanium dioxide
    5. ammonium nitrate
    6. sodium bisulfate (the common name for sodium hydrogen sulfate)
    Answer
    a. K3PO4; b. CuSO4; c. CaCl2; d. TiO2; e. NH4NO3; f. NaHSO4
    1. The following ionic compounds are found in common household products. Name each of the compounds:
    1. Ca(H2PO4)2
    2. FeSO4
    3. CaCO3
    4. MgO
    5. NaNO2
    6. KI
    1. What are the IUPAC names of the following compounds?
    1. manganese dioxide
    2. mercurous chloride (Hg2Cl2)
    3. ferric nitrate [Fe(NO3)3]
    4. titanium tetrachloride
    5. cupric bromide (CuBr2)
    Answer
    a. manganese(IV) oxide; b. mercury(I) chloride; c. iron(III) nitrate; d. titanium(IV) chloride; e. copper(II) bromide
    1. Find the amount of moles contained in each specimen.
    1. 7.87 kg H2O2
    2. 2.34 kg NaCl
    3. 12.5 g C2H6O
    4. 85.72 g NH3
    Answer

    A. First, determine the units that are given for each sample. In order to convert these measurements to moles, each sample should first be written in grams. Two of the given samples are measured in kilograms. Use the following conversion factor to convert kilograms to grams, with \(x\) representing the given mass:

    \[x\, kg\cdot \dfrac{1000\, g}{1\, kg}\]

    B. Next, find the atomic masses of all the atoms in each compound by using the Periodic Table. Then, add these atomic masses together for each compound. The resulting value will be the number of grams of each sample that make up one mole.

    C. Convert the mass in grams of each sample to moles by multiplying it by the following conversion factor, called the molar mass, with x representing the mass of the given specimen and \(y\) representing the calculated atomic mass found in step B:

    \[x\, g\cdot \dfrac{1\, mole}{y\, g}\]

    A Numbers 1 and 2 first need to be converted into grams.

    a. \[7.87\, kg\, H_2O_2\cdot \dfrac{1000\, g}{1\, kg}=7,870\, g\, H_2O_2\]

    b. \[2.34\, kg\, NaCl\cdot \dfrac{1000\, g}{1\, kg}=2,340\, g\, NaCl\]

    B The following are the calculated molar masses of each of the given compounds. The atomic mass of each element has been rounded to 4 significant figures in these calculations.

    a. H2O2: \[2\, (1.008\, g\, H)+2\, (16.00\, g\, O)=\dfrac{34.02\, g}{1\, mole}\, H_2O_2\]

    b. NaCl: \[(22.99\, g\, Na)+(35.45\, g\, Cl)=\dfrac{58.44\, g}{1\, mole}\, NaCl\]

    c. C2H6O: \[2\, (12.01\, g\, C)+6\, (1.008\, g\, H)+\left ( 16.00\, g\, O \right )=\dfrac{46.07\, g}{1\, mole}\, C_2H_6O\]

    d. NH3: \[(14.01\, g\, N)+3\, (1.008\, g\, H)=\dfrac{17.03\, g}{1\, mole}\, NH_3\]

    C The number of moles in each specimen can now be calculated by multiplying the mass in grams of each sample by its molarity.

    a. \[7,870\, g\, H_2O_2\cdot \dfrac{1\, mole\, H_2O_2}{34.02\, g\, H_2O_2}=231\, moles\, H_2O_2\]

    b. \[2,340\, g\, NaCl\cdot \dfrac{1\, mole\, NaCl}{58.44\, g\, NaCl}=40.0\, moles\, NaCl\]

    c. \[12.5\, g\, C_2H_6O\cdot \dfrac{1\, mole\, C_2H_6O}{46.07\, g\, C_2H_6O}=0.271\, moles\, C_2H_6O\]

    d. \[85.72\, g\, NH_3\cdot \dfrac{1\, mole\, NH_3}{17.03\, g\, NH_3}=5.033\, moles\, NH_3\]

    1. Calculate the number of moles in each of the following examples.
    1. 402.5 mg of NO2
    2. 2.7 kg of H2O
    3. 323 g of CBr4
    4. 2.9 kg of CaO
    Answer

    a) First, calculate the molar mass of NO2.

    14.007g/mol N + 2 (15.999 g/mol O) = 46.0055 g/mol

    Now, convert the sample from mg to g.

    402.5 mg NO2 1 g 0.4025 g NO2
      1000 mg  

    Finally, use the molar mass to determine how many moles your sample size contains.

    0.4025 g NO2 1 mol 0.0087 moles of NO2
      46.0055 g  

    This gives us the final answer, 0.0087 moles of NO2.

    From this, we can deduce that:

    \[\text{Moles of substance} = \text{Mass of substance (g)}{Molar mass of substance}\]

    b) 150 moles of H2O

    c) 0.974 moles of CBr4

    d) 52 moles of CaO

    1. For each substance, convert the given molecules to mass in grams:
    1. 3.2 x 1024 Cl2 molecules
    2. 8.25 x 1018 CH2O molecules
    3. 1 carbon dioxide molecule
    Answer

    Step 1: Convert the given molecules to moles by dividing by Avogadro's number.

    Step 2: Multiply the number of moles by the Molar Mass of the substance to determine the grams.

    Step 3: Through correct Dimensional Analysis, the molecules and moles will cancel to leave grams.

    \[\dfrac{molecules}{Avogadro's}\rightarrow moles\rightarrow moles \cdot MM\rightarrow grams\]

    Helpful Hints:

    Avogadro's number: 6.022 x 1023 mol of a substance Molar mass (MM): the weight of a substance in the units g/mol, found by adding the atomic masses of each element.
    • Example: MM of H2O --> H(1.008 x 2) + O(15.999)= 18 g/mol

    c) 7.31 x 1025 grams

    Solution

    a) 3.8 x 1051 grams

    b) 4.11 x 1045 grams

    1. Write the empirical formula and molecular formula for the compound with the given percent composition and molecular weight.
    • 40.0% Carbon
    • 6.70% Hydrogen
    • 53.3% Oxygen

    Molecular Weight ≈ 240 g/mol

    Answer

    Calculate amount of grams of each element we have. Convert amount of grams into number of moles of each element. Obtain molecular formula. Find the common factor among the number of atoms each elements has, then obtain the empirical formula.

    Solution:

    1. Calculate amount of grams in each element:

    CodeCogsEqn.gif

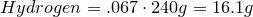
    CodeCogsEqn-2.gif

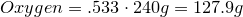
    CodeCogsEqn-3.gif

    2. Convert amount of grams into number of moles of each elements:

    Carbon-

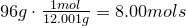
    CodeCogsEqn-4.gif

    Hydrogen-

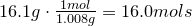
    CodeCogsEqn-5.gif

    Oxygen-

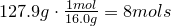
    CodeCogsEqn-6.gif

    3. Obtain molecular formula:

    \[C_8H_{16}O_8\]

    4. Find common factor and obtain empirical formula:

    Common factor is 8

    Empirical formula is

    \[CH_2O\]

    1. For several compounds both the molar mass and and empirical formulas are listed. What is the molecular formula for each compound.
    1. C2OH4, 88 g/mol
    2. C2H8N, 46 g/mol
    3. NH2, 32 g/mol
    Answer

    Find the empirical formula mass of the compound B. Determine the ratio between the empirical formula mass and the molar mass of the compound C.Multiply the empirical formula by the factor found in part B.

    Solution:

    C2OH4, 88 g/mol

    A.

    Carbon: 2(12.0g/mol)

    Oxygen: 1(16.0g/mol)

    Hydrogen: 4(1.0g/mol)

    =44.0 g/mol

    B.

    \[\dfrac{88.0g/mol}{44.0g/mol}=2\]

    C.

    2(C2OH4)= C4O2H8

    C2H8N, 46 g/mol

    A.

    Carbon: 2(12.0g/mol)

    Hydrogen: 8(1.0g/mol)

    Nitrogen: 1(14.0g/mol)

    =46.0 g/mol

    B.

    \[\dfrac{46.0g/mol}{46.0g/mol}=1.0\]

    C.

    1(C2H8N)=C2H8N

    NH2

    A.

    Nitrogen: 1(14.0g/mol)

    Hydrogen: 2(1.0g/mol)

    =16.0g/mol

    B.

    \[\dfrac{32.0g/mol}{16.0g/mol}=2\]

    C.

    2(NH2)=N2H4

    1. After the combustion of a hydrocarbon, we find 66.02g of CO2 and 27.02g of H2O. What is the empirical formula of this hydrocarbon?
    Answer

    66.02 x 1 mol/ 44.0 g= 1.500 mol CO2= 1.5 mol C

    27.02 x 1 mol/ 18g = 1.501 mol H20= 3 mol H

    C1.5 H3= C3 H6

    You start by taking both, divide by the molar mass, use the mol ratio of the compound and multiple to get rid of decimals.

    Additional Question

    Additional Questions 1. For the following molecules; write the chemical formula, determine how many atoms are present in one molecule, determine the molecular weight, determine the number of moles in exactly 1 gram, and the number of moles in exactly 10-6 gram. a. carbon dioxide b. iron (II) chloride c. dinitrogen pentoxide d. iron (III) sulfate 2. Name the following compounds, determine the molecular weight, determine the percent composition, and determine how many moles in 8.35 grams of the compound. a. KI b. CaF2 c. Cu2SO4 d. N2O e. LiOH 3. Give the chemical formula (or atomic symbol), molecular (or atomic) weight, and charge for the following ions: a. sulfate b. sulfite c. nitrate d. chloride e. nitride f. acetate g. carbonate 4. Calculate the number of moles in: a. 20.1797 g of Ne b. 45.3594 g of Ne c. 0.198669 g of Ne 5. Calculate the mass of: a. 2.00 mole of Fe b. 4.362 x 10-5 mol of Fe c. 4.362 x 10-5 mol of Li

    3.9: End of Chapter Problems is shared under a not declared license and was authored, remixed, and/or curated by LibreTexts.

    1. Back to top
    • Was this article helpful?

    Recommended articles

    1. Article type
      Section or Page
    2. Tags
      This page has no tags.