3.8: Determine Empirical Formula from Combustion Analysis

Last updated
Save as PDF

Page ID: 366140

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Learning Objectives

Determine the empirical formula of a compound using combustion analysis.

When a compound containing carbon and hydrogen is subject to combustion with oxygen in a special combustion apparatus all the carbon is converted to CO₂ and the hydrogen to H₂O (Figure \(\PageIndex{1}\)). The amount of carbon produced can be determined by measuring the amount of CO₂ produced. This is trapped by the sodium hydroxide, and thus we can monitor the mass of CO₂ produced by determining the increase in mass of the CO₂ trap. Likewise, we can determine the amount of H produced by the amount of H₂O trapped by the magnesium perchlorate.

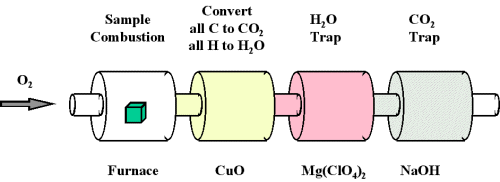
4 cylinders connected to each other to show the phases involved in combustion analysis.

Figure \(\PageIndex{1}\): Combustion analysis apparatus

One of the most common ways to determine the elemental composition of an unknown hydrocarbon is an analytical procedure called combustion analysis. A small, carefully weighed sample of an unknown compound that may contain carbon, hydrogen, nitrogen, and/or sulfur is burned in an oxygen atmosphere,Other elements, such as metals, can be determined by other methods. and the quantities of the resulting gaseous products (CO₂, H₂O, N₂, and SO₂, respectively) are determined by one of several possible methods. One procedure used in combustion analysis is outlined schematically in Figure \(\PageIndex{2}\) and a typical combustion analysis is illustrated in Examples \(\PageIndex{1}\) and \(\PageIndex{2}\).

Figure \(\PageIndex{2}\): Steps for Obtaining an Empirical Formula from Combustion Analysis

Example \(\PageIndex{1}\): Combustion of Isopropyl Alcohol

What is the empirical formulate for isopropyl alcohol (which contains only C, H and O) if the combustion of a 0.255 grams isopropyl alcohol sample produces 0.561 grams of CO₂ and 0.306 grams of H₂O?

Solution

From this information quantitate the amount of C and H in the sample.

\[ (0.561\; \cancel{g\; CO_2}) \left( \dfrac{1 \;mol\; CO_2}{44.0\; \cancel{g\;CO_2}}\right)=0.0128\; mol \; CO_2 \]

Since one mole of CO₂ is made up of one mole of C and two moles of O, if we have 0.0128 moles of CO₂ in our sample, then we know we have 0.0128 moles of C in the sample. How many grams of C is this?

\[ (0.0128 \; \cancel{mol\; C}) \left( \dfrac{12.011\; g \; C}{1\; \cancel{mol\;C}}\right)=0.154\; g \; C \]

How about the hydrogen?

\[ (0.306 \; \cancel{g\; H_2O}) \left( \dfrac{1\; mol \; H_2O}{18.0\; \cancel{g \;H_2O}}\right)=0.017\; mol \; H_2O \]

Since one mole of H₂O is made up of one mole of oxygen and two moles of hydrogen, if we have 0.017 moles of H₂O, then we have 2*(0.017) = 0.034 moles of hydrogen. Since hydrogen is about 1 gram/mole, we must have 0.034 grams of hydrogen in our original sample.

When we add our carbon and hydrogen together we get:

0.154 grams (C) + 0.034 grams (H) = 0.188 grams

But we know we combusted 0.255 grams of isopropyl alcohol. The 'missing' mass must be from the oxygen atoms in the isopropyl alcohol:

0.255 grams - 0.188 grams = 0.067 grams oxygen

This much oxygen is how many moles?

\[ (0.067 \; \cancel{g\; O}) \left( \dfrac{1\; mol \; O}{15.994\; \cancel{g \;O}}\right)=0.0042\; mol \; O \]

Overall therefore, we have:

0.0128 moles Carbon
0.0340 moles Hydrogen
0.0042 moles Oxygen

Divide by the smallest molar amount to normalize:

C = 3.05 atoms
H = 8.1 atoms
O = 1 atom

Within experimental error, the most likely empirical formula for propanol would be \(C_3H_8O\)

Example \(\PageIndex{2}\): Combustion of Naphalene

Naphthalene, the active ingredient in one variety of mothballs, is an organic compound that contains carbon and hydrogen only. Complete combustion of a 20.10 mg sample of naphthalene in oxygen yielded 69.00 mg of CO₂ and 11.30 mg of H₂O. Determine the empirical formula of naphthalene.

Given: mass of sample and mass of combustion products

Asked for: empirical formula

Strategy:

Use the masses and molar masses of the combustion products, CO₂ and H₂O, to calculate the masses of carbon and hydrogen present in the original sample of naphthalene.
Use those masses and the molar masses of the elements to calculate the empirical formula of naphthalene.

Solution:

A Upon combustion, 1 mol of CO2 is produced for each mole of carbon atoms in the original sample. Similarly, 1 mol of H₂O is produced for every 2 mol of hydrogen atoms present in the sample. The masses of carbon and hydrogen in the original sample can be calculated from these ratios, the masses of CO₂ and H₂O, and their molar masses. Because the units of molar mass are grams per mole, we must first convert the masses from milligrams to grams:

\[ mass \, of \, C = 69.00 \, mg \, CO_2 \times {1 \, g \over 1000 \, mg } \times {1 \, mol \, CO_2 \over 44.010 \, g \, CO_2} \times {1 \, mol C \over 1 \, mol \, CO_2 } \times {12.011 \,g \over 1 \, mol \, C} \]

\[ = 1.883 \times 10^{-2} \, g \, C \]

\[ mass \, of \, H = 11.30 \, mg \, H_2O \times {1 \, g \over 1000 \, mg } \times {1 \, mol \, H_2O \over 18.015 \, g \, H_2O} \times {2 \, mol H \over 1 \, mol \, H_2O } \times {1.0079 \,g \over 1 \, mol \, H} \]

\[ = 1.264 \times 10^{-3} \, g \, H \]

B To obtain the relative numbers of atoms of both elements present, we need to calculate the number of moles of each and divide by the number of moles of the element present in the smallest amount:

\[ moles \, C = 1.883 \times 10^{-2} \,g \, C \times {1 \, mol \, C \over 12.011 \, g \, C} = 1.568 \times 10^{-3} \, mol C \]

\[ moles \, H = 1.264 \times 10^{-3} \,g \, H \times {1 \, mol \, H \over 1.0079 \, g \, H} = 1.254 \times 10^{-3} \, mol H \]

Dividing each number by the number of moles of the element present in the smaller amount gives

\[H: {1.254\times 10^{−3} \over 1.254 \times 10^{−3}} = 1.000 \, \, \, C: {1.568 \times 10^{−3} \over 1.254 \times 10^{−3}}= 1.250\]

Thus naphthalene contains a 1.25:1 ratio of moles of carbon to moles of hydrogen: C_1.25H_1.0. Because the ratios of the elements in the empirical formula must be expressed as small whole numbers, multiply both subscripts by 4, which gives C₅H₄ as the empirical formula of naphthalene. In fact, the molecular formula of naphthalene is C₁₀H₈, which is consistent with our results.

Exercise \(\PageIndex{1}\)

Xylene, an organic compound that is a major component of many gasoline blends, contains carbon and hydrogen only. Complete combustion of a 17.12 mg sample of xylene in oxygen yielded 56.77 mg of CO₂ and 14.53 mg of H₂O. Determine the empirical formula of xylene.
The empirical formula of benzene is CH (its molecular formula is C₆H₆). If 10.00 mg of benzene is subjected to combustion analysis, what mass of CO₂ and H₂O will be produced?

Answer a: The empirical formula is C₄H₅. (The molecular formula of xylene is actually C₈H₁₀.)
Answer b: 33.81 mg of CO₂; 6.92 mg of H₂O

Contributors and Attributions

Mike Blaber (Florida State University)
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).