5.5: Thermodynamics (Exercises)

16.1: Spontaneity Exercises

Q16.1.1

What is a spontaneous reaction?

S16.1.1

A reaction has a natural tendency to occur and takes place without the continual input of energy from an external source.

Q16.1.2

What is a nonspontaneous reaction?

Q16.1.3

Indicate whether the following processes are spontaneous or nonspontaneous.

1. Liquid water freezing at a temperature below its freezing point
2. Liquid water freezing at a temperature above its freezing point
3. The combustion of gasoline
4. A ball thrown into the air
5. A raindrop falling to the ground
6. Iron rusting in a moist atmosphere

S16.1.2

spontaneous; nonspontaneous; spontaneous; nonspontaneous; spontaneous; spontaneous

Q16.1.4

A helium-filled balloon spontaneously deflates overnight as He atoms diffuse through the wall of the balloon. Describe the redistribution of matter and/or energy that accompanies this process.

Q16.1.5

Many plastic materials are organic polymers that contain carbon and hydrogen. The oxidation of these plastics in air to form carbon dioxide and water is a spontaneous process; however, plastic materials tend to persist in the environment. Explain.

S16.1.5

Although the oxidation of plastics is spontaneous, the rate of oxidation is very slow. Plastics are therefore kinetically stable and do not decompose appreciably even over relatively long periods of time.

16.2: Entropy Exercises

Q16.2.1

In the below Figure all possible distributions and microstates are shown for four different particles shared between two boxes. Determine the entropy change, ΔS, if the particles are initially evenly distributed between the two boxes, but upon redistribution all end up in Box (b).

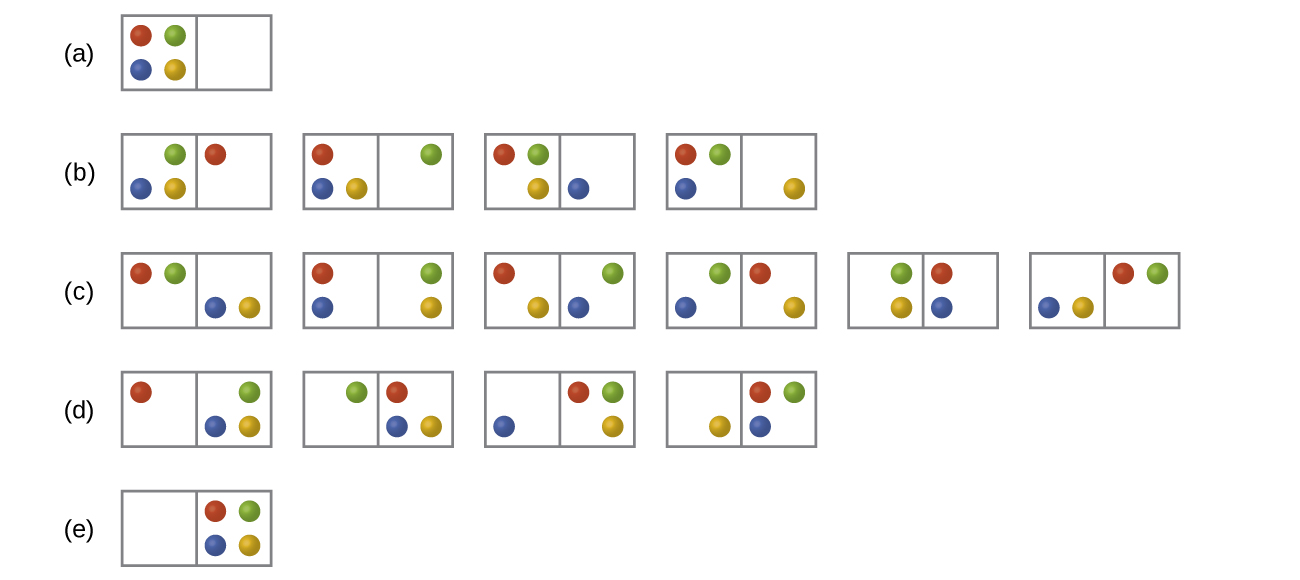
Q16.2.2

In Figure all of the possible distributions and microstates are shown for four different particles shared between two boxes. Determine the entropy change, ΔS, for the system when it is converted from distribution to distribution (d).

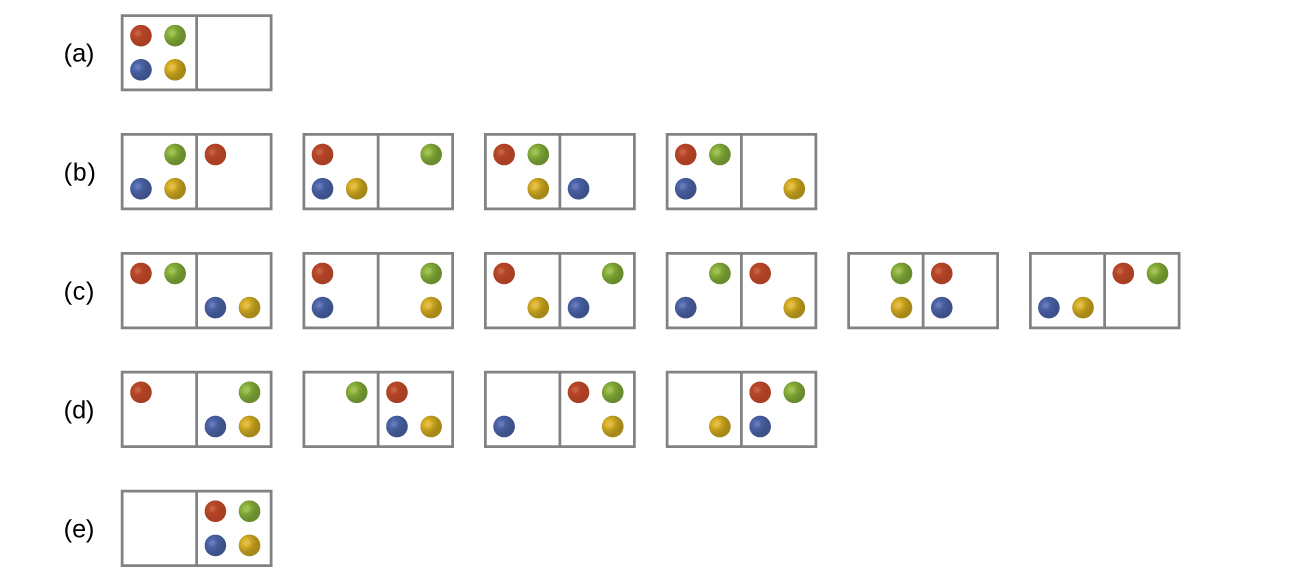
S16.2.2

There are four initial microstates and four final microstates.

\[ΔS=k\ln\dfrac{W_\ce{f}}{W_\ce{i}}=\mathrm{1.38×10^{−23}\:J/K×\ln\dfrac{4}{4}=0}\]

Q16.2.3

How does the process described in the previous item relate to the system shown in [link]?

Q16.2.4

Consider a system similar to the one below, except that it contains six particles instead of four. What is the probability of having all the particles in only one of the two boxes in the case? Compare this with the similar probability for the system of four particles that we have derived to be equal to \(\dfrac{1}{8}\). What does this comparison tell us about even larger systems?

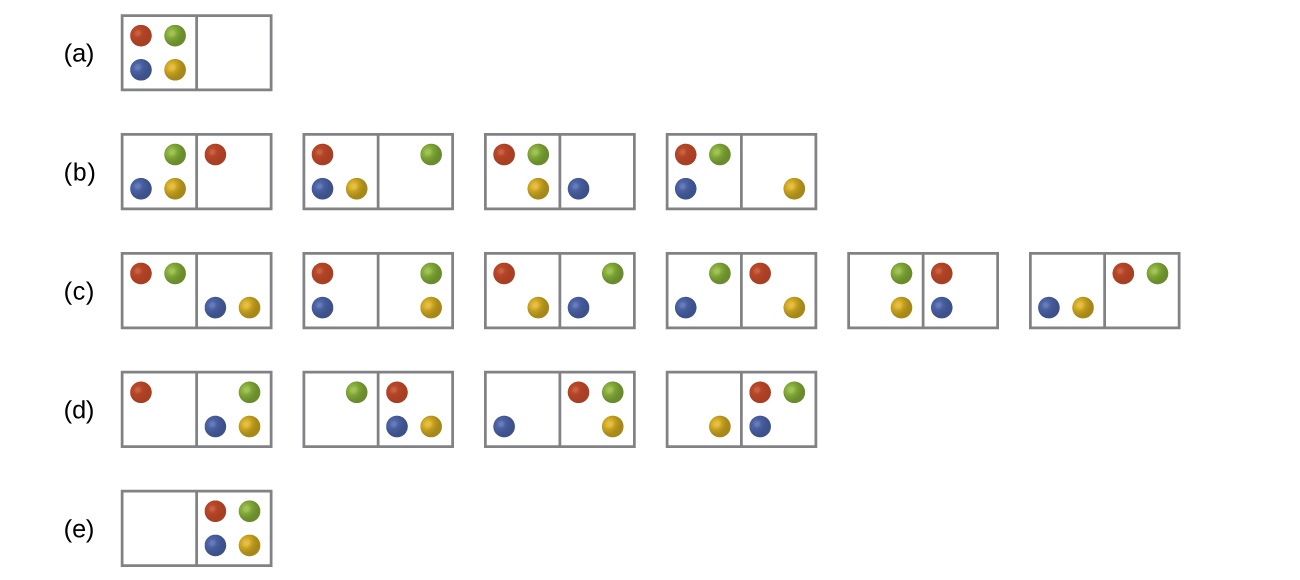
S16.2.4

The probability for all the particles to be on one side is \(\dfrac{1}{32}\). This probability is noticeably lower than the \(\dfrac{1}{8}\) result for the four-particle system. The conclusion we can make is that the probability for all the particles to stay in only one part of the system will decrease rapidly as the number of particles increases, and, for instance, the probability for all molecules of gas to gather in only one side of a room at room temperature and pressure is negligible since the number of gas molecules in the room is very large.

Q16.2.5

Consider the system shown in Figure. What is the change in entropy for the process where the energy is initially associated only with particle A, but in the final state the energy is distributed between two different particles?

Q16.2.6

Consider the system shown in Figure. What is the change in entropy for the process where the energy is initially associated with particles A and B, and the energy is distributed between two particles in different boxes (one in A-B, the other in C-D)?

S16.2.6

There is only one initial state. For the final state, the energy can be contained in pairs A-C, A-D, B-C, or B-D. Thus, there are four final possible states.

\[ΔS=k\ln\left(\dfrac{W_\ce{f}}{W_\ce{i}}\right)=\mathrm{1.38×10^{−23}\:J/K×\ln\left(\dfrac{4}{1}\right)=1.91×10^{−23}\:J/K}\]

Q16.2.7

Arrange the following sets of systems in order of increasing entropy. Assume one mole of each substance and the same temperature for each member of a set.

1. H₂(g), HBrO₄(g), HBr(g)
2. H₂O(l), H₂O(g), H₂O(s)
3. He(g), Cl₂(g), P₄(g)

Q16.2.8

At room temperature, the entropy of the halogens increases from I₂ to Br₂ to Cl₂. Explain.

S16.2.8

The masses of these molecules would suggest the opposite trend in their entropies. The observed trend is a result of the more significant variation of entropy with a physical state. At room temperature, I₂ is a solid, Br₂ is a liquid, and Cl₂ is a gas.

Q16.2.9

Consider two processes: sublimation of I₂(s) and melting of I₂(s) (Note: the latter process can occur at the same temperature but somewhat higher pressure).

\[\ce{I2}(s)⟶\ce{I2}(g)\]

\[\ce{I2}(s)⟶\ce{I2}(l)\]

Is ΔS positive or negative in these processes? In which of the processes will the magnitude of the entropy change be greater?

Q16.2.11

Indicate which substance in the given pairs has the higher entropy value. Explain your choices.

1. C₂H₅OH(l) or C₃H₇OH(l)
2. C₂H₅OH(l) or C₂H₅OH(g)
3. 2Hor H(g)

S16.2.11

C₃H₇OH(l) as it is a larger molecule (more complex and more massive), and so more microstates describing its motions are available at any given temperature. C₂H₅OH(g) as it is in the gaseous state. 2H(g), since entropy is an extensive property, and so two H atoms (or two moles of H atoms) possess twice as much entropy as one atom (or one mole of atoms).

Q16.2.11

Predict the sign of the entropy change for the following processes:

1. An ice cube is warmed to near its melting point.
2. Exhaled breath forms fog on a cold morning.
3. Snow melts.

Q16.2.12

Predict the sign of the enthalpy change for the following processes. Give a reason for your prediction.

1. \(\ce{Pb^2+}(aq)+\ce{S^2-}(aq)⟶\ce{PbS}(s)\)
2. \(\ce{2Fe}(s)+\ce{3O2}(g)⟶\ce{Fe2O3}(s)\)
3. \(\ce{2C6H14}(l)+\ce{19O2}(g)⟶\ce{14H2O}(g)+\ce{12CO2}(g)\)

S16.2.12

Negative. The relatively ordered solid precipitating decreases the number of mobile ions in solution. Negative. There is a net loss of three moles of gas from reactants to products. Positive. There is a net increase of seven moles of gas from reactants to products.

Q16.2.13

Write the balanced chemical equation for the combustion of methane, CH₄(g), to give carbon dioxide and water vapor. Explain why it is difficult to predict whether ΔS is positive or negative for this chemical reaction.

Q16.2.14

Write the balanced chemical equation for the combustion of benzene, C₆H₆(l), to give carbon dioxide and water vapor. Would you expect ΔS to be positive or negative in this process?

S16.2.14

\[\ce{C6H6}(l)+7.5\ce{O2}(g)⟶\ce{3H2O}(g)+\ce{6CO2}(g)\]

There are 7.5 moles of gas initially, and 3 + 6 = 9 moles of gas in the end. Therefore, it is likely that the entropy increases as a result of this reaction, and ΔS is positive.

16.3: The Second and Third law

Q16.3.0

What is the difference between ΔS, ΔS°, and \(ΔS^\circ_{298}\) for a chemical change?

Q16.3.1

Calculate \(ΔS^\circ_{298}\) for the following changes.

1. \(\ce{SnCl4}(l)⟶\ce{SnCl4}(g)\)
2. \(\ce{CS2}(g)⟶\ce{CS2}(l)\)
3. \(\ce{Cu}(s)⟶\ce{Cu}(g)\)
4. \(\ce{H2O}(l)⟶\ce{H2O}(g)\)
5. \(\ce{2H2}(g)+\ce{O2}(g)⟶\ce{2H2O}(l)\)
6. \(\ce{2HCl}(g)+\ce{Pb}(s)⟶\ce{PbCl2}(s)+\ce{H2}(g)\)
7. \(\ce{Zn}(s)+\ce{CuSO4}(s)⟶\ce{Cu}(s)+\ce{ZnSO4}(s)\)

S16.3.1

107 J/K; −86.4 J/K; 133.2 J/K; 118.8 J/K; −326.6 J/K; −171.9 J/K; (g) −7.2 J/K

Q16.3.2

Determine the entropy change for the combustion of liquid ethanol, C₂H₅OH, under standard state conditions to give gaseous carbon dioxide and liquid water.

Q16.3.3

Determine the entropy change for the combustion of gaseous propane, C₃H₈, under standard state conditions to give gaseous carbon dioxide and water.

S16.3.3

100.6 J/K

Q16.3.4

“Thermite” reactions have been used for welding metal parts such as railway rails and in metal refining. One such thermite reaction is:

\[\ce{Fe2O3}(s)+\ce{2Al}(s)⟶\ce{Al2O3}(s)+\ce{2Fe}(s)\]

Is the reaction spontaneous at room temperature under standard conditions? During the reaction, the surroundings absorb 851.8 kJ/mol of heat.

Q16.3.5

Using the relevant \(S^\circ_{298}\) values listed in Appendix G, calculate \(S^\circ_{298}\) for the following changes:

1. \(\ce{N2}(g)+\ce{3H2}(g)⟶\ce{2NH3}(g)\)
2. \(\ce{N2}(g)+\dfrac{5}{2}\ce{O2}(g)⟶\ce{N2O5}(g)\)

S16.3.5

−198.1 J/K; −348.9 J/K

Q16.3.6

From the following information, determine \(ΔS^\circ_{298}\) for the following:

1. \(\ce{N}(g)+\ce{O}(g)⟶\ce{NO}(g) \hspace{20px} ΔS^\circ_{298}=\,?\)
2. \(\ce{N2}(g)+\ce{O2}(g)⟶\ce{2NO}(g) \hspace{20px} ΔS^\circ_{298}=\mathrm{24.8\: J/K}\)
3. \(\ce{N2}(g)⟶\ce{2N}(g) \hspace{20px} ΔS^\circ_{298}=\mathrm{115.0\: J/K}\)
4. \(\ce{O2}(g)⟶\ce{2O}(g) \hspace{20px} ΔS^\circ_{298}=\mathrm{117.0\: J/K}\)

Q16.3.7

By calculating ΔS_univ at each temperature, determine if the melting of 1 mole of NaCl(s) is spontaneous at 500 °C and at 700 °C.

\[S^\circ_{\ce{NaCl}(s)}=\mathrm{72.11\:\dfrac{J}{mol⋅K}}\hspace{40px} S^\circ_{\ce{NaCl}(l)}=\mathrm{95.06\:\dfrac{J}{mol⋅K}}\hspace{40px ΔH^\circ_\ce{fusion}=\mathrm{27.95\: kJ/mol}\]

What assumptions are made about the thermodynamic information (entropy and enthalpy values) used to solve this problem?

S16.3.7

As ΔS_univ < 0 at each of these temperatures, melting is not spontaneous at either of them. The given values for entropy and enthalpy are for NaCl at 298 K. It is assumed that these do not change significantly at the higher temperatures used in the problem.

Q16.3.8

Use the standard entropy data in Appendix G to determine the change in entropy for each of the reactions listed in [link]. All are run under standard state conditions and 25 °C.

Q16.3.8

2.86 J/K; 24.8 J/K; −113.2 J/K; −24.7 J/K; 15.5 J/K; 290.0 J/K

16.4: Free Energy

Q16.4.1

What is the difference between ΔG, ΔG°, and \(ΔG^\circ_{298}\) for a chemical change?

Q16.4.2

A reactions has \(ΔH^\circ_{298}\) = 100 kJ/mol and \(ΔS^\circ_{298}=\textrm{250 J/mol⋅K}\). Is the reaction spontaneous at room temperature? If not, under what temperature conditions will it become spontaneous?

S16.4.2

The reaction is nonspontaneous at room temperature. Above 400 K, ΔG will become negative, and the reaction will become spontaneous.

Q16.4.3

Explain what happens as a reaction starts with ΔG < 0 (negative) and reaches the point where ΔG = 0.

Use the standard free energy of formation data in Appendix G to determine the free energy change for each of the following reactions, which are run under standard state conditions and 25 °C. Identify each as either spontaneous or nonspontaneous at these conditions.

1. \(\ce{MnO2}(s)⟶\ce{Mn}(s)+\ce{O2}(g)\)
2. \(\ce{H2}(g)+\ce{Br2}(l)⟶\ce{2HBr}(g)\)
3. \(\ce{Cu}(s)+\ce{S}(g)⟶\ce{CuS}(s)\)
4. \(\ce{2LiOH}(s)+\ce{CO2}(g)⟶\ce{Li2CO3}(s)+\ce{H2O}(g)\)
5. \(\ce{CH4}(g)+\ce{O2}(g)⟶\ce{C}(s,\,\ce{graphite})+\ce{2H2O}(g)\)
6. \(\ce{CS2}(g)+\ce{3Cl2}(g)⟶\ce{CCl4}(g)+\ce{S2Cl2}(g)\)

S16.4.3

465.1 kJ nonspontaneous; −106.86 kJ spontaneous; −53.6 kJ spontaneous; −83.4 kJ spontaneous; −406.7 kJ spontaneous; −30.0 kJ spontaneous

Q16.4.4

Use the standard free energy data in Appendix G to determine the free energy change for each of the following reactions, which are run under standard state conditions and 25 °C. Identify each as either spontaneous or nonspontaneous at these conditions.

1. \(\ce{C}(s,\, \ce{graphite})+\ce{O2}(g)⟶\ce{CO2}(g)\)
2. \(\ce{O2}(g)+\ce{N2}(g)⟶\ce{2NO}(g)\)
3. \(\ce{2Cu}(s)+\ce{S}(g)⟶\ce{Cu2S}(s)\)
4. \(\ce{CaO}(s)+\ce{H2O}(l)⟶\ce{Ca(OH)2}(s)\)
5. \(\ce{Fe2O3}(s)+\ce{3CO}(g)⟶\ce{2Fe}(s)+\ce{3CO2}(g)\)
6. \(\ce{CaSO4⋅2H2O}(s)⟶\ce{CaSO4}(s)+\ce{2H2O}(g)\)

Given:

\[\ce{P4}(s)+\ce{5O2}(g)⟶\ce{P4O10}(s) \hspace{20px} ΔG^\circ_{298}=\mathrm{−2697.0\: kJ/mol}\]

\[\ce{2H2}(g)+\ce{O2}(g)⟶\ce{2H2O}(g) \hspace{20px} ΔG^\circ_{298}=\mathrm{−457.18\: kJ/mol}\]

\[\ce{6H2O}(g)+\ce{P4O10}(g)⟶\ce{4H3PO4}(l) \hspace{20px} ΔG^\circ_{298}=\mathrm{−428.66\: kJ/mol}\]

Q16.4.5

1. Determine the standard free energy of formation, \(ΔG^\circ_\ce{f}\), for phosphoric acid.
2. How does your calculated result compare to the value in Appendix G? Explain.

S16.4.5

−1124.3 kJ/mol for the standard free energy change. The calculation agrees with the value in Appendix G because free energy is a state function (just like the enthalpy and entropy), so its change depends only on the initial and final states, not the path between them.

Q16.4.6

Is the formation of ozone (O₃(g)) from oxygen (O₂(g)) spontaneous at room temperature under standard state conditions?

Q16.4.7

Consider the decomposition of red mercury(II) oxide under standard state conditions.

\[\ce{2HgO}(s,\,\ce{red})⟶\ce{2Hg}(l)+\ce{O2}(g)\]

1. Is the decomposition spontaneous under standard state conditions?
2. Above what temperature does the reaction become spontaneous?

S16.4.7

The reaction is nonspontaneous; Above 566 °C the process is spontaneous.

Q16.4.8

Among other things, an ideal fuel for the control thrusters of a space vehicle should decompose in a spontaneous exothermic reaction when exposed to the appropriate catalyst. Evaluate the following substances under standard state conditions as suitable candidates for fuels.

1. Ammonia: \(\ce{2NH3}(g)⟶\ce{N2}(g)+\ce{3H2}(g)\)
2. Diborane: \(\ce{B2H6}(g)⟶\ce{2B}(g)+\ce{3H2}(g)\)
3. Hydrazine: \(\ce{N2H4}(g)⟶\ce{N2}(g)+\ce{2H2}(g)\)
4. Hydrogen peroxide: \(\ce{H2O2}(l)⟶\ce{H2O}(g)+\dfrac{1}{2}\ce{O2}(g)\)

Q16.4.9

Calculate ΔG° for each of the following reactions from the equilibrium constant at the temperature given.

1. \(\ce{N2}(g)+\ce{O2}(g)⟶\ce{2NO}(g) \hspace{20px} \mathrm{T=2000\:°C} \hspace{20px} K_p=4.1×10^{−4}\)
2. \(\ce{H2}(g)+\ce{I2}(g)⟶\ce{2HI}(g) \hspace{20px} \mathrm{T=400\:°C} \hspace{20px} K_p=50.0\)
3. \(\ce{CO2}(g)+\ce{H2}(g)⟶\ce{CO}(g)+\ce{H2O}(g) \hspace{20px} \mathrm{T=980\:°C} \hspace{20px} K_p=1.67\)
4. \(\ce{CaCO3}(s)⟶\ce{CaO}(s)+\ce{CO2}(g) \hspace{20px} \mathrm{T=900\:°C} \hspace{20px} K_p=1.04\)
5. \(\ce{HF}(aq)+\ce{H2O}(l)⟶\ce{H3O+}(aq)+\ce{F-}(aq) \hspace{20px} \mathrm{T=25\:°C} \hspace{20px} K_p=7.2×10^{−4}\)
6. \(\ce{AgBr}(s)⟶\ce{Ag+}(aq)+\ce{Br-}(aq) \hspace{20px} \mathrm{T=25\:°C} \hspace{20px} K_p=3.3×10^{−13}\)

S16.4.9

1.5 × 10² kJ; −21.9 kJ; −5.34 kJ; −0.383 kJ; 18 kJ; 71 kJ

Q16.4.10

Calculate ΔG° for each of the following reactions from the equilibrium constant at the temperature given.

1. \(\ce{Cl2}(g)+\ce{Br2}(g)⟶\ce{2BrCl}(g) \hspace{20px} \mathrm{T=25\:°C} \hspace{20px} K_p=4.7×10^{−2}\)
2. \(\ce{2SO2}(g)+\ce{O2}(g)⇌\ce{2SO3}(g) \hspace{20px} \mathrm{T=500\:°C} \hspace{20px} K_p=48.2\)
3. \(\ce{H2O}(l)⇌\ce{H2O}(g) \hspace{20px} \mathrm{T=60\:°C} \hspace{20px} K_p=\mathrm{0.196\: atm}\)
4. \(\ce{CoO}(s)+\ce{CO}(g)⇌\ce{Co}(s)+\ce{CO2}(g) \hspace{20px} \mathrm{T=550\:°C} \hspace{20px} K_p=4.90×10^2\)
5. \(\ce{CH3NH2}(aq)+\ce{H2O}(l)⟶\ce{CH3NH3+}(aq)+\ce{OH-}(aq) \hspace{20px} \mathrm{T=25\:°C} \hspace{20px} K_p=4.4×10^{−4}\)
6. \(\ce{PbI2}(s)⟶\ce{Pb^2+}(aq)+\ce{2I-}(aq) \hspace{20px} \mathrm{T=25\:°C} \hspace{20px} K_p=8.7×10^{−9}\)

Q16.4.11

Calculate the equilibrium constant at 25 °C for each of the following reactions from the value of ΔG° given.

1. \(\ce{O2}(g)+\ce{2F2}(g)⟶\ce{2OF2}(g) \hspace{20px} ΔG°=\mathrm{−9.2\: kJ}\)
2. \(\ce{I2}(s)+\ce{Br2}(l)⟶\ce{2IBr}(g) \hspace{20px} ΔG°=\mathrm{7.3\: kJ}\)
3. \(\ce{2LiOH}(s)+\ce{CO2}(g)⟶\ce{Li2CO3}(s)+\ce{H2O}(g) \hspace{20px} ΔG°=\mathrm{−79\: kJ}\)
4. \(\ce{N2O3}(g)⟶\ce{NO}(g)+\ce{NO2}(g) \hspace{20px} ΔG°=\mathrm{−1.6\: kJ}\)
5. \(\ce{SnCl4}(l)⟶\ce{SnCl4}(l) \hspace{20px} ΔG°=\mathrm{8.0\: kJ}\)

S16.4.11

K = 41; K = 0.053; K = 6.9 × 10¹³; K = 1.9; K = 0.04

Q16.4.2

Calculate the equilibrium constant at 25 °C for each of the following reactions from the value of ΔG° given.

1. \(\ce{I2}(s)+\ce{Cl2}(g)⟶\ce{2ICl}(g) \hspace{20px} ΔG°=\mathrm{−10.88\: kJ}\)
2. \(\ce{H2}(g)+\ce{I2}(s)⟶\ce{2HI}(g) \hspace{20px} ΔG°=\mathrm{3.4\: kJ}\)
3. \(\ce{CS2}(g)+\ce{3Cl2}(g)⟶\ce{CCl4}(g)+\ce{S2Cl2}(g) \hspace{20px} ΔG°=\mathrm{−39\: kJ}\)
4. \(\ce{2SO2}(g)+\ce{O2}(g)⟶\ce{2SO3}(g) \hspace{20px} ΔG°=\mathrm{−141.82\: kJ}\)
5. \(\ce{CS2}(g)⟶\ce{CS2}(l) \hspace{20px} ΔG°=\mathrm{−1.88\: kJ}\)

Q16.4.13

Calculate the equilibrium constant at the temperature given.

1. (a) \(\ce{O2}(g)+\ce{2F2}(g)⟶\ce{2F2O}(g) \hspace{20px} \mathrm{(T=100\:°C)}\)
2. \(\ce{I2}(s)+\ce{Br2}(l)⟶\ce{2IBr}(g) \hspace{20px} \mathrm{(T=0.0\:°C)}\)
3. \(\ce{2LiOH}(s)+\ce{CO2}(g)⟶\ce{Li2CO3}(s)+\ce{H2O}(g) \hspace{20px} \mathrm{(T=575\:°C)}\)
4. \(\ce{N2O3}(g)⟶\ce{NO}(g)+\ce{NO2}(g) \hspace{20px} \mathrm{(T=−10.0\:°C)}\)
5. \(\ce{SnCl4}(l)⟶\ce{SnCl4}(g) \hspace{20px} \mathrm{(T=200\:°C)}\)

S16.4.13

In each of the following, the value of ΔG is not given at the temperature of the reaction. Therefore, we must calculate ΔG° from the values ΔH° and ΔS° and then calculate ΔG from the relation ΔG° = ΔH° − TΔS°.

1. K = 1.29
2. K = 2.51 × 10⁻³
3. K = 4.83 × 10³
4. K = 0.219
5. K = 16.1

Q16.4.14

Calculate the equilibrium constant at the temperature given.

1. (a) \(\ce{I2}(s)+\ce{Cl2}(g)⟶\ce{2ICl}(g) \hspace{20px} \mathrm{(T=100\:°C)}\)
2. \(\ce{H2}(g)+\ce{I2}(s)⟶\ce{2HI}(g) \hspace{20px} \mathrm{(T=0.0\:°C)}\)
3. \(\ce{CS2}(g)+\ce{3Cl2}(g)⟶\ce{CCl4}(g)+\ce{S2Cl2}(g) \hspace{20px} \mathrm{(T=125\:°C)}\)
4. \(\ce{2SO2}(g)+\ce{O2}(g)⟶\ce{2SO3}(g) \hspace{20px} \mathrm{(T=675\:°C)}\)
5. \(\ce{CS2}(g)⟶\ce{CS2}(l) \hspace{20px} \mathrm{(T=90\:°C)}\)

Q16.4.15

Consider the following reaction at 298 K:

\[\ce{N2O4}(g)⇌\ce{2NO2}(g) \hspace{20px} K_P=0.142\]

What is the standard free energy change at this temperature? Describe what happens to the initial system, where the reactants and products are in standard states, as it approaches equilibrium.

S16.4.16

The standard free energy change is \(ΔG^\circ_{298}=−RT\ln K=\mathrm{4.84\: kJ/mol}\). When reactants and products are in their standard states (1 bar or 1 atm), Q = 1. As the reaction proceeds toward equilibrium, the reaction shifts left (the amount of products drops while the amount of reactants increases): Q < 1, and \(ΔG_{298}\) becomes less positive as it approaches zero. At equilibrium, Q = K, and ΔG = 0.

Q16.4.17

Determine the normal boiling point (in kelvin) of dichloroethane, CH₂Cl₂. Find the actual boiling point using the Internet or some other source, and calculate the percent error in the temperature. Explain the differences, if any, between the two values.

Q16.4.18

Under what conditions is \(\ce{N2O3}(g)⟶\ce{NO}(g)+\ce{NO2}(g)\) spontaneous?

S16.4.18

The reaction will be spontaneous at temperatures greater than 287 K.

Q16.4.19

At room temperature, the equilibrium constant (K_w) for the self-ionization of water is 1.00 × 10⁻¹⁴. Using this information, calculate the standard free energy change for the aqueous reaction of hydrogen ion with hydroxide ion to produce water. (Hint: The reaction is the reverse of the self-ionization reaction.)

Q16.4.20

Hydrogen sulfide is a pollutant found in natural gas. Following its removal, it is converted to sulfur by the reaction \(\ce{2H2S}(g)+\ce{SO2}(g)⇌\dfrac{3}{8}\ce{S8}(s,\,\ce{rhombic})+\ce{2H2O}(l)\). What is the equilibrium constant for this reaction? Is the reaction endothermic or exothermic?

S16.4.20

K = 5.35 × 10¹⁵

The process is exothermic.

Q16.4.21

Consider the decomposition of CaCO₃(s) into CaO(s) and CO₂(g). What is the equilibrium partial pressure of CO₂ at room temperature?

Q16.4.22

In the laboratory, hydrogen chloride (HCl(g)) and ammonia (NH₃(g)) often escape from bottles of their solutions and react to form the ammonium chloride (NH₄Cl(s)), the white glaze often seen on glassware. Assuming that the number of moles of each gas that escapes into the room is the same, what is the maximum partial pressure of HCl and NH₃ in the laboratory at room temperature? (Hint: The partial pressures will be equal and are at their maximum value when at equilibrium.)

S16.4.22

1.0 × 10⁻⁸ atm. This is the maximum pressure of the gases under the stated conditions.

Q16.4.23

Benzene can be prepared from acetylene. \(\ce{3C2H2}(g)⇌\ce{C6H6}(g)\). Determine the equilibrium constant at 25 °C and at 850 °C. Is the reaction spontaneous at either of these temperatures? Why is all acetylene not found as benzene?

Q16.4.24

Carbon dioxide decomposes into CO and O₂ at elevated temperatures. What is the equilibrium partial pressure of oxygen in a sample at 1000 °C for which the initial pressure of CO₂ was 1.15 atm?

\[x=\mathrm{1.29×10^{−5}\:atm}=P_{\ce{O2}}\]

Q16.4.25

Carbon tetrachloride, an important industrial solvent, is prepared by the chlorination of methane at 850 K.

\[\ce{CH4}(g)+\ce{4Cl2}(g)⟶\ce{CCl4}(g)+\ce{4HCl}(g)\]

What is the equilibrium constant for the reaction at 850 K? Would the reaction vessel need to be heated or cooled to keep the temperature of the reaction constant?

Q16.4.25B

Acetic acid, CH₃CO₂H, can form a dimer, (CH₃CO₂H)₂, in the gas phase.

\[\ce{2CH3CO2H}(g)⟶\ce{(CH3CO2H)2}(g)\]

The dimer is held together by two hydrogen bonds with a total strength of 66.5 kJ per mole of dimer.

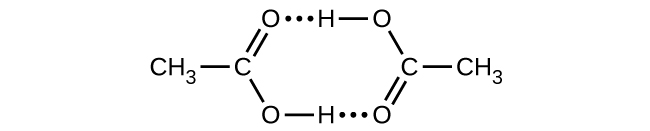
At 25 °C, the equilibrium constant for the dimerization is 1.3 × 10³ (pressure in atm). What is ΔS° for the reaction?

S16.4.25B

−0.16 kJ

Q16.4.26

Nitric acid, HNO₃, can be prepared by the following sequence of reactions:

\[\ce{4NH3}(g)+\ce{5O2}(g)⟶\ce{4NO}(g)+\ce{6H2O}(g)\]

\[\ce{2NO}(g)+\ce{O2}(g)⟶\ce{2NO2}(g)\]

\[\ce{3NO2}(g)+\ce{H2O}(l)⟶\ce{2HNO3}(l)+\ce{NO}(g)\]

How much heat is evolved when 1 mol of NH₃(g) is converted to HNO₃(l)? Assume standard states at 25 °C.

Q16.4.27A

Determine ΔG for the following reactions.

(a) Antimony pentachloride decomposes at 448 °C. The reaction is:

\[\ce{SbCl5}(g)⟶\ce{SbCl3}(g)+\ce{Cl2}(g)\]

An equilibrium mixture in a 5.00 L flask at 448 °C contains 3.85 g of SbCl₅, 9.14 g of SbCl₃, and 2.84 g of Cl₂.

Chlorine molecules dissociate according to this reaction:

\[\ce{Cl2}(g)⟶\ce{2Cl}(g)\]

1.00% of Cl₂ molecules dissociate at 975 K and a pressure of 1.00 atm.

S16.4.27A

1. (a) −22.1 kJ;
2. 61.6 kJ/mol

Q16.4.27

Given that the \(ΔG^\circ_\ce{f}\) for Pb²⁺(aq) and Cl⁻(aq) is −24.3 kJ/mole and −131.2 kJ/mole respectively, determine the solubility product, K_sp, for PbCl₂(s).

Q16.4.28

Determine the standard free energy change, \(ΔG^\circ_\ce{f}\), for the formation of S²⁻(aq) given that the \(ΔG^\circ_\ce{f}\) for Ag⁺(aq) and Ag₂S(s) are 77.1 k/mole and −39.5 kJ/mole respectively, and the solubility product for Ag₂S(s) is 8 × 10⁻⁵¹.

S16.4.28

90 kJ/mol

Q16.4.29

Determine the standard enthalpy change, entropy change, and free energy change for the conversion of diamond to graphite. Discuss the spontaneity of the conversion with respect to the enthalpy and entropy changes. Explain why diamond spontaneously changing into graphite is not observed.

Q16.4.30

The evaporation of one mole of water at 298 K has a standard free energy change of 8.58 kJ.

\[\ce{H2O}(l)⇌\ce{H2O}(g) \hspace{20px} ΔG^\circ_{298}=\mathrm{8.58\: kJ}\]

1. (a) Is the evaporation of water under standard thermodynamic conditions spontaneous?
2. Determine the equilibrium constant, K_P, for this physical process.
3. By calculating ∆G, determine if the evaporation of water at 298 K is spontaneous when the partial pressure of water, \(P_{\ce{H2O}}\), is 0.011 atm.
4. If the evaporation of water were always nonspontaneous at room temperature, wet laundry would never dry when placed outside. In order for laundry to dry, what must be the value of \(P_{\ce{H2O}}\) in the air?

S16.4.30

(a) Under standard thermodynamic conditions, the evaporation is nonspontaneous; K_p = 0.031; The evaporation of water is spontaneous; \(P_{\ce{H2O}}\) must always be less than K_p or less than 0.031 atm. 0.031 atm represents air saturated with water vapor at 25 °C, or 100% humidity.

Q16.4.31

In glycolysis, the reaction of glucose (Glu) to form glucose-6-phosphate (G6P) requires ATP to be present as described by the following equation:

\[\mathrm{Glu + ATP ⟶ G6P + ADP} \hspace{20px} ΔG^\circ_{298}=\mathrm{−17\: kJ}\]

In this process, ATP becomes ADP summarized by the following equation:

\[\mathrm{ATP⟶ADP} \hspace{20px} ΔG^\circ_{298}=\mathrm{−30\: kJ}\]

Determine the standard free energy change for the following reaction, and explain why ATP is necessary to drive this process:

\[\mathrm{Glu⟶G6P} \hspace{20px} ΔG^\circ_{298}=\:?\]

Q16.4.32

One of the important reactions in the biochemical pathway glycolysis is the reaction of glucose-6-phosphate (G6P) to form fructose-6-phosphate (F6P):

\[\mathrm{G6P⇌F6P} \hspace{20px} ΔG^\circ_{298}=\mathrm{1.7\: kJ}\]

1. (a) Is the reaction spontaneous or nonspontaneous under standard thermodynamic conditions?
2. Standard thermodynamic conditions imply the concentrations of G6P and F6P to be 1 M, however, in a typical cell, they are not even close to these values. Calculate ΔG when the concentrations of G6P and F6P are 120 μM and 28 μM respectively, and discuss the spontaneity of the forward reaction under these conditions. Assume the temperature is 37 °C.

S16.4.32

(a) Nonspontaneous as \(ΔG^\circ_{298}>0\); \(ΔG^\circ_{298}=−RT\ln K,\) \(ΔG = 1.7×10^3 + \left(8.314 × 335 × \ln\dfrac{28}{128}\right) = \mathrm{−2.5\: kJ}\). The forward reaction to produce F6P is spontaneous under these conditions.

Q16.4.33

Without doing a numerical calculation, determine which of the following will reduce the free energy change for the reaction, that is, make it less positive or more negative, when the temperature is increased. Explain.

1. (a) \(\ce{N2}(g)+\ce{3H2}(g)⟶\ce{2NH3}(g)\)
2. \(\ce{HCl}(g)+\ce{NH3}(g)⟶\ce{NH4Cl}(s)\)
3. \(\ce{(NH4)2Cr2O7}(s)⟶\ce{Cr2O3}(s)+\ce{4H2O}(g)+\ce{N2}(g)\)
4. \(\ce{2Fe}(s)+\ce{3O2}(g)⟶\ce{Fe2O3}(s)\)

When ammonium chloride is added to water and stirred, it dissolves spontaneously and the resulting solution feels cold. Without doing any calculations, deduce the signs of ΔG, ΔH, and ΔS for this process, and justify your choices.

S16.4.33

ΔG is negative as the process is spontaneous. ΔH is positive as with the solution becoming cold, the dissolving must be endothermic. ΔS must be positive as this drives the process, and it is expected for the dissolution of any soluble ionic compound.

Q16.4.34

An important source of copper is from the copper ore, chalcocite, a form of copper(I) sulfide. When heated, the Cu₂S decomposes to form copper and sulfur described by the following equation:

\[\ce{Cu2S}(s)⟶\ce{Cu}(s)+\ce{S}(s)\]

1. (a) Determine \(ΔG^\circ_{298}\) for the decomposition of Cu₂S(s).
2. The reaction of sulfur with oxygen yields sulfur dioxide as the only product. Write an equation that describes this reaction, and determine \(ΔG^\circ_{298}\) for the process.
3. The production of copper from chalcocite is performed by roasting the Cu₂S in air to produce the Cu. By combining the equations from Parts (a) and (b), write the equation that describes the roasting of the chalcocite, and explain why coupling these reactions together makes for a more efficient process for the production of the copper.

Q16.4.35

What happens to \(ΔG^\circ_{298}\) (becomes more negative or more positive) for the following chemical reactions when the partial pressure of oxygen is increased?

1. (a) \(\ce{S}(s)+\ce{O2}(g)⟶\ce{SO2}(g)\)
2. \(\ce{2SO2}(g)+\ce{O2}(g)⟶\ce{SO3}(g)\)
3. \(\ce{HgO}(s)⟶\ce{Hg}(l)+\ce{O2}(g)\)

S16.4.35

1. (a) Increasing \(P_{\ce{O2}}\) will shift the equilibrium toward the products, which increases the value of K. \(ΔG^\circ_{298}\) therefore becomes more negative.
2. Increasing \(P_{\ce{O2}}\) will shift the equilibrium toward the products, which increases the value of K. \(ΔG^\circ_{298}\) therefore becomes more negative.
3. Increasing \(P_{\ce{O2}}\) will shift the equilibrium the reactants, which decreases the value of K. \(ΔG^\circ_{298}\) therefore becomes more positive.