3.4.1: Molecular Shape
- Page ID
- 210711
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Predict the structures of small molecules using valence shell electron pair repulsion (VSEPR) theory
Thus far, we have used two-dimensional Lewis structures to represent molecules. However, molecular structure is actually three-dimensional, and it is important to be able to describe molecular bonds in terms of their distances, angles, and relative arrangements in space (Figure \(\PageIndex{1}\)). A bond angle is the angle between any two bonds that include a common atom, usually measured in degrees. A bond distance (or bond length) is the distance between the nuclei of two bonded atoms along the straight line joining the nuclei. Bond distances are measured in Ångstroms (1 Å = 10–10 m) or picometers (1 pm = 10–12 m, 100 pm = 1 Å).
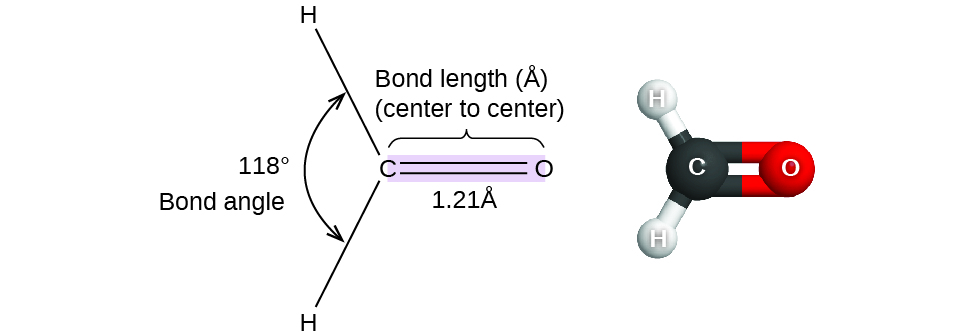
Figure \(\PageIndex{1}\): Bond distances (lengths) and angles are shown for the formaldehyde molecule, H2CO.
VSEPR Theory
Valence shell electron-pair repulsion theory (VSEPR theory) enables us to predict the molecular structure, including approximate bond angles around a central atom, of a molecule from an examination of the number of bonds and lone electron pairs in its Lewis structure. The VSEPR model assumes that electron pairs in the valence shell of a central atom will adopt an arrangement that minimizes repulsions between these electron pairs by maximizing the distance between them. The electrons in the valence shell of a central atom form either bonding pairs of electrons, located primarily between bonded atoms, or lone pairs. The electrostatic repulsion of these electrons is reduced when the various regions of high electron density assume positions as far from each other as possible.
VSEPR theory predicts the arrangement of electron pairs around each central atom and, usually, the correct arrangement of atoms in a molecule. We should understand, however, that the theory only considers electron-pair repulsions. Other interactions, such as nuclear-nuclear repulsions and nuclear-electron attractions, are also involved in the final arrangement that atoms adopt in a particular molecular structure.
As a simple example of VSEPR theory, let us predict the structure of a gaseous BeF2 molecule. The Lewis structure of BeF2 (Figure \(\PageIndex{2}\)) shows only two electron pairs around the central beryllium atom. With two bonds and no lone pairs of electrons on the central atom, the bonds are as far apart as possible, and the electrostatic repulsion between these regions of high electron density is reduced to a minimum when they are on opposite sides of the central atom. The bond angle is 180° (Figure \(\PageIndex{2}\)).
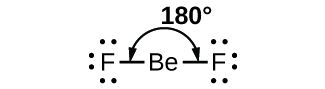
Figure \(\PageIndex{2}\): The BeF2 molecule adopts a linear structure in which the two bonds are as far apart as possible, on opposite sides of the Be atom.
Figure \(\PageIndex{3}\) illustrates this and other electron-pair geometries that minimize the repulsions among regions of high electron density (bonds and/or lone pairs). Two regions of electron density around a central atom in a molecule form a linear geometry; three regions form a trigonal planar geometry; four regions form a tetrahedral geometry; five regions form a trigonal bipyramidal geometry; and six regions form an octahedral geometry.
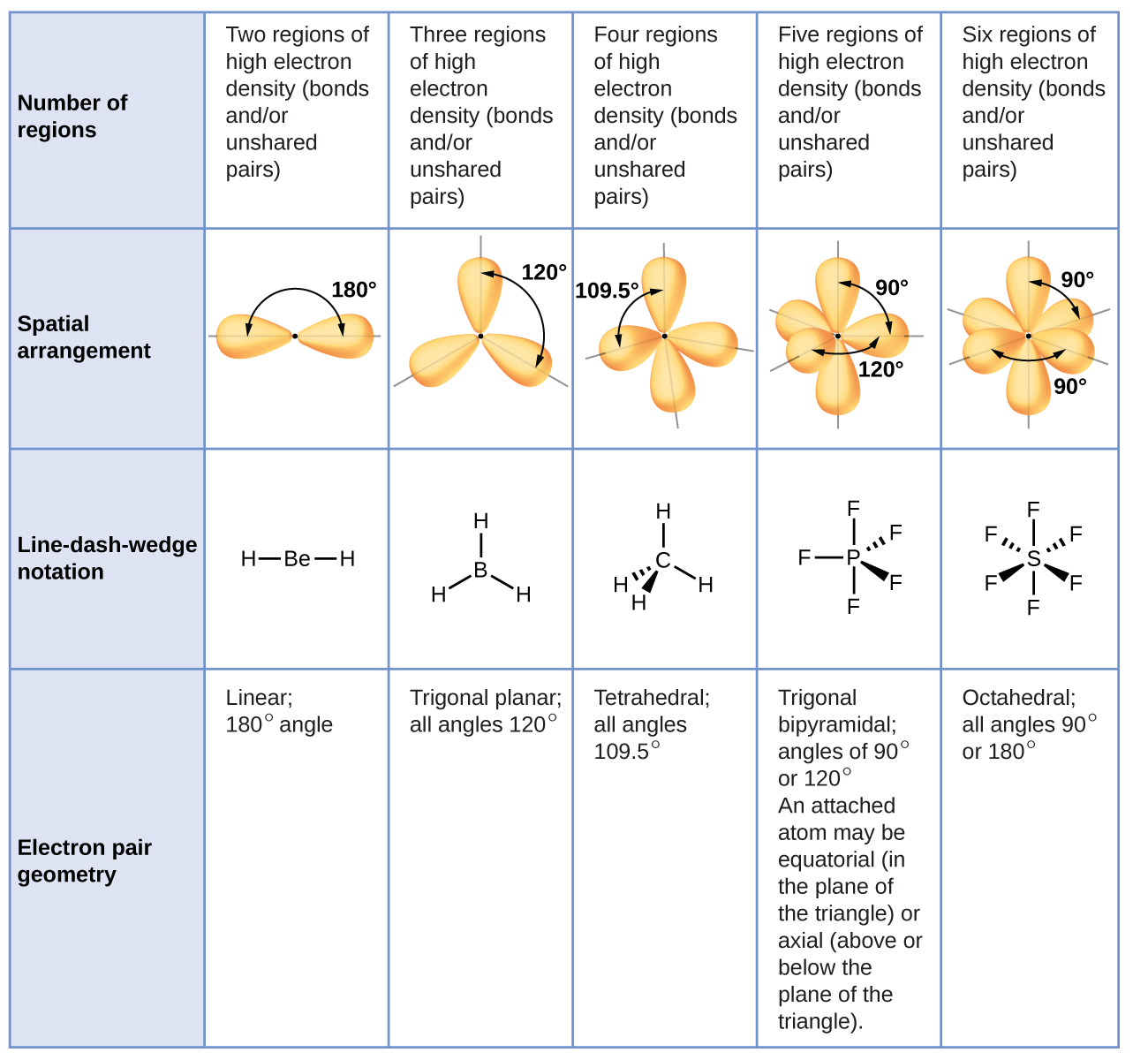
Figure \(\PageIndex{3}\): The basic electron-pair geometries predicted by VSEPR theory maximize the space around any region of electron density (bonds or lone pairs).
Electron-pair Geometry versus Molecular Structure
It is important to note that electron-pair geometry around a central atom is not the same thing as its molecular structure. The electron-pair geometries shown in Figure \(\PageIndex{3}\) describe all regions where electrons are located, bonds as well as lone pairs. Molecular structure describes the location of the atoms, not the electrons.
We differentiate between these two situations by naming the geometry that includes all electron pairs the electron-pair geometry. The structure that includes only the placement of the atoms in the molecule is called the molecular structure. The electron-pair geometries will be the same as the molecular structures when there are no lone electron pairs around the central atom, but they will be different when there are lone pairs present on the central atom.
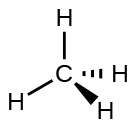
Figure \(\PageIndex{4}\): The molecular structure of the methane molecule, CH4, is shown with a tetrahedral arrangement of the hydrogen atoms. VSEPR structures like this one are often drawn using the wedge and dash notation, in which solid lines represent bonds in the plane of the page, solid wedges represent bonds coming up out of the plane, and dashed lines represent bonds going down into the plane.
For example, the methane molecule, CH4, which is the major component of natural gas, has four bonding pairs of electrons around the central carbon atom; the electron-pair geometry is tetrahedral, as is the molecular structure (Figure \(\PageIndex{4}\)). On the other hand, the ammonia molecule, NH3, also has four electron pairs associated with the nitrogen atom, and thus has a tetrahedral electron-pair geometry. One of these regions, however, is a lone pair, which is not included in the molecular structure, and this lone pair influences the shape of the molecule (Figure \(\PageIndex{5}\)).
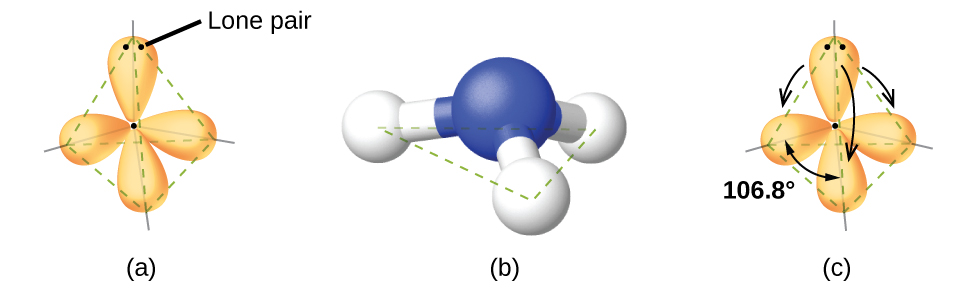
Figure \(\PageIndex{5}\): (a) The electron-pair geometry for the ammonia molecule is tetrahedral with one lone pair and three single bonds. (b) The trigonal pyramidal molecular structure is determined from the electron-pair geometry. (c) The actual bond angles deviate slightly from the idealized angles because the lone pair takes up a larger region of space than do the single bonds, causing the HNH angle to be slightly smaller than 109.5°.
Small distortions from the ideal angles in Figure \(\PageIndex{5}\) can result from differences in repulsion between various regions of electron density. VSEPR theory predicts these distortions by establishing an order of repulsions and an order of the amount of space occupied by different kinds of electron pairs. The order of electron-pair repulsions from greatest to least repulsion is:
lone pair-lone pair > lone pair-bonding pair > bonding pair-bonding pair
This order of repulsions determines the amount of space occupied by different regions of electrons. A lone pair of electrons occupies a larger region of space than the electrons in a triple bond; in turn, electrons in a triple bond occupy more space than those in a double bond, and so on. The order of sizes from largest to smallest is:
lone pair > triple bond > double bond > single bond
Consider formaldehyde, H2CO, which is used as a preservative for biological and anatomical specimens. This molecule has regions of high electron density that consist of two single bonds and one double bond. The basic geometry is trigonal planar with 120° bond angles, but we see that the double bond causes slightly larger angles (121°), and the angle between the single bonds is slightly smaller (118°).
In the ammonia molecule, the three hydrogen atoms attached to the central nitrogen are not arranged in a flat, trigonal planar molecular structure, but rather in a three-dimensional trigonal pyramid (Figure \(\PageIndex{6}\)) with the nitrogen atom at the apex and the three hydrogen atoms forming the base. The ideal bond angles in a trigonal pyramid are based on the tetrahedral electron pair geometry. Again, there are slight deviations from the ideal because lone pairs occupy larger regions of space than do bonding electrons. The H–N–H bond angles in NH3 are slightly smaller than the 109.5° angle in a regular tetrahedron (Figure \(\PageIndex{6}\)) because the lone pair-bonding pair repulsion is greater than the bonding pair-bonding pair repulsion. The ideal molecular structures are predicted based on the electron-pair geometries for various combinations of lone pairs and bonding pairs.
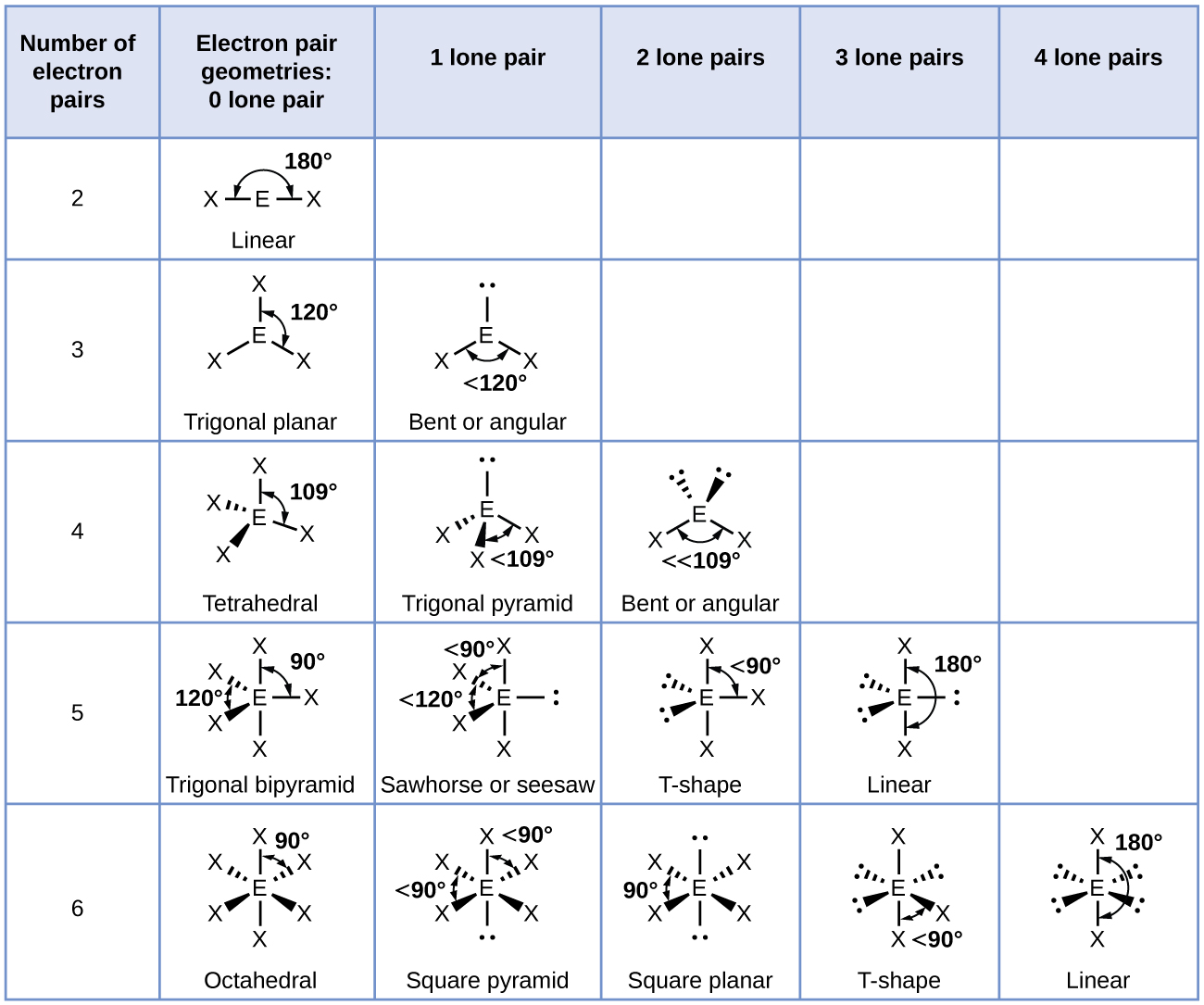
Figure \(\PageIndex{6}\): The molecular structures are identical to the electron-pair geometries when there are no lone pairs present (first column). For a particular number of electron pairs (row), the molecular structures for one or more lone pairs are determined based on modifications of the corresponding electron-pair geometry.
According to VSEPR theory, the terminal atom locations (Xs in Figure \(\PageIndex{7}\)) are equivalent within the linear, trigonal planar, and tetrahedral electron-pair geometries (the first three rows of the table). It does not matter which X is replaced with a lone pair because the molecules can be rotated to convert positions. For trigonal bipyramidal electron-pair geometries, however, there are two distinct X positions (Figure \(\PageIndex{7}\)a): an axial position (if we hold a model of a trigonal bipyramid by the two axial positions, we have an axis around which we can rotate the model) and an equatorial position (three positions form an equator around the middle of the molecule). The axial position is surrounded by bond angles of 90°, whereas the equatorial position has more space available because of the 120° bond angles. In a trigonal bipyramidal electron-pair geometry, lone pairs always occupy equatorial positions because these more spacious positions can more easily accommodate the larger lone pairs.
Theoretically, we can come up with three possible arrangements for the three bonds and two lone pairs for the ClF3 molecule (Figure \(\PageIndex{7}\)). The stable structure is the one that puts the lone pairs in equatorial locations, giving a T-shaped molecular structure.
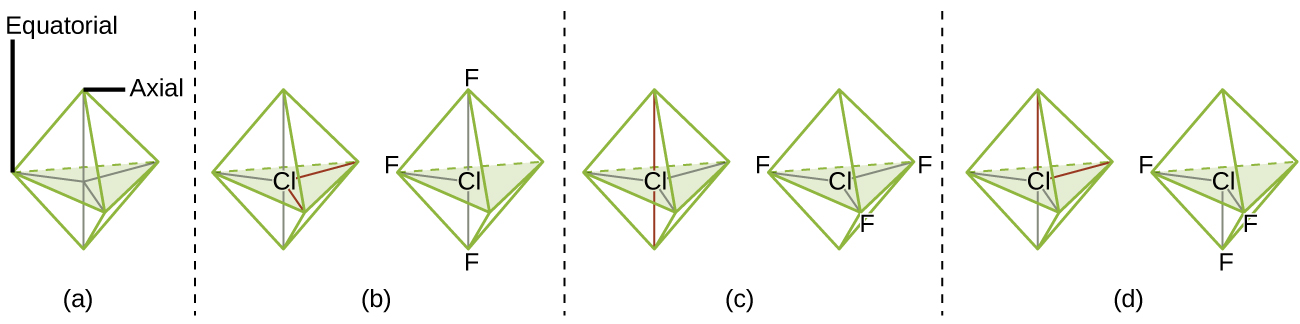
Figure \(\PageIndex{7}\): (a) In a trigonal bipyramid, the two axial positions are located directly across from one another, whereas the three equatorial positions are located in a triangular arrangement. (b–d) The two lone pairs (red lines) in ClF3 have several possible arrangements, but the T-shaped molecular structure (b) is the one actually observed, consistent with the larger lone pairs both occupying equatorial positions.
When a central atom has two lone electron pairs and four bonding regions, we have an octahedral electron-pair geometry. The two lone pairs are on opposite sides of the octahedron (180° apart), giving a square planar molecular structure that minimizes lone pair-lone pair repulsions.
Predicting Electron Pair Geometry and Molecular Structure
The following procedure uses VSEPR theory to determine the electron pair geometries and the molecular structures:
- Write the Lewis structure of the molecule or polyatomic ion.
- Count the number of regions of electron density (lone pairs and bonds) around the central atom. A single, double, or triple bond counts as one region of electron density.
- Identify the electron-pair geometry based on the number of regions of electron density: linear, trigonal planar, tetrahedral, trigonal bipyramidal, or octahedral (Figure \(\PageIndex{7}\), first column).
- Use the number of lone pairs to determine the molecular structure (Figure \(\PageIndex{7}\) ). If more than one arrangement of lone pairs and chemical bonds is possible, choose the one that will minimize repulsions, remembering that lone pairs occupy more space than multiple bonds, which occupy more space than single bonds. In trigonal bipyramidal arrangements, repulsion is minimized when every lone pair is in an equatorial position. In an octahedral arrangement with two lone pairs, repulsion is minimized when the lone pairs are on opposite sides of the central atom.
The following examples illustrate the use of VSEPR theory to predict the molecular structure of molecules or ions that have no lone pairs of electrons. In this case, the molecular structure is identical to the electron pair geometry.
Example \(\PageIndex{1}\): Predicting Electron-pair Geometry and Molecular Structure
Predict the electron-pair geometry and molecular structure for each of the following:
- carbon dioxide, CO2, a molecule produced by the combustion of fossil fuels
- boron trichloride, BCl3, an important industrial chemical
Solution
(a) We write the Lewis structure of CO2 as:

This shows us two regions of high electron density around the carbon atom—each double bond counts as one region, and there are no lone pairs on the carbon atom. Using VSEPR theory, we predict that the two regions of electron density arrange themselves on opposite sides of the central atom with a bond angle of 180°. The electron-pair geometry and molecular structure are identical, and CO2 molecules are linear.
(b) We write the Lewis structure of BCl3 as:
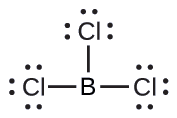
Thus we see that BCl3 contains three bonds, and there are no lone pairs of electrons on boron. The arrangement of three regions of high electron density gives a trigonal planar electron-pair geometry. The B–Cl bonds lie in a plane with 120° angles between them. BCl3 also has a trigonal planar molecular structure.
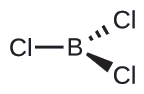
The electron-pair geometry and molecular structure of BCl3 are both trigonal planar. Note that the VSEPR geometry indicates the correct bond angles (120°), unlike the Lewis structure shown above.
Exercise \(\PageIndex{1}\)
Carbonate, \(\ce{CO3^2-}\), is a common polyatomic ion found in various materials from eggshells to antacids. What are the electron-pair geometry and molecular structure of this polyatomic ion?
- Answer
-
The electron-pair geometry is trigonal planar and the molecular structure is trigonal planar. Due to resonance, all three C–O bonds are identical. Whether they are single, double, or an average of the two, each bond counts as one region of electron density.
Example \(\PageIndex{2}\): Predicting Electron-pair Geometry and Molecular Structure
Two of the top 50 chemicals produced in the United States, ammonium nitrate and ammonium sulfate, both used as fertilizers, contain the ammonium ion. Predict the electron-pair geometry and molecular structure of the \(\ce{NH4+}\) cation.
Solution
We write the Lewis structure of \(\ce{NH4+}\) as:
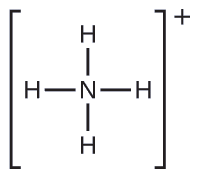
We can see that \(\ce{NH4+}\) contains four bonds from the nitrogen atom to hydrogen atoms and no lone pairs. We expect the four regions of high electron density to arrange themselves so that they point to the corners of a tetrahedron with the central nitrogen atom in the middle (Figure \(\PageIndex{7}\)). Therefore, the electron pair geometry of \(\ce{NH4+}\) is tetrahedral, and the molecular structure is also tetrahedral (Figure \(\PageIndex{7}\)).
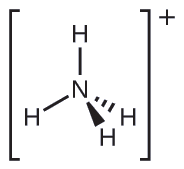
Figure \(\PageIndex{8}\): The ammonium ion displays a tetrahedral electron-pair geometry as well as a tetrahedral molecular structure.
Exercise \(\PageIndex{2}\)
Identify a molecule with trigonal bipyramidal molecular structure.
- Answer
-
Any molecule with five electron pairs around the central atoms including no lone pairs will be trigonal bipyramidal. \(\ce{PF5}\) is a common example
The next several examples illustrate the effect of lone pairs of electrons on molecular structure.
Example \(\PageIndex{3}\): Lone Pairs on the Central Atom
Predict the electron-pair geometry and molecular structure of a water molecule.
Solution
The Lewis structure of H2O indicates that there are four regions of high electron density around the oxygen atom: two lone pairs and two chemical bonds:
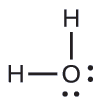
We predict that these four regions are arranged in a tetrahedral fashion (Figure \(\PageIndex{6}\)), as indicated in Figure \(\PageIndex{9}\). Thus, the electron-pair geometry is tetrahedral and the molecular structure is bent with an angle slightly less than 109.5°. In fact, the bond angle is 104.5°.
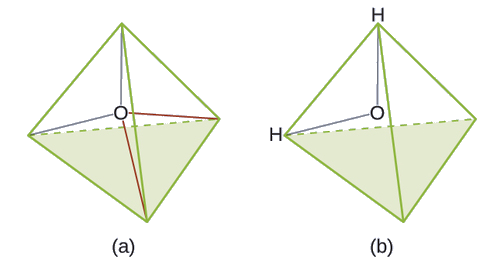
Figure \(\PageIndex{9}\): (a) H2O has four regions of electron density around the central atom, so it has a tetrahedral electron-pair geometry. (b) Two of the electron regions are lone pairs, so the molecular structure is bent.
Exercise \(\PageIndex{3}\)
The hydronium ion, H3O+, forms when acids are dissolved in water. Predict the electron-pair geometry and molecular structure of this cation.
- Answer
-
electron pair geometry: tetrahedral; molecular structure: trigonal pyramidal
Example \(\PageIndex{4}\): SF4 Sulfur tetrafluoride,
Predicting Electron-pair Geometry and Molecular Structure: SF4, is extremely valuable for the preparation of fluorine-containing compounds used as herbicides (i.e., SF4 is used as a fluorinating agent). Predict the electron-pair geometry and molecular structure of a SF4 molecule.
Solution
The Lewis structure of SF4 indicates five regions of electron density around the sulfur atom: one lone pair and four bonding pairs:
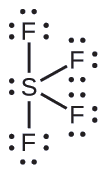
We expect these five regions to adopt a trigonal bipyramidal electron-pair geometry. To minimize lone pair repulsions, the lone pair occupies one of the equatorial positions. The molecular structure (Figure \(\PageIndex{6}\)) is that of a seesaw (Figure \(\PageIndex{10}\)).

Figure \(\PageIndex{10}\): (a) SF4 has a trigonal bipyramidal arrangement of the five regions of electron density. (b) One of the regions is a lone pair, which results in a seesaw-shaped molecular structure.
Exercise \(\PageIndex{4}\)
Predict the electron pair geometry and molecular structure for molecules of XeF2.
- Answer
-
The electron-pair geometry is trigonal bipyramidal. The molecular structure is linear.
Example \(\PageIndex{4}\): XeF4
Of all the noble gases, xenon is the most reactive, frequently reacting with elements such as oxygen and fluorine. Predict the electron-pair geometry and molecular structure of the XeF4 molecule.
Solution
The Lewis structure of XeF4 indicates six regions of high electron density around the xenon atom: two lone pairs and four bonds:
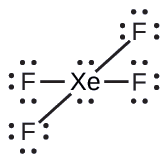
These six regions adopt an octahedral arrangement (Figure \(\PageIndex{6}\)), which is the electron-pair geometry. To minimize repulsions, the lone pairs should be on opposite sides of the central atom (Figure \(\PageIndex{11}\)). The five atoms are all in the same plane and have a square planar molecular structure.
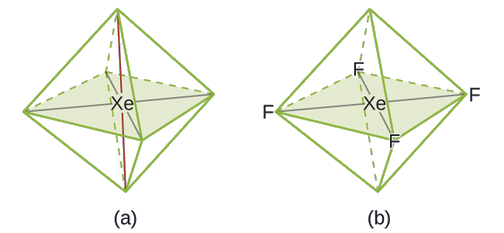
Figure \(\PageIndex{11}\): (a) XeF4 adopts an octahedral arrangement with two lone pairs (red lines) and four bonds in the electron-pair geometry. (b) The molecular structure is square planar with the lone pairs directly across from one another.
Exercise \(\PageIndex{4}\)
In a certain molecule, the central atom has three lone pairs and two bonds. What will the electron pair geometry and molecular structure be?
- Answer
-
electron pair geometry: trigonal bipyramidal; molecular structure: linear
Video \(\PageIndex{1}\): An overview of simple molecular shapes.
Molecular Structure for Multicenter Molecules
When a molecule or polyatomic ion has only one central atom, the molecular structure completely describes the shape of the molecule. Larger molecules do not have a single central atom, but are connected by a chain of interior atoms that each possess a “local” geometry. The way these local structures are oriented with respect to each other also influences the molecular shape, but such considerations are largely beyond the scope of this introductory discussion. For our purposes, we will only focus on determining the local structures.
Example \(\PageIndex{5}\): Predicting Structure in Multicenter Molecules
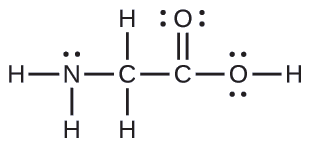
The Lewis structure for the simplest amino acid, glycine, H2NCH2CO2H, is shown here. Predict the local geometry for the nitrogen atom, the two carbon atoms, and the oxygen atom with a hydrogen atom attached:
Solution

Consider each central atom independently. The electron-pair geometries:
- nitrogen––four regions of electron density; tetrahedral
- carbon (CH2)––four regions of electron density; tetrahedral
- carbon (CO2)—three regions of electron density; trigonal planar
- oxygen (OH)—four regions of electron density; tetrahedral
The local structures:
- nitrogen––three bonds, one lone pair; trigonal pyramidal
- carbon (CH2)—four bonds, no lone pairs; tetrahedral
- carbon (CO2)—three bonds (double bond counts as one bond), no lone pairs; trigonal planar
- oxygen (OH)—two bonds, two lone pairs; bent (109°)
Exercise \(\PageIndex{5}\)
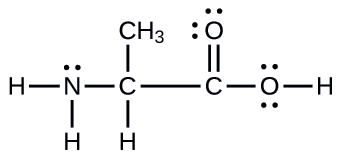
Another amino acid is alanine, which has the Lewis structure shown here. Predict the electron-pair geometry and local structure of the nitrogen atom, the three carbon atoms, and the oxygen atom with hydrogen attached:
- Answer
-
electron-pair geometries: nitrogen––tetrahedral; carbon (CH)—tetrahedral; carbon (CH3)—tetrahedral; carbon (CO2)—trigonal planar; oxygen (OH)—tetrahedral; local structures: nitrogen—trigonal pyramidal; carbon (CH)—tetrahedral; carbon (CH3)—tetrahedral; carbon (CO2)—trigonal planar; oxygen (OH)—bent (109°)
Example \(\PageIndex{6}\): Molecular Simulation
Using this molecular shape simulator allows us to control whether bond angles and/or lone pairs are displayed by checking or unchecking the boxes under “Options” on the right. We can also use the “Name” checkboxes at bottom-left to display or hide the electron pair geometry (called “electron geometry” in the simulator) and/or molecular structure (called “molecular shape” in the simulator).
Build the molecule HCN in the simulator based on the following Lewis structure:
Click on each bond type or lone pair at right to add that group to the central atom. Once you have the complete molecule, rotate it to examine the predicted molecular structure. What molecular structure is this?
Solution
The molecular structure is linear.
Exercise \(\PageIndex{6}\)
Build a more complex molecule in the simulator. Identify the electron-group geometry, molecular structure, and bond angles. Then try to find a chemical formula that would match the structure you have drawn.
- Answer
-
Answers will vary. For example, an atom with four single bonds, a double bond, and a lone pair has an octahedral electron-group geometry and a square pyramidal molecular structure. XeOF4 is a molecule that adopts this structure.
Summary
Video \(\PageIndex{2}\): What is the shape of a molecule?
VSEPR theory predicts the three-dimensional arrangement of atoms in a molecule. It states that valence electrons will assume an electron-pair geometry that minimizes repulsions between areas of high electron density (bonds and/or lone pairs). Molecular structure, which refers only to the placement of atoms in a molecule and not the electrons, is equivalent to electron-pair geometry only when there are no lone electron pairs around the central atom.
Glossary
- axial position
- location in a trigonal bipyramidal geometry in which there is another atom at a 180° angle and the equatorial positions are at a 90° angle
- bond angle
- angle between any two covalent bonds that share a common atom
- bond distance
- (also, bond length) distance between the nuclei of two bonded atoms
- bond dipole moment
- separation of charge in a bond that depends on the difference in electronegativity and the bond distance represented by partial charges or a vector
- dipole moment
- property of a molecule that describes the separation of charge determined by the sum of the individual bond moments based on the molecular structure
- electron-pair geometry
- arrangement around a central atom of all regions of electron density (bonds, lone pairs, or unpaired electrons)
- equatorial position
- one of the three positions in a trigonal bipyramidal geometry with 120° angles between them; the axial positions are located at a 90° angle
- linear
- shape in which two outside groups are placed on opposite sides of a central atom
- molecular structure
- structure that includes only the placement of the atoms in the molecule
- octahedral
- shape in which six outside groups are placed around a central atom such that a three-dimensional shape is generated with four groups forming a square and the other two forming the apex of two pyramids, one above and one below the square plane
- polar molecule
- (also, dipole) molecule with an overall dipole moment
- tetrahedral
- shape in which four outside groups are placed around a central atom such that a three-dimensional shape is generated with four corners and 109.5° angles between each pair and the central atom
- trigonal bipyramidal
- shape in which five outside groups are placed around a central atom such that three form a flat triangle with 120° angles between each pair and the central atom, and the other two form the apex of two pyramids, one above and one below the triangular plane
- trigonal planar
- shape in which three outside groups are placed in a flat triangle around a central atom with 120° angles between each pair and the central atom
- valence shell electron-pair repulsion theory (VSEPR)
- theory used to predict the bond angles in a molecule based on positioning regions of high electron density as far apart as possible to minimize electrostatic repulsion
- vector
- quantity having magnitude and direction
Contributors and Attributions
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).
- Adelaide Clark, Oregon Institute of Technology
- Fuse School, Open Educational Resource free of charge, under a Creative Commons License: Attribution-NonCommercial CC BY-NC (View License Deed: https://creativecommons.org/licenses/by-nc/4.0/)
- TED-Ed’s commitment to creating lessons worth sharing is an extension of TED’s mission of spreading great ideas. Within TED-Ed’s growing library of TED-Ed animations, you will find carefully curated educational videos, many of which represent collaborations between talented educators and animators nominated through the TED-Ed website.

